Bài tập 42 trang 128 SGK Toán 9 Tập 1

Hướng dẫn giải

a) Dùng tính chất hai tiếp tuyến cắt nhau, chứng minh tứ giác có ba góc vuông.

b) Dùng hệ thức lượng trong tam giác vuông 

c) Chứng minh \(OO'\) vuông góc với bán kính của đường tròn đường kính \(BC\) tại tiếp điểm.

d) Dùng tính chất của đường trung bình trong tam giác.

Chứng minh \(BC'\) vuông góc với bán kính của đường tròn đường kính \(OO'\) tại tiếp điểm.

Lời giải chi tiết

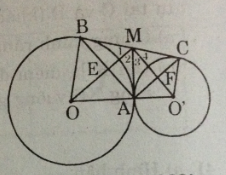
a) \(MA, MB\) là các tiếp tuyến của đường tròn (O) (gt). 

Theo tính chất của hai tiếp tuyến cắt nhau, ta có \(MA = MB\), MO là tia phân giác \(\widehat {AMB}\)

Ta có: \(∆MAB\) cân tại \(M (do\,MA = MB)\)

Có MO là đường phân giác nên MO đồng thời là đường cao

\(\Rightarrow MO \bot AB \Rightarrow \widehat {ME{\rm{A}}} = {90^0}\)

Lại có \(MA, MC\) là các tiếp tuyến của đường tròn (O') (gt). 

Theo tính chất của hai tiếp tuyến cắt nhau, ta có \(MA = MC\), MO’ là tia phân giác góc \(\widehat {AMC}\) 

Ta có: \(∆MAC\) cân tại \(M (do\,MA = MC)\)

Có MO' là đường phân giác nên MO' đồng thời là đường cao

\(\Rightarrow MO' \bot AC \Rightarrow \widehat {MFA} = 90^0\)

Vì \(MO, MO’\) là tia phân giác của hai góc kề bù \(\widehat {AMB},\widehat {AMC} \Rightarrow \widehat {EMF} = {90^0}\) (hai tia phân giác của hai góc kề bù thì vuông góc với nhau)

Tứ giác AEMF là hình chữ nhật (vì \(\widehat {EMF} = \widehat {MEA} = \widehat {MFA} = {90^0}\)  

b) \(∆MAO\) vuông tại A có AE là đường cao nên \(ME. MO = MA^2\) (hệ thức lượng trong tam giác vuông)

\(∆MAO'\) vuông tại A có AF là đường cao nên \(MF. MO’ = MA^2\) (hệ thức lượng trong tam giác vuông)

Do đó, \(ME. MO = MF. MO’ (= MA^2)\)

c) Theo câu a) ta có \(MA=MB\) và \(MA=MC\)

Suy ra \(MA = MB = MC=\dfrac{BC}2\) nên M là tâm đường tròn đường kính BC có bán kính là MA. Mà \(OO’ ⊥ MA\) tại A.

Do đó OO’ là tiếp tuyến của đường tròn đường kính BC

d)

Gọi K là trung điểm OO’, ta có K là tâm đường tròn có đường kính là OO’

Tam giác OMO' vuông tại M (do theo câu a có \(\widehat {EMF}=90^0\) hay \(\widehat {OMO'}=90^0\) ) có MK là đường trung tuyến ứng với cạnh huyền OO' nên \(KM=\dfrac{1}2OO'\) (tính chất)

Như vậy, đường tròn tâm K đường kính OO' có bán kính KM.

Ta có \(OB ⊥ BC, O’C ⊥ BC \) (do BC là tiếp tuyến) \(⇒ OB // O'C.\)

Suy ra tứ giác OBCO’ là hình thang có K, M lần lượt là trung điểm các cạnh cạnh bên OO’, BC.

Do đó KM là đường trung bình của hình thang OBCO’ \(⇒ KM // OB\)

Mà \(OB ⊥ BC\) nên \(KM ⊥ BC\)

Ta có \(BC ⊥ KM\) tại M nên BC là tiếp tuyến của đường tròn đường kính OO’. 

-- Mod Toán 9 HỌC247