Giải bài 41 tr 128 SGK Toán lớp 9 Tập 1
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O); (K) và(O); (I) và (K).
b) Tứ giác AEHF là hình gì? Vì sao?
c) Chứng minh đẳng thức \(AE.AB = AF.AC\)
d) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K)
e) Xác định vị trí của điểm H để EF có độ dài lớn nhất.
Hướng dẫn giải chi tiết
Hướng dẫn giải
a) Vị trí tương đối của hai đường tròn (O;R) và (O';r) (\(R \ge r\) )
- TH1: 2 đường tròn cắt nhau (có 2 điểm chung) khi và chỉ khi : R - r < OO' < R + r
- TH2: 2 đường tròn tiếp xúc nhau (1 điểm chung)
+) Tiếp xúc trong khi và chỉ khi OO' = R - r >0
+) Tiếp xúc ngoài khi và chỉ khi OO' = R + r
b) Chứng minh tứ giác có ba góc vuông dựa vào kiến thức : “Tiếp tuyến của đường tròn vuông góc với bán kính tại tiếp điểm."
c) Dùng hệ thức lượng về chiều cao và độ dài hình chiếu của các cạnh góc vuông lên cạnh huyền : \({h^2} = b'.c'\)
d) Chứng minh 1 đường thẳng là tiếp tuyến của 1 đường tròn thì ta chứng minh cho đường thẳng đó vuông góc với bán kính tại 1 điểm thuộc đường tròn.
e) Biểu diễn độ dài \(EF\) theo độ dài của \(AH\) rồi biện luận để tìm vị trí của dây đó vuông góc với \(BC\).
Lời giải chi tiết
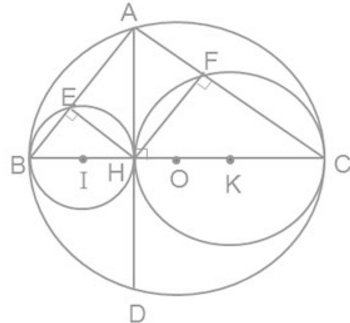
a) \(OI = OB – IB\) nên (I) tiếp xúc trong với (O)
\(OK = OC – KC\) nên (K) tiếp xúc trong với (O)
\(IK = IH + KH\) nên (I) tiếp xúc ngoài với (K)
b) Vì \(HE \bot AB\) (gt)
\( \Rightarrow \widehat {A{\rm{E}}H} = {90^0}\)
Tương tự có \(\widehat {AFH} = {90^0}\) ( do \(HF\bot AC\))
Và \(\widehat {BAC} = {90^0}\) (do A thuộc đường tròn đường kính BC)
Tứ giác AEHF có \(\widehat {EAF} = \widehat {AEH} = \widehat {AFH} = {90^0}\) nên là hình chữ nhật.
c) ∆ABH vuông tại H, HE là đường cao nên \(AH^2 = AE. AB\) (hệ thức lượng trong tam giác vuông)
∆ACH vuông tại H, HF là đường cao nên \(AH^2 = AF. AC\) (hệ thức lượng trong tam giác vuông)
Do đó \(AE. AB = AF. AC\) (vì cùng bằng \(AH^2\) )
d) Gọi M là giao điểm của AH và EF, ta có: \(ME = MF = MH = MA\) (do tứ giác AEHF là hình chữ nhật)
Xét ∆MEI và ∆MHI có:
\(ME = MH, IE = IH (=R)\), MI (cạnh chung)
Do đó \(∆MEI = ∆MHI\) (c.c.c)
\(\Rightarrow \widehat {MEI} = \widehat {MHI}\)
mà \(\widehat {MHI} = {90^0}\) (do AD vuông góc với BC) nên \(\widehat {MEI} = {90^0}\)
Suy ra \(ME \bot EI\) tại E mà IE là bán kính đường tròn (I)
⇒ ME hay EF là tiếp tuyến của đường tròn (I)
Chứng minh tương tự có EF là tiếp tuyến của đường tròn (K)
Hoặc ta chứng minh EF là tiếp tuyến của đường tròn (K) như sau:
Vì \(MF=MH\) (cmt) nên tam giác MFH cân tại M, suy ra \(\widehat {MHF}=\widehat {MFH}\) (*) (tính chất)
Vì \(KH=KF\) (= bán kính đường tròn (K)) nên tam giác KFH cân tại K.
Suy ra \(\widehat {KHF}=\widehat {KFH}\) (**) (tính chất)
Cộng theo vế với vế của (*) và (**) ta có: \(\widehat {MHF}+\widehat {KHF}=\widehat {MFH}+\widehat {HFK}\)
Hay \(\widehat {KFM}=\widehat {MHK}=90^0\) (do \(AH\bot BC\))
Suy ra \(MF\bot FK\) tại F mà KF là bán kính đường tròn (K) nên EF là tiếp tuyến của đường tròn (K)
e) Ta có \(EF = AH\) (vì AEHF là hình chữ nhật) mà \(AH ≤ AO \) (=bán kính đường tròn (O)=R)
Do đó \(EF ≤ R\), \(R\) không đổi. Dấu “=” xảy ra \(⇔ H ≡ O\)
Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.
Cách 2 câu e:
Xét đường tròn (O) có BC là đường kính và AD là dây cung mà \(AD\bot BC\) tại H nên H là trung điểm của AD (định lý). Suy ra \(AH=\dfrac{AD}2\)
Ta có \(EF = AH\) (vì AEHF là hình chữ nhật)
Suy ra \(EF=AH=\dfrac{AD}2\)
Do đó EF lớn nhất khi AD lớn nhất. Khi đó, dây AD lớn nhất là đường kính.
Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Câu hỏi 9 trang 126 SGK Toán 9 Tập 1
Câu hỏi 10 trang 126 SGK Toán 9 Tập 1
Bài tập 42 trang 128 SGK Toán 9 Tập 1
Bài tập 43 trang 128 SGK Toán 9 Tập 1
Bài tập 81 trang 171 SBT Toán 9 Tập 1
Bài tập 82 trang 171 SBT Toán 9 Tập 1
Bài tập 83 trang 171 SBT Toán 9 Tập 1
Bài tập 84 trang 171 SBT Toán 9 Tập 1
Bài tập 85 trang 172 SBT Toán 9 Tập 1
Bài tập 86 trang 172 SBT Toán 9 Tập 1
Bài tập 87 trang 172 SBT Toán 9 Tập 1
Bài tập 88 trang 172 SBT Toán 9 Tập 1
Bài tập 88 trang 172 SBT Toán 9 Tập 1
Bài tập II.1 trang 173 SBT Toán 9 Tập 1
-


Chứng minh đường tròn ngoại tiếp tam giác MNP đi qua 2 điểm cố định khi M di động biết d cắt (O) tại A và B
bởi Kiều Phương Mai
 25/04/2019
25/04/2019
Cho (O;R).đường thẳng d cắt (o) tại A và B. Từ M trên d vẽ tiếp tuyến MN và MP
a.cmr:đường tròn ngoại tiếp tamgiac MNP đi qua 2 điểm cố điịnh khi M di động
b.Xác định vị trí của M để MNOP là hình vuông.
Theo dõi (0) 0 Trả lời -


Chứng minh 25 < = x^2+y^2+u^2+v^2 < = 50 biết hình chữ nhật có hai kích thước là 3cm và 4cm
bởi na ka
 17/02/2019
17/02/2019
Cho hình chữ nhật có hai kích thước là 3cm và 4cm. Một tứ giác có 4 đỉnh nằm trên 4 cạnh của hình chữ nhật có độ dài các cạnh lần lượt là x, y, u, v. Chứng minh rằng:
Theo dõi (0) 0 Trả lời -


Cho đường tròn tâm O và dây AB của đường tròn, S là điểm chính giữa của cung nhỏ AB. Từ S vẽ hai dây SM, SN theo thứ tự cắt dây AB tại điểm P và Q.
a) Chứng minh: SP.SM = SQ.SN
b) Chứng minh: ▲SAN đồng dạng với ▲SPA
c) Chứng minh SA là tiếp tuyến tại A của đường tròn ngoại tiếp tam giác MAPTheo dõi (0) 0 Trả lời -


Cho nửa đường tròn (O) đường kính AB, trên nửa mặt phẳng bờ AB chứa nửa đường tròn đó, kẻ hai tia tiếp tuyến Ax, By với (O). Gọi (O') là đường tròn tiếp xúc với Ax tại C và tiếp xúc ngoài với nửa đường tròn (O) tại F. Kẻ tiếp tuyến CE với (O) (E là tiếp điểm, E khác A), AE cắt tia By tại D. Cho AB = 2R.
a) Tính AC.BD theo R. Chứng minh CE2 = CF.CB.
b) Đường thẳng vuông góc với By tại D cắt OE tại J, CE cắt DF tại G. Chứng minh:
- DF là tiếp tuyến của (O).
- G là tâm của đường tròn nội tiếp tam giác OIJ.
Theo dõi (0) 0 Trả lời -
ADMICRO


Cho điểm A(0,0) và điểm B(1,0). M là một điểm bất kỳ chạy trên đường tròn tâm A, bán kính AB. Tìm quỹ tích trực tâm H của tam giác ABM
Theo dõi (0) 0 Trả lời -


Chứng minh CH vuông góc với AB biết tam giác ABC có đỉnh C nằm bên ngoài đường tròn (O)
bởi Khuc Du
 07/12/2018
07/12/2018
Cho tam giác ABC có đỉnh C nằm bên ngoài đường tròn (O) tâm O đường kính AB. Biết cạnh CA cắt đường tròn (O) tại điểm D khác A, cạnh BC cắt đường tròn (O) tại điểm E khác B. Gọi H là giao điểm của AE và BD
1. Chứng minh tam giác ABD là tam giác vuông. Chứng minh CH vuông góc với AB
2. Gọi F là trung điểm của đoạn CH. Chứng minh DF là tiếp tuyến của đường tròn (O)Theo dõi (0) 1 Trả lời -


Chứng minh O là tâm đường tròn ngoại tiếp tam giác AMN biết O là tâm đường tròn nội tiếp ABC
bởi Nguyễn Thị Thu
 05/12/2018
05/12/2018
Cho tam giác ABC, gọi O là tâm đường tròn nội tiếp tam giác ABC. Trên BC lấy các điểm M và N sao cho BM=BA, CN=CA. Chứng minh O là tâm đường tròn ngoại tiếp tam giác AMN.
Theo dõi (0) 0 Trả lời -


Chứng minh DP // CQ và I, P, Q cùng thuộc 1 đường tròn biết AB, CD là 2 đường kính của (O; R)
bởi Trần Ngọc Tuân
 02/12/2018
02/12/2018
Cho AB và CD là hai đường kính của đường tròn (O; R). Qua kẻ tiếp tuyến với đường tròn (O) cắt AD và AC kéo dài lần lượt tại M và N. Gọi P, Q, H lần lượt là trung điểm của BM, BN, OB. Gọi I là giao điểm của PH và AQ.
a) CM: DP // CQ và I, P, Q cùng thuộc một đường tròn.
b) Xác định vị trí của D trên ẤM để diện tích tam giác APQ nhỏ nhất.
c) Gọi F là giao điểm của QH và AP, CM:
+
>3
Theo dõi (0) 0 Trả lời





