Giải bài 82 tr 171 SBTToán lớp 9 Tập 1
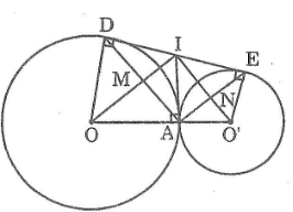
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung trong tại A cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE.
a. Tứ giác AMIN là hình gì? Vì sao?
b. Chứng minh hệ thức IM.IO = IN.IO’
c. Chứng minh rằng OO’ là tiếp tuyến của đường tròn có đường kính là DE
d. Tính độ dài DE, biết rằng OA = 5cm, O’A = 3,2cm
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
\(*\)) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
\(*\)) Tứ giác có ba góc vuông là hình chữ nhật.
\(*\)) Hệ thức lượng trong tam giác vuông:
+) Bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu cạnh góc vuông đó trên cạnh huyền.
+) Bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu hai cạnh góc vuông trên cạnh huyền.
Lời giải chi tiết
\(a)\) Trong đường tròn \((O)\) ta có \(OI\) là tia phân giác của góc \(AID\) ( tính chất hai tiếp tuyến cắt nhau IA và ID)
Trong đường tròn \((O’)\) ta có \(O’I\) là tia phân giác của góc \(AIE\) ((tính chất hai tiếp tuyến cắt nhau IA và IE)
Mà góc \(AID\) và góc \(AIE\) là hai góc kề bù nên \(IO ⊥ IO'\) ( tính chất hai góc kề bù)
Suy ra: \(\widehat {OIO'} = 90^\circ \) hay \(\widehat {MIN} = 90^\circ \)
Xét đường tròn (O) có \(IA = ID \) ((tính chất hai tiếp tuyến cắt nhau IA và ID)
Suy ra tam giác \(ADI\) cân tại \( I.\)
Tam giác \(ADI\) cân tại I có \(IO\) là phân giác của góc \(AID\) nên \(IO\) cũng là đường cao của tam giác \(AID.\)
Suy ra: \(IO ⊥ AD\) hay \(\widehat {AMI} = 90^\circ \)
Xét đường tròn (O') có \(IA = IE\) (tính chất hai tiếp tuyến cắt nhau IA và IE)
Suy ra tam giác \(AEI\) cân tại \( I.\)
Tam giác cân \(AIE\) có \(IO'\) là phân giác của góc \(AIE\) nên \(IO'\) cũng là đường cao của tam giác \(AIE.\)
Suy ra: \(IO' ⊥ AE\) hay \(\widehat {ANI} = 90^\circ \)
Tứ giác \(AMIN\) có ba góc vuông nên nó là hình chữ nhật.
\(b)\) Tam giác \(AIO\) vuông tại \(A\) có \(AM ⊥ IO.\)
Theo hệ thức lượng trong tam giác vuông \(AIO\), ta có:
\(IA^2= IM.IO \;\;\; (1)\)
Tam giác \(AIO'\) vuông tại \(A\) có \(AN ⊥ IO'.\)
Theo hệ thức lượng trong tam giác vuông \(AIO'\) , ta có:
\(IA^2= IN.IO' \;\;\; (2)\)
Từ \((1)\) và \((2)\) suy ra: \(IM.IO = IN.IO'\)
\(c)\) Ta có: \(IA = ID\) và \(IA = IE \) ( chứng minh trên) nên \(IA=ID=IE=\dfrac{DE}2\)
Suy ra \(A\) nằm trên đường tròn tâm \(I\) đường kính \(DE.\)
Vì \(OO' ⊥ IA\) tại \(A\) nên \(OO'\) là tiếp tuyến của đường tròn \(\displaystyle \left( {I;{{DE} \over 2}} \right).\)
\(d)\) Tam giác \(O'IO\) vuông tại \(I\) có \(IA ⊥ OO'.\)
Theo hệ thức lượng trong tam giác vuông \(O'IO\), ta có:
\( IA^2= OA.O'A = 5.3,2 = 16\)
Suy ra: \(IA = 4 (cm).\)
Mà \(IA=\dfrac{DE}2\Rightarrow DE = 2IA\) nên \(DE = 2.4 = 8 (cm).\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 43 trang 128 SGK Toán 9 Tập 1
Bài tập 81 trang 171 SBT Toán 9 Tập 1
Bài tập 83 trang 171 SBT Toán 9 Tập 1
Bài tập 84 trang 171 SBT Toán 9 Tập 1
Bài tập 85 trang 172 SBT Toán 9 Tập 1
Bài tập 86 trang 172 SBT Toán 9 Tập 1
Bài tập 87 trang 172 SBT Toán 9 Tập 1
Bài tập 88 trang 172 SBT Toán 9 Tập 1
Bài tập 88 trang 172 SBT Toán 9 Tập 1
Bài tập II.1 trang 173 SBT Toán 9 Tập 1
-


Tính AD, biết AB = 5cm, CD = 11cm
bởi thúy ngọc
 22/01/2019
22/01/2019
Cho hình thang cân ABCD ( AB// CD), có AC vuông góc với AD. Biết AB = 5 cm, CD = 11 cm. Tính AD
giúp mình vời mn ơi, mai mình học rồiTheo dõi (0) 1 Trả lời -


Giải tam giác ABC biết AB = 6,8 ; góc B = 50 ; góc A = 70 và tính diện tích ABC
Theo dõi (0) 1 Trả lời -


Tính cot.sin và tan^3 + cot^3
bởi Bo Bo
 22/01/2019
22/01/2019
1. Cho cot + sin = 1,2. Tính cot.sin và \(tan^3+cot^3\)
2. a) AB = 21, BC = 25, tam giác ABC vuông A. Giải tam giác
b) Tính AH đường cao, AD phân giác
Theo dõi (0) 1 Trả lời -


Tính tam giác vuông ABC, có AB = 12cm, BC = 7cm
bởi Bánh Mì
 22/01/2019
22/01/2019
Bài 1 cho tam giác ABC vuông tại C , AB = 12 cm, BC = 7 cm. Hãy tính tam giác vuông ABC
Bài 2 Cho tam giác ABC vuông tại A, sin B =0,4. Tính tỉ số lượng giác của góc C
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh A H^3 = BH . BC . CN
bởi Nguyễn Trà Long
 22/01/2019
22/01/2019
Cho \(\Delta ABC\left(\widehat{A}=90^0\right),AH\perp BC\). Gọi M và N lần lượt là hình chiếu của H trên AB và AC. Chứng minh: \(AH^3=BH.BC.CN\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng cos15^o = căn6 + căn2/4 mà không dùng bảng số, không dùng máy tính
bởi Trieu Tien
 22/01/2019
22/01/2019
CMR: \(\cos15^o=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)mà không dùng bảng số, không dùng máy tính.
Theo dõi (0) 1 Trả lời -


Tính BH, AH, góc C có góc B=60°, AB=8
bởi Nguyễn Minh Hải
 22/01/2019
22/01/2019
Cho tam giác ABC vuôbg tại A có góc B=60°,AB=8. Đường cao AH
a) tính BH , AH , góc C
b) phân giác góc A cắt BC tại E. Tính BE, CE
c) kẻ trung tuyến AM của tam giác ABC. Tính diện tích tam giác AHM
Giúp em nhanh vs ạ
Theo dõi (0) 1 Trả lời -


Rút gọn các biểu thứcsin40^o- cos50^o
bởi khanh nguyen
 22/01/2019
22/01/2019
1. Rút gọn các biểu thức:
a) \(\sin40^o-\cos50^o\)
b) \(\sin^230^o+\sin^240^o+\sin^250^o+\sin^260^o\)
Theo dõi (0) 1 Trả lời





