Giải bài 88 tr 172 SBTToán lớp 9 Tập 1
Cho nửa đường tròn tâm \(O\) có đường kính \(AB.\) Gọi \(M\) là điểm bất kì thuộc nửa đường tròn, \(H\) là chân đường vuông góc kẻ từ \(M\) đến \(AB.\) Vẽ đường tròn \((M ; MH).\) Kẻ các tiếp tuyến \(AC, BD\) với đường tròn tâm \(M ( C\) và \(D\) là các tiếp điểm khác \(H).\)
\(a)\) Chứng minh rằng ba điểm \(C, M, D\) thẳng hàng và \(CD\) là tiếp tuyến của đường tròn \((O).\)
\(b)\) Chứng minh rằng khi điểm \(M\) di chuyển trên nửa đường tròn \((O)\) thì tổng \(AC + BD\) không đổi.
\(c)\) Giả sử \(CD\) và \(AB\) cắt nhau tại \(I.\) Chứng minh rằng tích \(OH.OI\) không đổi.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
\(*\)) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
+) Điểm đó cách đều hai tiếp điểm.
+) Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
\(*\)) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
\(*\)) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy.
\(*\)) Hệ thức lượng trong tam giác vuông: Bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu cạnh góc vuông đó trên cạnh huyền.
Lời giải chi tiết
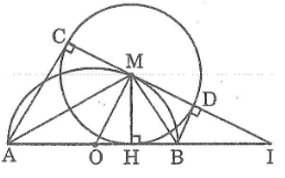
\(a)\) Trong đường tròn \((M; MH),\) có AC và AH là 2 tiếp tuyến cắt nhau tại A, theo tính chất hai tiếp tuyến cắt nhau, ta có: \( MA\) là tia phân giác của góc \(HMC\) và \(AC=AH\)
Suy ra: \(\widehat {CMA} = \widehat {HMA}\) hay \(\widehat {CMH} = 2\widehat {HMA}\)
Trong đường tròn \((M; MH),\) có BD và BH là 2 tiếp tuyến cắt nhau tại B, theo tính chất hai tiếp tuyến cắt nhau, ta có: \(MB\) là tia phân giác của góc \(HMD\) và \(BD=BH\)
Suy ra: \(\widehat {HMB} = \widehat {DMB}\) hay \(\widehat {DMH} = 2\widehat {HMB}\)
Tam giác \(ABM\) nội tiếp đường tròn \((O)\) có \(AB\) là đường kính nên vuông tại \(M\)
Suy ra: \(\widehat {AMB} = 90^\circ \) hay \(\widehat {HMA} + \widehat {HMB} = 90^\circ \)
Suy ra: \(\widehat {CMH} + \widehat {HMD} = 2\widehat {HMA} + 2\widehat {HMB}\)
\(= 2 (\widehat {HMA} + \widehat {HMB}) = 2.90^\circ = 180^\circ \)
Vậy \(C, M, D\) thẳng hàng.
\(b)\) Theo câu a) ta có: \(AC = AH\) và \(BD = BH\)
Khi \(M\) thay đổi trên nửa đường tròn tâm \(O\) thì \(AC\) luôn bằng \(AH\) và \(BD\) luôn bằng \(BH.\)
Suy ra: \(AC + BD = AH + BH = AB\) không đổi
\(c)\) Ta có: \(AC ⊥ CD \) và \( BD ⊥ CD\) ( tính chất tiếp tuyến)
Suy ra: \(AC // BD\) hay tứ giác \(ABDC\) là hình thang
Mà \(OA = OB \) (= bán kính \((O)\))
Và \(MC = MD\) (= bán kính \((M)\))
Suy ra \(OM\) là đường trung bình của hình thang \(ABCD\)
Khi đó \(OM // AC.\) Suy ra: \(OM ⊥ CD\) hay \(\widehat {OMI} = 90^\circ \)
Tam giác \(OMI\) vuông tại \(M\) có \(MH ⊥ OI.\)
Theo hệ thức lượng trong tam giác vuông, ta có: \(OM^2= OH.OI\)
Mà OM là bán kính đường tròn (O) nên OM có độ dài không đổi.
Suy ra: \(OH.OI \) không đổi.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Tính AB, AC, BC, biết AH=12cm, BH = 9cm
bởi thu thủy
 28/01/2019
28/01/2019
Cho tam giác vuông ABC đường cao AH . Biết AH ::: 12cm, BH ::: 9cm
a) Tính AB , AC , BC
b) Tính diện tích tam giác ABC
Theo dõi (0) 1 Trả lời -


Chứng minh a/sinA=b/sinB=c/sinC
bởi Lê Minh Hải
 28/01/2019
28/01/2019
Cho tam giác ABC nhọn có AB =c ,AC =b ,BC .
Chứng minh : a)
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}.\)
b)\(S_{ABC}=\dfrac{1}{2}absinC=\dfrac{1}{2}bcsinA=\dfrac{1}{2}acsinB\)
Theo dõi (0) 1 Trả lời -


Chứng minh 1/AE^2+1/AF^2=1/a^2
bởi Lê Thánh Tông
 28/01/2019
28/01/2019
Qua đỉnh A của hình vuông ABCD cạnh bằng a, vẽ 1 đường thẳng cắt BC ở E và cắt DC ở P.
Chứng minh: \(\dfrac{1}{AE^2}+\dfrac{1}{AF^2}=\dfrac{1}{a^2}\)
Theo dõi (0) 1 Trả lời -


Tính AH, AB, AC, góc B, biết BH=4cm, CH=9cm
bởi Hy Vũ
 28/01/2019
28/01/2019
Cho \(\Delta ABC\) vuông tại A, đường cao AH.
a. Biết BH=4cm, CH=9cm. Tính AH, AB, AC, \(\widehat{B}\).
b. Vẽ HM, HN vuông góc với AB, AC. Chứng minh AM.AB=AN.AC
c. Đường thẳng vuông góc với BC tại B cắt AC tại E. Chứng minh BH.BC=AE.AC
d. Chứng minh \(\dfrac{BM}{CN}=\dfrac{AB^3}{AC^3}\).
________giúp e phần d với___________________
Theo dõi (0) 1 Trả lời -
ADMICRO


Tính BC, có AB = 16cm, AC = 14cm, B = 60 độ
bởi Tram Anh
 26/01/2019
26/01/2019
bài 1 : cho tam giác ABC có AB = 16cm , AC = 14cm . B = 60 độ .
a, tính BC
b, diện tích ABC = ?
bài 2 :cho tam giác ABC vuông tại A , AC= 15cm , B = 50 độ
tính độ dài
a, AB , B C
b, pg CD
Theo dõi (0) 1 Trả lời -


Giải tam giác ABC vuông tại A, biết BC =5cm, góc C=62 độ
bởi Mai Đào
 26/01/2019
26/01/2019
Gỉai tam giác ABC vuông tại A ,biết:
a)BC =5cm ,góc C=62 độ.
b)AB =4cm ,AC =6cm.
Theo dõi (0) 1 Trả lời -


Tính A= tan 2 α + cot 2 α, cho tan α + cot α = 2
bởi Nguyễn Thị Thanh
 26/01/2019
26/01/2019
Bài 1
Cho \(\tan\alpha+\cot\alpha=2\). Tính A= \(\tan^2\alpha+\cot^2\alpha\)
Bài 2
Cho \(\Delta ABC,\widehat{B}=30^0,\widehat{C}=45^0\), AB=8cm. Tính AC(làm tròn đến chữ số thập phân thứ nhất)
Bài 3
Cho \(\Delta ABC\), đường cao AH(\(H\in BC\)). Từ H kẻ \(HM\perp AB\left(M\in AB\right)\); \(HN\perp AC\left(N\in AC\right)\). Chứng minh: AM.AB = AN.AC
Theo dõi (0) 1 Trả lời -


Cho hình thang ABCD ( AB//CD ) . AB = 4cm , CD = 14CM , AD = 6cm , BC = 8cm . Tính SABCD
Theo dõi (0) 1 Trả lời





