Giải bài 74 tr 147 sách BT Toán lớp 7 Tập 1
Tính số đo các góc của tam giác \(ACD\) như hình 60.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Trong tam giác vuông hai góc nhọn phụ nhau.
- Góc ngoài tam giác bằng tổng hai góc trong không kề với nó.
Lời giải chi tiết
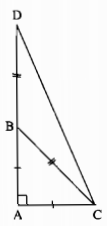
Tam giác \(ADC\) vuông tại \(A\) nên \(\widehat {DAC}=90^0\)
\( ∆ABC\) vuông cân tại \(A\)
\( \Rightarrow \widehat {ABC} = \widehat {ACB} \) (tính chất tam giác cân) và \( \widehat {ABC} + \widehat {ACB}=90^o \) (trong tam giác vuông hai góc nhọn phụ nhau).
\( \Rightarrow \widehat {ABC} = \widehat {ACB} = 45^\circ \).
Lại có \(BC = BD\) (gt) \(\Rightarrow ∆BCD\) cân tại \(B \).
\(\Rightarrow \widehat {BC{\rm{D}}} = \widehat D\) (tính chất tam giác cân)
Xét \(∆BCD\) có \(\widehat {ABC}\) là góc ngoài tại đỉnh \(B\).
Do đó \(\widehat {ABC} = \widehat {BC{\rm{D}}} + \widehat D\) (tính chất góc ngoài của tam giác)
\(\Rightarrow \widehat {ABC} = 2\widehat {BC{\rm{D}}}\)
\(\displaystyle \Rightarrow \widehat {BC{\rm{D}}} = {{\widehat {ABC} } \over 2}\)
\(\displaystyle \Rightarrow \widehat {BC{\rm{D}}} = {{45^\circ } \over 2} = 22^\circ 30'\)
Vậy \(\widehat {AC{\rm{D}}} = \widehat {ACB} + \widehat {BC{\rm{D}}} = 45^\circ + 22^\circ 30' \)\(\,= 67^\circ 30'\)
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Bài tập 72 trang 147 SBT Toán 7 Tập 1
Bài tập 73 trang 147 SBT Toán 7 Tập 1
Bài tập 75 trang 147 SBT Toán 7 Tập 1
Bài tập 76 trang 147 SBT Toán 7 Tập 1
Bài tập 77 trang 148 SBT Toán 7 Tập 1
Bài tập 78 trang 148 SBT Toán 7 Tập 1
Bài tập 79 trang 148 SBT Toán 7 Tập 1
-


Cung cung tròn tâm A có bán kính 9cm có cắt đường thẳng BC không biết ABC cân tại A?
bởi Hương Lan
 12/04/2019
12/04/2019
Cho tam giác ABC cân tại A có AB=AC=10cm ,BC=12cm .Vẽ cung tròn tâm A có bán kính 9cm .Cung đó có cắt đường thẳng BC hay không ,có cắt cạnh BC hay không ?Vì sao?
Theo dõi (0) 1 Trả lời -


Vì sao các góc ở đáy của tam giác cân là góc nhọn ?
bởi thu hằng
 12/04/2019
12/04/2019
trong tam giác cân,vì sao mỗi góc ở đáy lại là góc nhọn
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A có góc A bằng 800. Vẽ các tam giác đều BAD và CAE ra ngoài tam giác ABC. Tính Số đó góc ADE.
P/s:nhớ ghi cách giải nhé!
Ai đúng thì mik tick luôn!!!

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác DCE cân biết tam giác ABC vuông tại A có AB=9cm, AC=12cm
bởi Nguyễn Thủy
 12/04/2019
12/04/2019
Đ4.6 /Cho \(\Delta ABC\) vuông tại A, biết AB= 9cm, AC= 12cm
a. Tính BC
b. Tia phân giác của góc B cắt cạnh AC tại D. Vẽ DM vuông góc BC tại M. Chứng minh \(\Delta DBA=\Delta DBM\) suy ra \(\Delta ABM\) cân
c. Gọi E là giao điểm DM và AB. C/m AM // EC và \(\Delta DCE\) cân
d. Vẽ CH vuông góc với DB tại H. C/m 3 điểm C,H,E thẳng hàng
Làm câu c,d thôi ạ, câu a,b em đã giải rồi ko cần làm đâu ạ..E tks nhìu
Theo dõi (0) 1 Trả lời -
ADMICRO


Bai: Cho tam giác ABC vuông tại A, có góc C = 30*, kẻ đường vuông góc AH (H thuộc BC).Trên đoạn HC lấy điểm D sao cho HD = HB.Kẻ CE vuông góc với đường thẳng AD tại E.CM:
a) tam giác ABD là tam giác đều
b) tam giác ADC cân và AH = CE
c) EH // AC
Theo dõi (0) 1 Trả lời -


Cho tam giác đều ABC. Lấy các điểm D,E,F theo thứ tự thuộc các cạnh AB,BC,CA sao cho AD=BE=CF.Chứng minh rằng \(\Delta\)DEF là tam giác đều
Theo dõi (0) 1 Trả lời -


cho tam giác vuông tại A, phân giác góc B cắt AC tại H, kẻ HE vuông góc với BC, EA cắt BH tại I
a) chứng minh tam giác ABH= tam giác EBH
b) chứng minh BH là trung trực của AE
c) cho EH vuông góc với IC, tam giác IBC là tam giác gì?
Theo dõi (0) 1 Trả lời -


Tính DG biết tam giác ABC cân tại A có AB=13cm, BC=10cm
bởi A La
 12/04/2019
12/04/2019
cho tam giác ABC cân tại A có AD là đường phân giác
a) chứng minh ta giác ABD = tam giác ACD
b) gọi G là trọng tâm tam giác ABC , chứng mình 3 điểm A,G,D thẳng hàng
c) tính DG biết AB=13cm,BC=10cm
Theo dõi (0) 1 Trả lời -


cho tam giác abc cân tại a có ab=10; bc=12. Hạ ah vuông góc bc tại h.
- chứng minh tam giác abh = ach (không cần)
- tính độ dài ah (không cần)
- Kẻ hm vuông góc ab tại m, hn vuông góc ac tại n. chứng minh tam giác amn cân (cần)
help me!!!
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho \(\Delta ABC\)
\(\widehat{A}=2\widehat{B}.\)
Chứng minh: \(BC^2=AC^2+AB.AC\)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có AB<AC. Gọi M là trung điểm của BC , từ M kẻ đường thẳng vuông góc với tia phân giác của góc BAC tại N và cắt AB tại E và cắt AC tại F. CMR:
a) AE=AFb) BE=CF
c) AE=\(\dfrac{AB+AC}{2}\)
Giúp mk với
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác IKC cân biết tam giác ABC vuông tại A có tia phân giác góc B cắt AC
bởi Lê Minh Trí
 16/04/2019
16/04/2019
Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại I. Vẽ IH vuông góc với BC( H thuộc BC). GỌi K là giao điểm của IH và AB
a. CM IA=IH
b. Cm tam giác IKC cân
c. Cho BH=6cm, HC=4 cm. Tính AB và AC
d. Cm IB+IK+IC >\(\dfrac{BK+KC+CB}{2}\)
Theo dõi (0) 1 Trả lời -


Tính AM=BC biết tam giác ABC cân tại A có góc A=20 độ, tam giác DBC đều
bởi Trần Phương Khanh
 16/04/2019
16/04/2019
Cho tam giác ABC cân tại A có góc A = 20o. Vẽ tam giác đều DBC, D nằm trong tam giác ABC, Tia phân giác của góc ABD cắt AC tại M. C/m:
a/ Tia AB là phân giác của góc BAC
b/ AM = BC
Theo dõi (0) 1 Trả lời -


cho tam giác ABC cân tại A.vẽ tam giác ABD đều và tam giác ABE vuông cân tại A.gọi O là giao điểm của BE và CD.tính góc BOC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A có \(\widehat{A}=80^0\). Trên BC lấy điểm I sao cho \(\widehat{BAI}=50^0\). Trên AC lấy điểm K sao cho \(\widehat{ABK}=30^0\). 2 đoạn AI và BC cắt nhau tại H. CMR: \(\Delta HIK\) cân.
Theo dõi (0) 1 Trả lời -


Chứng minh CK vuông góc AB biết tam giác ABC cân tại A có BH vuông góc AC
bởi Trần Phương Khanh
 16/04/2019
16/04/2019
Tam giác ABC cân tại A, BH \(\perp \) AC (H \(\in\) AC), HK // BC (K \(\in\) AB). CMR : CK \(\perp\) AB
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân
a) Có 1 góc bằng 100 độ, góc đó là góc nào? Tính các góc còn lại.
b) Có 1 góc bằng 50 độ. Tính các góc còn lại.
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vuông tại A(AB<AC), trên tia đối của tia AB lấy điểm D sao cho AD=AB\
a) So sánh các góc của tam giác ABC
b) Chứng minh rằng: tam giác CBD cân
c) Gọi M là trung điểm của CD . Đường thẳng đi qua D và song song vớ BC cắt đường thẳng BM tại E. CMR: BC+BD> BE
d) Gọi K là giao điểm của AE và DM. CMR: BC=3DK
Theo dõi (0) 1 Trả lời -


Cho mk hoi:Tại sao 2 mái kèo của mái nhà thường tạo thành tam giác cân?????????(Toan 7)
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác IDC cân tại D biết tam giác ABC vuông tại A có BD là phân giác
bởi Hoa Hong
 16/04/2019
16/04/2019
cho tam giác ABC vuông tại A, có BD là phân giác (D \(\in\) AC) . Từ D kẻ DH vuông góc với BC (H \(\in\) BC)
a) Chứng minh \(\Delta\) ABD = \(\Delta\) HBD
b) So sánh DA và DC
c) gọi I là giao điểm của hai đường thẳng BA và HD. Chứng minh \(\Delta\) ADI =\(\Delta\) HDI
d) Chứng minh \(\Delta\) IDC cân tại D
Theo dõi (0) 1 Trả lời -


Chứng minh AB=AC hoặc góc A=60 độ biết tam giác ABC có 2 đường phân giác trong BD, CE
bởi Phạm Hoàng Thị Trà Giang
 16/04/2019
16/04/2019
Cho tam giác ABC có 2 đường phân giác trong BD, CE cắt nhai tại I, ID=IE. CMR: hoặc AB=AC hoặc góc A = 60 độ
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A. LẤy điểm I nằm trong tam giác sao cho góc IAC=ICA=150. Tính góc AIB
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân có AB=AC=5cm.Kẻ AH vuông góc với BC ( H thuộc BC).
a, Chứng minh HB=HC và BAC=CAH
b, Tính độ dài BH biết AH=4cm.
c, Kẻ HD vuông góc với AB(D thuộc AB), kẻ HE vuông góc với AC ( E thuộc AC). tam giác ADE LÀ TAM GIÁC GÌ, VÌ SAO
Theo dõi (0) 1 Trả lời -


Chứng minh AB=AC+DB biết đoạn thẳng CD có trung điểm là M
bởi na na
 16/04/2019
16/04/2019
cho đoạn thẳng CD có trung điểm là M trên cùng một nữa mặt phẳng bờ CD vẽ các tia CX,DY cùng cuông góc với CD.lấy điểm A bết kì trên CX(AFC) qua M vẽ đường thẳng vuông góc với MA cắt tia DY tại B cắt tia AC tại E .chứng minh
a)tam giác CME=tam giác DMB
b)tam giác ABE cân
c)AB=AC+DB
Theo dõi (0) 1 Trả lời -


Cho tam giác có góc A = 90 độ , AC>AB . Kẻ AH vuông góc với BC . Trên BC lấy điểm D sao cho HD=HB . Kẻ CE vuông góc với AD kéo dài . Chứng minh rằng :
a) Tam giác BAD cân
b) CD là phân giác của góc ACE
c) Gọi giao điểm của AH và CE là K . Chứng minh : KD song song với AB .
d) Tìm điều kiện của tam giác ABC để tam giác AKC đều .
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác MHK cân biết tam giác ABC vuông cân ở A có M là trung điểm BC
bởi Ngoc Nga
 16/04/2019
16/04/2019
Cho tam giác ABC vuông cân ở A. Điểm M là trung điểm của BC. Điểm E nằm giữa M và C. Kẻ BH vuông góc với AE, CK vuông góc với AE. Chứng minh rằng: a, BH = AE
b, Tam giác MBH = Tam giác MAK
c, Tam giác MHK cân
Theo dõi (0) 1 Trả lời -


Tìm điều kiện của tam giác ABC để góc IED = 30 độ biết tam giác ABC cân tại A có góc A nhọn
bởi Lê Tấn Thanh
 16/04/2019
16/04/2019
Bài 1: Cho tam giác ABC cân tại A, góc A nhọn. Kẻ tia Bx vuông góc AB cắt tia AC tại D; tia Cy vuông góc AC cắt ia AB tại E. Gọi giao điểm của 2 tia Bx và Cy là I. CMR: a, AD=AE; BD=CE b, Tam giác EID cânn, góc BAI=IAC c, BC//ED; AI vuông góc ED d, Tìm ĐK của tam giác ABC để góc IED = 30 độ ( giúp miifnh vs , thank nhiều)
Theo dõi (0) 1 Trả lời -


Chứng minh AI vuông góc với DE biết tam giác ABC cân tại A, trên AB và AC lấy điểm D và E
bởi Lan Anh
 16/04/2019
16/04/2019
Cho tam giác ABC cân tại A . Trên AB và AC lấy điểm D và E sao cho BD=CE.gọi I là trung điểm của BC.Chứng minh AI vuông góc với DE.
Theo dõi (0) 1 Trả lời -


cho tam giác ABC cân tại A, đường trung trực tuyến AM. đường trung trực của AC cắt đường thẳng AM ở D. chứng minh rằng DA=DB
Theo dõi (0) 1 Trả lời -


Cho ΔABC vuông tại A, đường cao AH. Kẻ AE là tia phấn giác của góc BAH, AF là tia phân giác của góc CAH. Chứng minh rằng AB + AC = BC + EF.
Theo dõi (0) 1 Trả lời -


Chứng minh AI vuông góc với DE biết tam giác ABC cân tại A có I là trung điểm BC
bởi Nguyễn Lệ Diễm
 16/04/2019
16/04/2019
cho tam giác abc cân tại a . trên ab và ac lấy điểm d và e sao cho bd=ce.gọi i là trung điểm của bc,cm ai vuông góc với de
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABC cân biết tam giác ABC có góc B=5-0 độ, từ đỉnh A kẻ đường thẳng
bởi Lê Minh
 16/04/2019
16/04/2019
Bài 1: Cho tam giác ABC có góc B=50 độ. Từ đỉnh A kẻ đường thẳng song song với BC cắt tia phân giác của góc B ở E.
a/ CM: Tam giác ABC cân.
b/ Tính góc BAE.
Bài 2: Cho tam giác cân ABC (AB=AC). Trên các cạnh AB và AC lấy tương ứng 2 điểm D và E sao cho AD=AE. Gọi M là trung điểm của BC. CMR:
a/ DE song song BC
b/ Tam giác MBD=tam giác MCE
c/ Tam giác AMD=tam giác AME
Theo dõi (0) 1 Trả lời -


Cho tam giac ABC vuong tai A, goc C=30do. Duong cao AH. Tren canh HC lay diem D sao cho HD=HB. Tu C keo CE vuong goc AD. Cm. a, Tam giac ABD deu. b, EH song song AC
Theo dõi (0) 1 Trả lời -


cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở Ổ. qua O kẻ đường thẳng song song với BC cắt AB ở M, cắt AC ở N. chứng minh: MN= BM+CN
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABC cân biết tam giác ABC có các phân giác BE và CF cắt nhau tại I
bởi Nguyễn Hạ Lan
 16/04/2019
16/04/2019
Cho Tam giác ABC có các đường phân giác BE và CF cắt nhau tại I. Biết AE=AF. CMR : Tam giác ABC là Tam giác cân
Theo dõi (0) 1 Trả lời -


Cho ΔABC cân tại A. Trên cạnh BC lấy D, trên tia đối của CA lấy E sao cho BD = CE. Kẻ DM // AC. I là trung điểm của MC.
a) Chứng minh D, I, E thẳng hàng
b) Kẻ DH và CK cùng vuông góc với BC. Chứng minh BH = CK (H, K thuộc BC)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A có góc A=800
a) tính góc B,C
B)Các tia phân giác BDvàCE CẮT NHAU ở O.CMR:BE=ED=DC
c)c/m: tam giác OAE=tam giác OAD
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AMN cân biết tam giác ABC cân tại A, trên tia đối của tia BA lấy D
bởi hi hi
 16/04/2019
16/04/2019
Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy D, trên tia đối của tia CA lấy E sao cho BD=CE
a) Chứng minh rằng: DE // BC.
b) Từ D kẻ DM vuông góc với BC tại M, từ E kẻ EN vuông góc với BC tại N. Chứng minh rằng: DM=EN.
c) Chứng minh rằng: AMN là tam giác cân.
d) Từ B và C kẻ các đường vuông góc với AN và AM, chúng cắt nhau tại I. Chứng minh rằng: AI là tia phân giác của góc BAC.
Các bạn giúp mình nhé.
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác BOC cân biết tam giác ABC cân tại A có O là trung điểm BM và CN
bởi Thu Hang
 16/04/2019
16/04/2019
cho tam giác ABC cân tại A. Gọi M là trung điểm của AC, N là trung điểm của AB.
a) chứng minh BM= CN
b) gọi O là trung điểm của BM và CN.
chứng minh tam giác BOC cân.
Theo dõi (0) 1 Trả lời -


Phương pháp chứng minh 1 tam giác là tam giác cân
bởi hoàng duy
 16/04/2019
16/04/2019
cách chứng minh các tam giác là tam giác cân
Theo dõi (0) 1 Trả lời -


Cho tan giác ABC vuông tại A, đường cao AH, trên tia HC lấy điểm D sao cho HD=HB
a/ Tam giác ABD là tam giác gì? Vì sao? Nếu góc C=30 độ thì tam giác ABD là tam giác gì? Vì sao?
b/ Từ C vẽ đường thẳng vuông với tia AD tại M. Chứng minh CB là tia p/g của góc ACM
c/ Tia AH cắt CM tại Q. CM tam giác ACQ cân
d/Chứng minh QD vuông góc với AC
Theo dõi (0) 1 Trả lời -


Cho tg MNP cân tại M có MH là đường phân giác.
a) C/m tg MNH=MPH
b) Gọi G là trọng tâm của tg MNP. c/m 3 điểm M,N,P thẳng hàng
c) Tính HG biết MN=13cm và đoạn NP=10cm
giúp mk giải bài toán này với mai mk kiểm tra rồi!!!
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


So sánh góc DBC và góc DCB biết tam giác ABC cân tại A có các phân giác góc B và C cắt tại D
bởi Lê Nguyễn Hạ Anh
 16/04/2019
16/04/2019
Nhờ các bạn giúp đỡ. Mình cần rất gấp. Cảm ơn nhiều!
Cho hình bên: ( bài Ca/ bài 8/ hình 7 sách VNEN )
a) CM: tam giác ABD = tam giác ACD
b) So sánh góc DBC và góc DCB
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác MAB cân biết tam giác ABC có BC=2AB, M là trung điểm của BC
bởi sap sua
 16/04/2019
16/04/2019
Cho tam giác ABC có BC = 2AB . Gọi M là trung điểm của BC , N là trung điểm của BM . Trên tia đối của tia NA lấy điểm E sao cho AN = EN . Chứng Minh :
a) Tam giác NAB = Tam giác NEMb) Tam Giác MAB là tam giác cân
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có AB=AC=5cm , BC=8cm.Kẻ AH vuông góc với AC (E thuộc AC).
a) Chứng minh : HB=HC và góc BAH = góc CAH
b)Tính độ dài AH
c) Kẻ AH vuông góc với AB (D thuộc AB),kẻ HE vuông góc với AC (E thuộc AC ) . Chứng minh tam giác HDE là tam giác cân
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho AM+AN=2AB
a) Chứng minh BM=CN
b) Chứng minh BC đi qua trung điểm của đoạn thẳng MN
c) Đường trung trực của MN và tia phân giác của góc BAC cắt nhau tại K. Chứng minh KCvuông gócAC
Theo dõi (0) 1 Trả lời -


Chứng minh BH vuông góc CN biết tam giác ABC có góc A=90 độ, đường phân giác BH
bởi Bo bo
 16/04/2019
16/04/2019
Cho tam giác ABC có góc A bằng 90 độ,đường phân giác BH (H thuộc AC) kẻ HM vuông góc với BC.Gọi N là giao điểm của AB và MH.CMR
a, Tam giác ABH bằng tam giác MBH
b,BH là đường trung trực của đoạn thẳng AM
c,AM song song CN
d,BH vuông góc với CN
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AMN đều biết M và N lần lượt là trung điểm của CD và BE
bởi Việt Long
 16/04/2019
16/04/2019
Cho tam giác ABC nhọn (AB<AC). Vẽ ra phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi I là giao điểm của CD và BE, K là giao điểm của AB và DC.
a) Chứng minh rằng: tam giác ADC bằng tam giác ABE.
b) Gọi M và N lần lượt là trung điểm của CD và BE. Chứng minh tam giác AMN đều.
Các bạn chỉ cần giúp mình phần b thui, phần a mình làm được rùi, không cần vẽ hình nha!!!!!!!
Theo dõi (0) 1 Trả lời -


Chứng minh AM là tia phân giác của góc BAC biết tam giác ABC cân tại A có M là trung điểm BC
bởi thu trang
 16/04/2019
16/04/2019
cho tam giác ABC cân tại A ,M là trung điểm của BC .Trên tia đối của tia MA lấy điểm D sao cho AM=MD chứng minh rằng
a) tam giác ABM=DCM
b) AB//DC
c) AM vuong
d) AM là tia phân giác của góc BAC
Theo dõi (0) 1 Trả lời -


Chứng minh BI=CK biết tam giác ABC cân tại A có góc A < 90 độ, BI vuông góc AC
bởi Đào Lê Hương Quỳnh
 17/04/2019
17/04/2019
cho tam giác ABC ( cân tại góc A (A<90 độ)kẻ BI vuông góc vs AC ( I thuộc AC) CK vuông góc AB ( K thuộc AB)
Chứng MInh
a,BI=CK
b, tam giác AKI cân tại A
c,cho BI=5cm,AC=8cm,AI=6cm.Tính chu vi tam giác BKC (làm tròn đến chữ sô thập phân thứ nhât)
Theo dõi (0) 1 Trả lời


