Giải bài 56 tr 145 sách BT Toán lớp 7 Tập 1
Cho hình dưới, chứng minh rằng O là trung điểm của mỗi đoạn thẳng AD, BC
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
- Nếu đường thẳng \(c\) cắt hai đường thẳng \(a, b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc cặp góc đồng vị bằng nhau, hoặc cặp góc trong cùng phía bù nhau) thì \(a\) và \(b\) song song với nhau.
Lời giải chi tiết
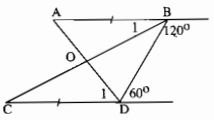
Hai đường thẳng AB và CD tạo với BD có hai góc trong cùng phía bù nhau
\(120^\circ + 60^\circ = 180^\circ \)
Suy ra AB // CD
Ta có: \(\widehat A = \widehat {{D_1}}\) (hai góc trong so le)
\(\widehat {{B_1}} = \widehat C\) (hai góc trong so le)
AB = CD (gt)
Suy ra: ∆AOB = ∆DOC (g.c.g)
Suy ra: OA = OD; OB = OC (hai cạnh tương ứng)
Vậy O là trung điểm của mỗi đoạn thẳng AD và BC.
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Bài tập 54 trang 144 SBT Toán 7 Tập 1
Bài tập 55 trang 145 SBT Toán 7 Tập 1
Bài tập 57 trang 145 SBT Toán 7 Tập 1
Bài tập 57 trang 145 SBT Toán 7 Tập 1
Bài tập 59 trang 145 SBT Toán 7 Tập 1
Bài tập 60 trang 145 SBT Toán 7 Tập 1
Bài tập 61 trang 145 SBT Toán 7 Tập 1
Bài tập 62 trang 145 SBT Toán 7 Tập 1
Bài tập 63 trang 146 SBT Toán 7 Tập 1
Bài tập 64 trang 146 SBT Toán 7 Tập 1
-


Chứng minh BD song song AM biết tam giác ABC có M là trung điểm BC, I là trung điểm AB
bởi Nguyễn Thanh Hà
 10/04/2019
10/04/2019
Cho tam giác ABC , M là trung điểm của BC, I là trung điểm của AB. Từ A kẻ AD song song BM / AD = BM, B và M nằm khác phía so với AD.
a) Chứng minh tam giác DAB = tam giác MBA
b) Chứng minh DI = IM ; M I O thẳng hàng
c) Chứng minh BD song song AM
GIÚP MỊ VỚI MỊ CẦN GẤP LẮM LUÔN Ý !!!
 GIÚP MỊ NHA !!! TKS NHÌU
GIÚP MỊ NHA !!! TKS NHÌU  Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC. Đường thẳng đi qua B song song với AC, đường thẳng đi qua C song song với AB. Chúng cắt nhau tại D và cắt đuòng thẳng qua đỉnh A song song với BC theo thứ tự tại E và F.
a, CM: tam giác ABC=tam giác ABE
b, Tính chu vi tam giác DEF biết chu vi tam giác ABC=15
Theo dõi (0) 1 Trả lời -


Chứng minh CM=RS biết tam giác ABC vuông cân có góc C=90 độ, M thuộc AB, MR vuông góc AC
bởi Bin Nguyễn
 10/04/2019
10/04/2019
Cho tam giác ABC vuông cân, góc C = 90 độ, M \(\in\) AB, kẻ MR \(\perp\) AC, MS \(\perp\) BC
a) Chứng minh: CM và RS = nhau và cắt nhau tại trung điểm mỗi đoạn
b) Gọi O trung điểm của AB. Hỏi tam giác ORS là tam giác gì ?
Theo dõi (0) 1 Trả lời -


Chứng minh CD=AC+BD biết C là một điểm thuộc tia Ax, đường vuông góc với OC tại O
bởi Bo Bo
 10/04/2019
10/04/2019
Cho đoạn thẳng AB, O là trung điểm của đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia Ax và By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường vuông góc với OC tại O cắt tia By ở D. Chứng minh rằng: CD=AC+BD
Các bạn ơi! Giúp mk với


 !Theo dõi (0) 1 Trả lời
!Theo dõi (0) 1 Trả lời -
ADMICRO


cho tam giác ABC qua A kẻ đường thẳng song song với BC qua C kẻ đường thẳng song song với AB, 2 đường thẳng cắt nhau tại D.
Chứng minh: tam giác ABC=tam giác ADC
Chứng minh: tam giác ADB=CBD
AC giao BD.Chứng minh: tam giác ABO=tam giác COD
Vẽ hình
Theo dõi (0) 1 Trả lời -


Chứng minh AC=BD biết góc OAC=góc OBD và OA=OB
bởi Thanh Truc
 22/02/2019
22/02/2019
Chứng Minh AC=BD
Theo dõi (0) 1 Trả lời -


Chứng minh EG+FH=AB biết trên cạnh BC của tam giác ABC, lấy các điểm E và F
bởi Nguyễn Trà Giang
 11/04/2019
11/04/2019
Trên cạnh BC của tam giác ABC, lấy các điểm E và F sao cho BE=CF. Qua E và F, vẽ các đường thẳng song song với BA, chúng cắt cạnh AC theo thứ tự ở G và H. CMR: EG+FH=AB
Các bạn giúp mk với
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh AD=BC biết tam giác ABC vuông ở C có góc BAC=60 độ, tia phân giác góc BAC
bởi Thiên Mai
 11/04/2019
11/04/2019
Cho tam giác ABA vuông ở C, có góc BAC=60 độ,tia phân giác của góc BAC cắt BC ở E,kẻ EK vuông góc với AB(K thuộc AB).
a>Tính góc abc
b>Kẻ BD vuông góc vs AE(D thuộc AE).CM:AD=bc
d>so sánh EB,EC
#giải giúp e ạ
Theo dõi (0) 1 Trả lời -


Chứng minh AM=AN biết tam giác ABC có trên tia đối của tia AB lấy điểm D sao cho AD=AB
bởi Lê Tấn Thanh
 11/04/2019
11/04/2019
Cho tam giác ABC trên tia đối của tia AB lấy điểm D sao cho AD=AB,trên tia đối của tia AC lấy điểm E sao cho AE=AC.Gọi M là điểm nằm giữa B và Các,tia MA cắt DE ở N.Chứng mình rằng
A)góc ACB=góc AED
B) Góc DNM=góc CMN bù nhau
C)AM=AN
Help me <3
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có A=90° và AB=AC.Qua A vẽ đường thẳng d bất kì ko cắt cạnh BC.Từ B và Các kẻ BH vuông góc độ và CK vuông góc độ.Gọi d là trung điểm của đoạn thẳng BC.Chứng minh
a)tam giác ABH=ACK
B)BH+CK=HK
C)AD là tia phân giác của góc BAC
Theo dõi (0) 1 Trả lời -


Cho ΔABC có AB=AC, kẻ AM là tia phân giác của góc A(m∈BC)
Chứng minh ΔABM=ΔACM
Kẻ MH(H∈AB), kẻ MK vuông góc CA(K∈AC). Chứng minh MH=MK
AM vuông góc với BC
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác DAK=BAC biết tam giác ABC có AM là phân giác của góc A và AD=AB
bởi Anh Trần
 11/04/2019
11/04/2019
Cho \(\Delta\)ABC (AB<AC) có AM là phân giác của góc A. (M thuộc BC). Trên AC lấy D sao cho AD=AB.
a, C/m BM=MD
b, Gọi K là giao điểm của AB và DM .C/m \(\Delta\)DAK=\(\Delta\)BAC
c, C/m \(\Delta\)AKC cân
d,So sánh BM và CM
Theo dõi (0) 1 Trả lời -

 Cho ΔABC cân tại A. trên cạnh AB lấy điểm D và trên tia đối của tia CA lấy điểm E sao cho CE = BD. Gọi I là giao điểm của DE và BC. Chứng minh DI=IE.Theo dõi (0) 1 Trả lời
Cho ΔABC cân tại A. trên cạnh AB lấy điểm D và trên tia đối của tia CA lấy điểm E sao cho CE = BD. Gọi I là giao điểm của DE và BC. Chứng minh DI=IE.Theo dõi (0) 1 Trả lời -


Chứng minh O là trung điểm của BH biết tam giác ABC có góc A=70 đô, AH vuông BC
bởi hà trang
 11/04/2019
11/04/2019
Cho \(\Delta ABC\) có \(\widehat{A}=70\) độ. Kẻ \(AH\perp BC\) tại H . Trên đường vuông góc với BC tại B lấy điểm D (D và A không cùng nửa mặt phẳng bờ BC) sao cho AH = BD.
a, C/minh: \(\Delta AHB=\Delta DBH\)
b, C/minh: AB // HD
c, Gọi O là giao điểm của AD và BC. C/minh: O là trung điểm của BH
d, Tính \(\widehat{ACB}\) , biết \(\widehat{BDH}\) = 30 độ
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A có góc A =20 độ , vẽ tam giác DBC ( D nằm trong tam giác ABC ) . Tia phân giác của góc ABD cắt AC tại M . Chứng minh :
a, tia AD là tia phân giác của góc BAC
b, AM=BCTheo dõi (0) 1 Trả lời


