Giải bài 3.31 tr 178 SBT Toán 12
Tính diện tích hình phẳng giới hạn bởi các đường sau:
a) \(y = 2x - {x^2},x + y = 2\);
b) \(y = {x^3} - 12x,y = {x^2}\);
c) \(x + y = 1,x + y = - 1,x - y = 1,x - y = - 1\);
d) \(y = \frac{1}{{1 + {x^2}}},y = \frac{1}{2}\);
e) \(y = {x^3} - 1\) và tiếp tuyến với \(y = {x^3} - 1\) tại điểm (-1;-2).
Hướng dẫn giải chi tiết
a) Hoành độ giao điểm của hai đồ thị hàm số \(y = 2x - {x^2};y = - x + 2\) là:
\(2x - {x^2} = - x + 2 \Leftrightarrow {x^2} - 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 1\\
x = 2
\end{array} \right.\)
Vậy diện tích S của hình phẳng bằng
\(\begin{array}{l}
S = \int\limits_1^2 {\left[ {\left( {2x - {x^2}} \right) - \left( { - x + 2} \right)} \right]dx} \\
= \int\limits_1^2 {\left( {3x - {x^2} - 2} \right)dx} \\
= \left. {\left( {\frac{3}{2}{x^2} - \frac{{{x^3}}}{3} - 2x} \right)} \right|_1^2 = \frac{1}{6}\left( {dvdt} \right)
\end{array}\)
b) Hoành độ giao điểm của hai đồ thị hàm số \(y = {x^3} - 12x,y = {x^2}\) là:
\({x^3} - 12x = {x^2} \Leftrightarrow {x^3} - {x^2} - 12x = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 4\\
x = - 3
\end{array} \right.\)
Vậy diện tích S của hình phẳng bằng
\(\begin{array}{l}
S = \int\limits_{ - 3}^0 {\left( {{x^3} - 12x - {x^2}} \right)dx + \int\limits_4^0 {\left( {{x^2} - {x^3} + 12x} \right)dx} } \\
= \left. {\left( {\frac{{{x^4}}}{4} - 6{x^2} + \frac{{{x^3}}}{3}} \right)} \right|_{ - 3}^0 + \left. {\left( {\frac{{{x^3}}}{3} - \frac{{{x^4}}}{4} + 6{x^2}} \right)} \right|_0^4\\
= \frac{{99}}{4} + \frac{{160}}{3} = \frac{{937}}{{12}}\left( {dvdt} \right)
\end{array}\)
c) Ta có đồ thị của 4 hàm số đã cho:
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 39 trang 175 SGK Toán 12 NC
Bài tập 40 trang 175 SGK Toán 12 NC
Bài tập 3.32 trang 178 SBT Toán 12
Bài tập 3.33 trang 178 SBT Toán 12
Bài tập 3.34 trang 178 SBT Toán 12
Bài tập 3.35 trang 178 SBT Toán 12
Bài tập 3.36 trang 179 SBT Toán 12
Bài tập 3.37 trang 179 SBT Toán 12
Bài tập 3.38 trang 179 SBT Toán 12
Bài tập 3.39 trang 180 SBT Toán 12
Bài tập 3.40 trang 180 SBT Toán 12
-


Tính diện tích hình phẳng giới hạn bởi hai đường cong y=x^2-2x và y=x^2+4x-4
bởi luong van tuong
 16/03/2020
16/03/2020
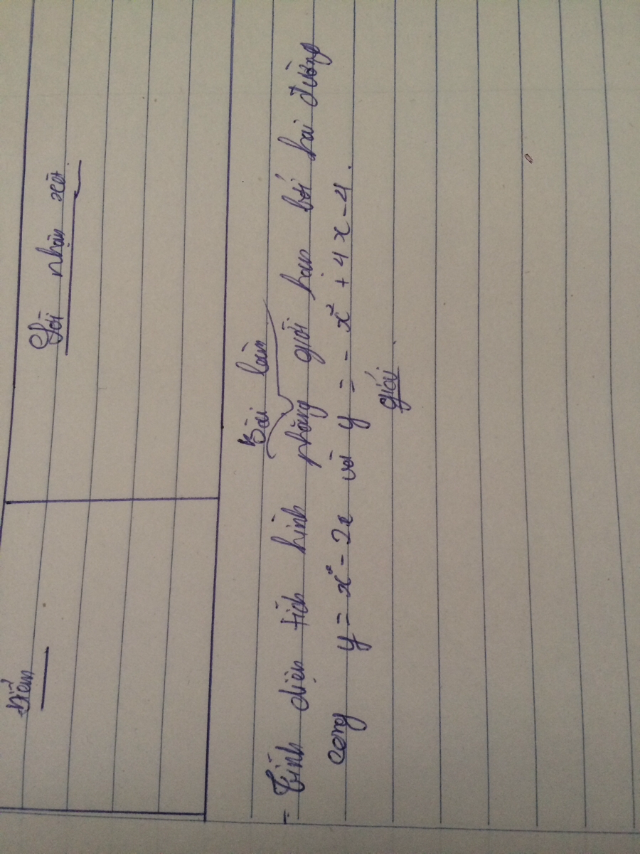 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Cho hình trụ có bán kính đáy bằng R. Tính thể tích vật thể tạo thành bởi đáy của hình trụ và mặt phẳng qua đường kính đáy, biết mặt phẳng tạo với đáy một góc 45°
bởi Thu Ngọc
 11/03/2020
Cho hình trụ có bán kính đáy bằng R. Tính thể tích vật thể tạo thành bởi đáy của hình trụ và mặt phẳng qua đường kính đáy, biết mặt phẳng tạo với đáy một góc 45°Theo dõi (0) 2 Trả lời
11/03/2020
Cho hình trụ có bán kính đáy bằng R. Tính thể tích vật thể tạo thành bởi đáy của hình trụ và mặt phẳng qua đường kính đáy, biết mặt phẳng tạo với đáy một góc 45°Theo dõi (0) 2 Trả lời -


Tính diện tích hình phẳng giới hạn bởi y = x^3 -4x trục Ox đường thẳng x = -1 ; x=1
bởi Phạm Duy Thanh
 09/03/2020
tính diện tích hình phẳng giới hạn bởi y = x^3 -4x trục Ox đường thẳng x = -1 ; x=1Theo dõi (0) 1 Trả lời
09/03/2020
tính diện tích hình phẳng giới hạn bởi y = x^3 -4x trục Ox đường thẳng x = -1 ; x=1Theo dõi (0) 1 Trả lời -


Tính diện tích hình phẳng giới hạn bởi (C) y = f(x)= x^2 với các tiếp tuyến của (C) xuất phát từ A(1/6;-10/3)
bởi Nay Y Tuyên
 04/03/2020
tính diện tích hình phẳng giới hạn bởi (c) y = f(x)= x^2 với các tiếp tuyến của (c) xuất phát từ A(1/6;-10/3)Theo dõi (0) 1 Trả lời
04/03/2020
tính diện tích hình phẳng giới hạn bởi (c) y = f(x)= x^2 với các tiếp tuyến của (c) xuất phát từ A(1/6;-10/3)Theo dõi (0) 1 Trả lời -
ADMICRO


Tìm diện tích hình phẳng giới hạn bởi đồ thị hàm số y=e^x trục Ox trục Oy và đường thẳng x=1
bởi Mai Vy
 26/02/2020
Tìm diện tích hình phẳng giới hạn bởi đồ thị hàm số y=e^x trục Ox trục Oy và đường thẳng x=1Theo dõi (0) 1 Trả lời
26/02/2020
Tìm diện tích hình phẳng giới hạn bởi đồ thị hàm số y=e^x trục Ox trục Oy và đường thẳng x=1Theo dõi (0) 1 Trả lời -


Tính diện tích của đường hầm hình parabol đi qua núi có chiều cao OI=9m, chiều rộng AB=10m
bởi Huynh Vy
 23/02/2020
Tính
23/02/2020
Tính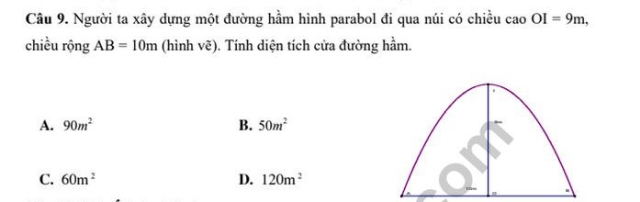 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời


