Bài tập 3.32 trang 178 SBT Toán 12
Tính thể tích vật thể:
a) Có đáy là một tam giác cho bởi: y = x , y = 0 , và x = 1. Mỗi thiết diện vuông góc với trục Ox là một hình vuông.
b) Có đáy là một hình tròn giới hạn bởi x2 + y2 = 1. Mỗi thiết diện vuông góc với trục Ox là một hình vuông.
Hướng dẫn giải chi tiết
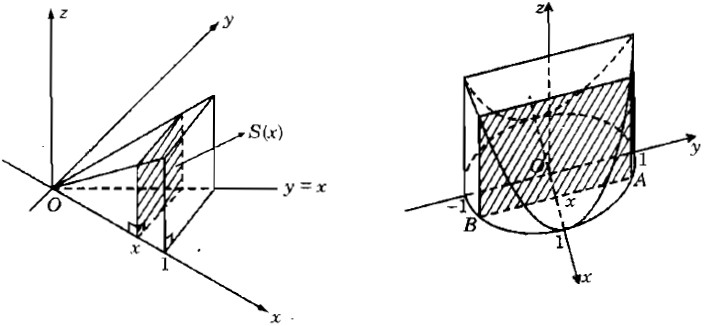
a) Với x ∈ [0;1] là hình vuông cạnh bằng x, S(x) = x2.
Vậy \(V = \int \limits_0^1 S(x)dx = \int \limits_0^1 {x^2}dx = \frac{1}{3}\)
b) Thiết diện tại x∈[−1;1] là hình vuông cạnh AB, trong đó A(x; y) với \(y = \sqrt {1 - {x^2}} \).
Khi đó, \(AB = 2\sqrt {1 - {x^2}} \).
Diện tích thiết diện là: \(S(x) = 4(1 - {x^2})\)
Vậy:
\(\begin{array}{l}
V = 4\int \limits_{ - 1}^1 (1 - {x^2})dx\\
= 8\int \limits_0^1 (1 - {x^2})dx = \frac{{16}}{3}
\end{array}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 40 trang 175 SGK Toán 12 NC
Bài tập 3.31 trang 178 SBT Toán 12
Bài tập 3.33 trang 178 SBT Toán 12
Bài tập 3.34 trang 178 SBT Toán 12
Bài tập 3.35 trang 178 SBT Toán 12
Bài tập 3.36 trang 179 SBT Toán 12
Bài tập 3.37 trang 179 SBT Toán 12
Bài tập 3.38 trang 179 SBT Toán 12
Bài tập 3.39 trang 180 SBT Toán 12
Bài tập 3.40 trang 180 SBT Toán 12
-

 câu 54
câu 54 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -

 Tính diện tích hình phằn giới hạn bởi 3 đường y=x^3-3x;y=1;y=xTheo dõi (0) 0 Trả lời
Tính diện tích hình phằn giới hạn bởi 3 đường y=x^3-3x;y=1;y=xTheo dõi (0) 0 Trả lời -

 Y=x^4-3x^2 m
Y=x^4-3x^2 m Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Cho mình xin cách làm ah
Cho mình xin cách làm ah Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Tính thể tích của khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường và quay xung quanh trục Ox
bởi Ánh Trần Ngọc
 29/01/2020
29/01/2020
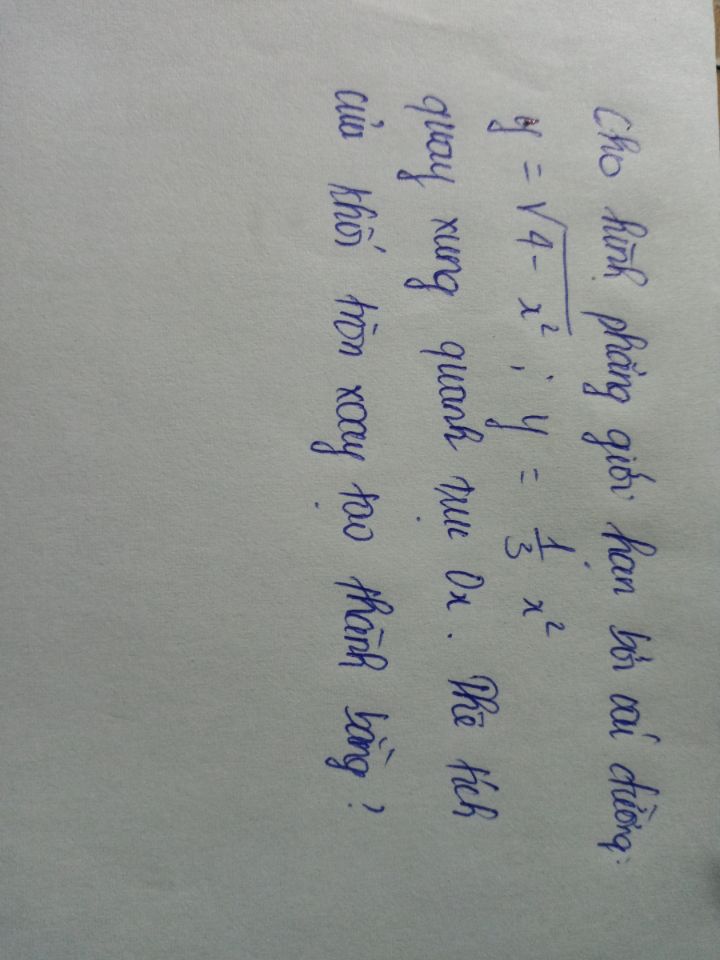 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Diện tích hình phẳng giới hạn bởi đồ thi hàm số y=|x^2-4x 3| và y=x 3 có kết quả dạng a/b, khi đó a 2b?
bởi Hoàng Thu Ngân
 17/01/2020
Giải thích hộ e bàu này vs ạ e cảm ơn
17/01/2020
Giải thích hộ e bàu này vs ạ e cảm ơn Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời


