HÆ°áŧng dášŦn GiášĢi bà i tášp ToÃĄn 11 CÃĄnh Diáŧu ChÆ°ÆĄng 1 Bà i 2 CÃĄc phÃĐp biášŋn Äáŧi lÆ°áŧĢng giÃĄc mÃīn ToÃĄn háŧc láŧp 11 giÚp cÃĄc em háŧc sinh nášŊm váŧŊng phÆ°ÆĄng phÃĄp giášĢi bà i tášp và Ãīn luyáŧn táŧt kiášŋn tháŧĐc.
-
Kháŧi Äáŧng trang 16 SGK ToÃĄn 11 CÃĄnh Diáŧu Tášp 1 - CD
áŧ láŧp dÆ°áŧi, ta ÄÃĢ là m quen váŧi máŧt sáŧ phÃĐp tÃnh trong tášp háŧĢp cÃĄc sáŧ tháŧąc, chášģng hᚥn: phÃĐp tÃnh luáŧđ tháŧŦa váŧi sáŧ mÅĐ táŧą nhiÊn và nháŧŊng cÃīng tháŧĐc Äáŧ tÃnh toÃĄn hay biášŋn Äáŧi nháŧŊng biáŧu tháŧĐc cháŧĐa cÃĄc luáŧđ tháŧŦa nhÆ° vášy. Viáŧc lášĨy cÃĄc giÃĄ tráŧ lÆ°áŧĢng giÃĄc cáŧ§a gÃģc lÆ°áŧĢng giÃĄc ÄÃĢ hÃŽnh thà nh nÊn nháŧŊng phÃĐp tÃnh máŧi trong tášp háŧĢp cÃĄc sáŧ tháŧąc, ÄÃģ là nháŧŊng phÃĐp tÃnh lÆ°áŧĢng giÃĄc.

CÃģ hay khÃīng nháŧŊng cÃīng tháŧĐc Äáŧ tÃnh toÃĄn hay biášŋn Äáŧi nháŧŊng biáŧu tháŧĐc cháŧĐa giÃĄ tráŧ lÆ°áŧĢng giÃĄc?
-
Hoᚥt Äáŧng 1 trang 16 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
Cho tam giÃĄc MNP cÃģ ÄÆ°áŧng cao PQ (HÃŽnh 17).
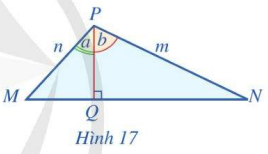
a) Viášŋt cÃīng tháŧĐc tÃnh PQ theo cᚥnh n và gÃģc a; cÃīng tháŧĐc tÃnh PQ theo cᚥnh m và gÃģc b
b) Viášŋt cÃīng tháŧĐc tÃnh diáŧn tÃch máŧi tam giÃĄc MPQ, NPQ, MNP theo cÃĄc cᚥnh m, n và cÃĄc cᚥnh m, n và cÃĄc gÃģc a, b, a + b
c) Sáŧ dáŧĨng kášŋt quášĢ: \[{S_{MPN}} = {S_{MPQ}} + {S_{NPQ}}\]
HÃĢy tÃŽm cÃīng tháŧĐc tÃnh sin(a+b) theo sina, cosa, sinb, cosb. TáŧŦ ÄÃģ rÚt ra Äášģng sin(a + b) = sina.cosb + cosa.sinb (â).
d) TÃnh sin(aâb) bášąng cÃĄch biášŋn Äáŧi sin(aâb) = sin[a + (âb)] và sáŧ dáŧĨng cÃīng tháŧĐc (*).
-
Luyáŧn tášp 1 trang 16 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
TÃnh \(\frac{\pi }{{12}}\).
-
Hoᚥt Äáŧng 2 trang 17 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
a) TÃnh \(\cos (a + b)\) bášąng cÃĄch biášŋn Äáŧi \(cos\left( {a + b} \right) = sin\left( {\frac{\pi }{2} - \left( {a + b} \right)} \right) = \sin \left( {\left( {\frac{\pi }{2} - a} \right) - b} \right)\) và sáŧ dáŧĨng cÃīng tháŧĐc cáŧng Äáŧi váŧi sin.
b) TÃnh \(\cos (a â b)\) bášąng cÃĄch biášŋn Äáŧi \(\cos (a â b)\) = \(\cos [a + (-b)]\) và sáŧ dáŧĨng cÃīng tháŧĐc \(\cos (a + b)\) cÃģ ÄÆ°áŧĢc áŧ cÃĒu a.
- VIDEOYOMEDIA
-
Luyáŧn tášp 2 trang 17 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
TÃnh \(cos{15^o}\).
-
Hoᚥt Äáŧng 3 trang 17 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
a) Sáŧ dáŧĨng cÃīng tháŧĐc cáŧng Äáŧi váŧi sin và cÃīsin, hÃĢy tÃnh \(\tan (a + b)\) theo tana và tanb khi cÃĄc biáŧu tháŧĐc Äáŧu cÃģ nghÄĐa.
b) Khi cÃĄc biáŧu tháŧĐc Äáŧu cÃģ nghÄĐa, hÃĢy tÃnh \(\tan (a - b)\) bášąng cÃĄch biášŋn Äáŧi
\(\tan (a - b) = \tan [a + ( - b)]\) và sáŧ dáŧĨng cÃīng tháŧĐc \(\tan (a + b)\) cÃģ ÄÆ°áŧĢc áŧ cÃĒu a.
-
Luyáŧn tášp 3 trang 17 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
TÃnh \(tan165^\circ \).
-
Hoᚥt Äáŧng 4 trang 18 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
TÃnh \(\sin 2a,\cos 2a,\tan 2a\) bášąng cÃĄch thay \(b = a\) trong cÃīng tháŧĐc cáŧng.
-
Luyáŧn tášp 4 trang 18 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
Cho \(\tan \frac{a}{2} = - 2\). TÃnh tana?
-
Luyáŧn tášp 5 trang 18 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
TÃnh: \(\sin \frac{\pi }{8};\cos \frac{\pi }{8}\).
-
Hoᚥt Äáŧng 5 trang 18 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
Sáŧ dáŧĨng cÃīng tháŧĐc cáŧng, rÚt gáŧn máŧi biáŧu tháŧĐc sau:
\(\cos (a + b) + \cos (a - b);\cos (a + b) - \cos (a - b);\sin (a + b) + \sin (a - b)\)
-
Luyáŧn tášp 6 trang 19 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
Cho \(\cos a = \frac{2}{3}\). TÃnh \(B = \cos \frac{{3a}}{2}\cos \frac{a}{2}\).
-
Hoᚥt Äáŧng 6 trang 6 SGK ToÃĄn 19 CÃĄnh Diáŧu tášp 1 - CD
Sáŧ dáŧĨng cÃīng tháŧĐc biášŋn Äáŧi tÃch thà nh táŧng và Äáš·t a + b = u; a â b = v ráŧi biášŋn Äáŧi cÃĄc biáŧu tháŧĐc sau thà nh tÃch: \(\cos u + \cos v;\sin u + \sin v;\sin u - \sin v\)
-
Luyáŧn tášp 7 trang 19 SGK ToÃĄn 11 CÃĄnh Diáŧu tášp 1 - CD
TÃnh: \(D = \frac{{\sin \frac{{7\pi }}{9} + \sin \frac{\pi }{9}}}{{{\rm{cos}}\frac{{7\pi }}{9} - \cos \frac{\pi }{9}}}\).
-
GiášĢi BÃ i 1 trang 20 SGK ToÃĄn 11 CÃĄnh Diáŧu Tášp 1 - CD
Cho \(\cos \alpha = \frac{3}{5}\) váŧi \(0 < \alpha < \frac{\pi }{2}\). TÃnh \(\sin \left( {a + \frac{\pi }{6}} \right)\), \(\cos \left( {a - \frac{\pi }{3}} \right)\), \(\tan \left( {a + \frac{\pi }{4}} \right)\).
-
GiášĢi BÃ i 2 trang 20 SGK ToÃĄn 11 CÃĄnh Diáŧu Tášp 1 - CD
TÃnh:
a) \(A = \sin (a - {17^o})\cos (a + {13^o}) - \sin (a + {13^o})\cos (a - {17^o})\).
b) \(B = \cos \left( {b + \frac{\pi }{3}} \right)\cos \left( {\frac{\pi }{6} - b} \right) - \sin \left( {b + \frac{\pi }{3}} \right)\sin \left( {\frac{\pi }{6} - b} \right)\).
-
GiášĢi BÃ i 3 trang 20 SGK ToÃĄn 11 CÃĄnh Diáŧu Tášp 1 - CD
Cho tan(a + b) = 3, tan(a â b) = 2. TÃnh: tan2a, tan2b.
-
GiášĢi BÃ i 4 trang 20 SGK ToÃĄn 11 CÃĄnh Diáŧu Tášp 1 - CD
Cho \(\sin a = \frac{2}{{\sqrt 5 }}\). TÃnh cos2a, cos4a.
-
GiášĢi BÃ i 5 trang 20 SGK ToÃĄn 11 CÃĄnh Diáŧu Tášp 1 - CD
Cho sina + cosa = 1. TÃnh: sin2a.
-
GiášĢi BÃ i 6 trang 20 SGK ToÃĄn 11 CÃĄnh Diáŧu Tášp 1 - CD
Cho \(\cos 2a = \frac{1}{3}\) váŧi \(\frac{\pi }{2} < a < \pi \). TÃnh: sina, cosa, tana.
-
GiášĢi BÃ i 7 trang 21 SGK ToÃĄn 11 CÃĄnh Diáŧu Tášp 1 - CD
Cho cos2x = . TÃnh: A = coscos; B = sinsin.
-
GiášĢi BÃ i 8 trang 21 SGK ToÃĄn 11 CÃĄnh Diáŧu Tášp 1
RÚt gáŧn biáŧu tháŧĐc: A = .
-
GiášĢi BÃ i 9 trang 21 SGK ToÃĄn 11 CÃĄnh Diáŧu Tášp 1 - CD
Máŧt sáŧĢi cÃĄp R ÄÆ°áŧĢc gášŊn và o máŧt cáŧt thášģng ÄáŧĐng áŧ váŧ trà cÃĄch máš·t ÄášĨt 14 m. Máŧt sáŧĢi cÃĄp S khÃĄc cÅĐng ÄÆ°áŧĢc gášŊn và o cáŧt ÄÃģ áŧ váŧ trà cÃĄch máš·t ÄášĨt 12 m. Biášŋt rášąng hai sáŧĢi cÃĄp trÊn cÃđng ÄÆ°áŧĢc gášŊn váŧi máš·t ÄášĨt tᚥi máŧt váŧ trà cÃĄch chÃĒn cáŧt 15 m (HÃŽnh 18).
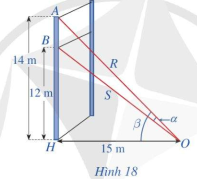
a) TÃnh tanÎą, áŧ ÄÃģ Îą là gÃģc giáŧŊa hai sáŧĢi cÃĄp trÊn.
b) TÃŽm gÃģc Îą (là m trÃēn kášŋt quášĢ Äášŋn hà ng ÄÆĄn váŧ theo ÄÆĄn váŧ Äáŧ).
RÚt gáŧn biáŧu tháŧĐc: A = .
-
GiášĢi BÃ i 10 trang 21 SGK ToÃĄn 11 CÃĄnh Diáŧu Tášp 1 - CD
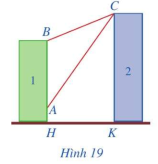
CÃģ hai chung cÆ° cao tᚧng I và II xÃĒy cᚥnh nhau váŧi khoášĢng cÃĄch giáŧŊa chÚng là HK = 20 m. Äáŧ ÄášĢm bášĢo an ninh, trÊn nÃģc chung cÆ° II ngÆ°áŧi ta lášŊp camera áŧ váŧ trà C. Gáŧi A, B lᚧn lÆ°áŧĢt là váŧ trà thášĨp nhášĨt, cao nhášĨt trÊn chung cÆ° I mà camera cÃģ tháŧ quan sÃĄt ÄÆ°áŧĢc (HÃŽnh 19). HÃĢy tÃnh sáŧ Äo gÃģc ACB (phᚥm vi camera cÃģ tháŧ quan sÃĄt ÄÆ°áŧĢc áŧ chung cÆ° I). Biášŋt rášąng chiáŧu cao cáŧ§a chung cÆ° II là CK = 32 m, AH = 6 m, BH = 24 m (là m trÃēn kášŋt quášĢ Äášŋn hà ng phᚧn mÆ°áŧi theo ÄÆĄn váŧ Äáŧ).
-
Bà i tášp 15 trang 14 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Cho hai gÃģc \(a\) và \(b\) váŧi \(\tan a = \frac{1}{7}\) và \(\tan b = \frac{3}{4}\). Khi ÄÃģ \(\tan \left( {a + b} \right)\) bášąng:
A. \(1\)
B. \( - \frac{{17}}{{31}}\)
C. \(\frac{{17}}{{31}}\)
D.\( - 1\)
-
Bà i tášp 16 trang 14 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Nášŋu \(\sin \alpha = \frac{1}{{\sqrt 3 }}\) váŧi \(0 < \alpha < \frac{\pi }{2}\) thÃŽ giÃĄ tráŧ cáŧ§a \(\cos \left( {\alpha + \frac{\pi }{3}} \right)\) bášąng:
A. \(\frac{{\sqrt 6 }}{6} - \frac{1}{2}\)
B. \(\sqrt 6 - 3\)
C. \(\frac{{\sqrt 6 }}{6} - 3\)
D. \(\sqrt 6 - \frac{1}{2}\)
-
Bà i tášp 17 trang 14 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Nášŋu \(\sin \alpha = \frac{2}{3}\) thÃŽ giÃĄ tráŧ cáŧ§a biáŧu tháŧĐc \(P = \left( {1 - 3\cos 2\alpha } \right)\left( {2 + 3\cos 2\alpha } \right)\) bášąng:
A. \(\frac{{11}}{9}\)
B. \(\frac{{12}}{9}\)
C. \(\frac{{13}}{9}\)
D. \(\frac{{14}}{9}\)
-
Bà i tášp 18 trang 15 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Cháŧn Äášģng tháŧĐc ÄÚng trong cÃĄc Äášģng tháŧĐc sau:
A. \({\sin ^4}x + {\cos ^4}x = \frac{{3 - \cos 4x}}{4}\)
B. \({\sin ^4}x + {\cos ^4}x = \frac{{3 + \cos 4x}}{4}\)
C. \({\sin ^4}x + {\cos ^4}x = \frac{{3 + \cos 4x}}{2}\)
D. \({\sin ^4}x + {\cos ^4}x = \frac{{3 - \cos 4x}}{2}\)
-
Bà i tášp 19 trang 15 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
RÚt gáŧn biáŧu tháŧĐc \(\cos \left( {{{120}^o} - x} \right) + \cos \left( {{{120}^o} + x} \right) - \cos x\) ta ÄÆ°áŧĢc kášŋt quášĢ là :
A. \( - 2\cos x\)
B. \( - \cos x\)
C. \(0\)
D. \(\sin x - \cos x\)
-
Bà i tášp 20 trang 15 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Nášŋu \(\cos a = \frac{3}{4}\) thÃŽ giÃĄ tráŧ cáŧ§a \(\cos \frac{a}{2}\cos \frac{a}{2}\) bášąng:
A. \(\frac{{23}}{{16}}\)
B. \(\frac{7}{8}\)
C. \(\frac{7}{{16}}\)
D. \(\frac{{23}}{8}\)
-
Bà i tášp 21 trang 15 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Nášŋu \(\cos a = \frac{{\sqrt 5 }}{3}\) thÃŽ giÃĄ tráŧ cáŧ§a biáŧu tháŧĐc \(A = 4\sin \left( {a + \frac{\pi }{3}} \right)\sin \left( {a - \frac{\pi }{3}} \right)\) bášąng:
A. \( - \frac{{11}}{9}\)
B. \(\frac{{11}}{9}\)
C. \( - \frac{1}{9}\)
D. \(\frac{1}{9}\)
-
Bà i tášp 22 trang 15 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Nášŋu \(\cos a = \frac{1}{3}\), \(\sin b = \frac{{ - 2}}{3}\) thÃŽ giÃĄ tráŧ \(\cos \left( {a + b} \right)\cos \left( {a - b} \right)\) bášąng:
A. \( - \frac{2}{3}\)
B. \(\frac{1}{3}\)
C. \(\frac{2}{3}\)
D. \( - \frac{1}{3}\)
-
Bà i tášp 23 trang 15 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
GiÃĄ tráŧ cáŧ§a biáŧu tháŧĐc \(P = \frac{{\sin \frac{\pi }{9} + \sin \frac{{5\pi }}{9}}}{{\cos \frac{\pi }{9} + \cos \frac{{5\pi }}{9}}}\) bášąng:
A. \(\frac{1}{{\sqrt 3 }}\)
B. \( - \frac{1}{{\sqrt 3 }}\)
C. \(\sqrt 3 \)
D. \( - \sqrt 3 \)
-
Bà i tášp 24 trang 15 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
RÚt gáŧn biáŧu tháŧĐc \(A = \frac{{\sin x + \sin 2x + \sin 3x}}{{\cos x + \cos 2x + \cos 3x}}\) ta ÄÆ°áŧĢc kášŋt quášĢ là :
A. \(\tan x\)
B. \(\tan 3x\)
C. \(\tan 2x\)
D. \(\tan x + \tan 2x + \tan 3x\)
-
Bà i tášp 25 trang 15 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Cho \(\sin a = \frac{2}{3}\) váŧi \(\frac{\pi }{2} < a < \pi \). TÃnh:
a) \(\cos a\), \(\tan a\)
b) \(\sin \left( {a + \frac{\pi }{4}} \right)\), \(\cos \left( {a - \frac{{5\pi }}{6}} \right)\), \(\tan \left( {a + \frac{{2\pi }}{3}} \right)\)
c) \(\sin 2a\), \(\cos 2a\)
-
Bà i tášp 26 trang 15 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Cho \(\cos a = 0,2\) váŧi \(\pi < a < 2\pi \). TÃnh \(\sin \frac{a}{2}\), \(\cos \frac{a}{2}\), \(\tan \frac{a}{2}\)?
-
Bà i tášp 27 trang 15 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Cho \(\tan \frac{a}{2} = \frac{1}{{\sqrt 2 }}\). TÃnh \(\sin a\), \(\cos a\), \(\tan a\)?
-
Bà i tášp 28 trang 16 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Cho \(\cos \left( {a + 2b} \right) = 2\cos a\). CháŧĐng minh rášąng \(\tan \left( {a + b} \right)\tan b = \frac{{ - 1}}{3}\)?
-
Bà i tášp 29 trang 16 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
Cho tam giÃĄc \(ABC\), cháŧĐng minh rášąng:
a) \(\tan A + \tan B + \tan C = \tan A{\rm{ }}{\rm{. }}\tan B{\rm{ }}{\rm{. }}\tan C\) (váŧi Äiáŧu kiáŧn tam giÃĄc \(ABC\) khÃīng vuÃīng);
b) \(\tan \frac{A}{2}{\rm{ }}{\rm{. }}\tan \frac{B}{2} + \tan \frac{B}{2}{\rm{ }}{\rm{. }}\tan \frac{C}{2} + \tan \frac{C}{2}{\rm{ }}{\rm{. }}\tan \frac{A}{2} = 1\).
-
Bà i tášp 30 trang 16 SBT ToaĖn 11 TÃĒĖĢp 1 CaĖnh diÊĖu - CD
TrÊn máŧt mášĢnh ÄášĨt hÃŽnh vuÃīng \(ABCD\), bÃĄc An Äáš·t máŧt chiášŋc ÄÃĻn pin tᚥi váŧ trà \(A\) chiášŋu chÃđm sÃĄng phÃĒn kÃŽ sang phÃa gÃģc \(C\). BÃĄc An nhášn thášĨy gÃģc chiášŋu sÃĄng cáŧ§a ÄÃĻn pin giáŧi hᚥn báŧi hai tia \(AM\) và \(AN\), áŧ ÄÃģ cÃĄc Äiáŧm \(M\), \(N\) lᚧn lÆ°áŧĢt thuáŧc cÃĄc cᚥnh \(BC\), \(CD\) sao cho \(BM = \frac{1}{2}BC\), \(DN = \frac{1}{3}DC\) (xem hÃŽnh váš―).
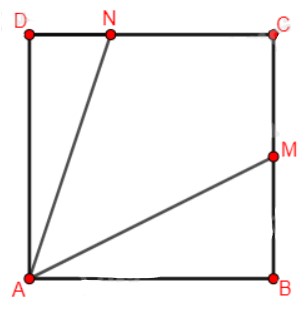
a) TÃnh \(\tan \left( {\widehat {BAM} + \widehat {DAN}} \right)\)?
b) GÃģc chiášŋu sÃĄng cáŧ§a ÄÃĻn pin bášąng bao nhiÊu Äáŧ?


