Giải bài 6.57 tr 193 SBT Toán 10
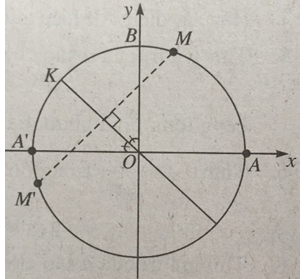
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = 80ο trong đó A(1; 0). Gọi M' là điểm đối xứng với M qua đường phân giác của góc phần tư thứ II. Số đo của cung lượng giác AM' là:
A. 170ο B. - 200ο
C. 190ο D. 280ο
Hướng dẫn giải chi tiết
Sđ MK = sđ KM’ = 55o
⇒ sđ AM’ = sđ AM + sđ MK + sđ KM’ = 190o.
Đáp án: C
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 6.55 trang 193 SBT Toán 10
Bài tập 6.56 trang 193 SBT Toán 10
Bài tập 6.59 trang 193 SBT Toán 10
Bài tập 6.58 trang 193 SBT Toán 10
Bài tập 55 trang 217 SGK Toán 10 NC
Bài tập 56 trang 218 SGK Toán 10 NC
Bài tập 57 trang 218 SGK Toán 10 NC
Bài tập 58 trang 218 SGK Toán 10 NC
Bài tập 59 trang 218 SGK Toán 10 NC
Bài tập 60 trang 219 SGK Toán 10 NC
Bài tập 61 trang 219 SGK Toán 10 NC
Bài tập 62 trang 219 SGK Toán 10 NC
Bài tập 63 trang 219 SGK Toán 10 NC
Bài tập 64 trang 219 SGK Toán 10 NC
Bài tập 65 trang 219 SGK Toán 10 NC
Bài tập 66 trang 219 SGK Toán 10 NC
Bài tập 67 trang 220 SGK Toán 10 NC
-
Chứng minh đồng nhất thức: \(\displaystyle \tan x - \tan y = {{\sin (x - y)} \over {\cos x.cosy}}\).
bởi Nguyễn Thị Thanh
19/02/2021
Theo dõi (0) 1 Trả lời -
Chứng minh đồng nhất thức: \(\displaystyle {{2\cos 2x - \sin 4x} \over {2\cos 2x + \sin 4x}} = {\tan ^2}({\pi \over 4} - x)\).
bởi Phan Thị Trinh
19/02/2021
Theo dõi (0) 1 Trả lời -
Chứng minh đồng nhất thức: \(\displaystyle {{{\mathop{\rm \sin x}\nolimits} + \sin{x \over 2}} \over {1 + \cos x + \cos {x \over 2}}} = \tan {x \over 2}\).
bởi A La
19/02/2021
Theo dõi (0) 1 Trả lời -
Chứng minh đồng nhất thức: \(\displaystyle {{1 - \cos x + \cos 2x} \over {\sin 2x - {\mathop{\rm s}\nolimits} {\rm{in x}}}} = \cot x\).
bởi Tram Anh
19/02/2021
Theo dõi (0) 1 Trả lời -
ADMICRO
Tính: \(\cos {12^0} - \cos {48^0} = \sin {18^0}\).
bởi Phan Thị Trinh
19/02/2021
Theo dõi (0) 1 Trả lời -
Theo dõi (0) 1 Trả lời -
Tính: \(\tan {267^0} + \tan {93^0} = 0\).
bởi Trinh Hung
20/02/2021
Theo dõi (0) 1 Trả lời -
Theo dõi (0) 1 Trả lời -
Theo dõi (0) 1 Trả lời -
Tính: \(\displaystyle \sin {{25\pi } \over 3} - \tan {{10\pi } \over 3}\)
bởi Lê Minh Hải
20/02/2021
Theo dõi (0) 1 Trả lời -
Tính: \(\displaystyle \sin {{23\pi } \over 4}\)
bởi Lê Viết Khánh
20/02/2021
Theo dõi (0) 1 Trả lời -
Tính: \(\displaystyle \cos {{22\pi } \over 3}\)
bởi Ban Mai
20/02/2021
Theo dõi (0) 1 Trả lời -
Rút gọn biểu thức: \(\displaystyle {{\sin 5\alpha - \sin 3\alpha } \over {2\cos 4\alpha }}\)
bởi can tu
19/02/2021
Theo dõi (0) 1 Trả lời
