Phᚧn hÆ°áŧng dášŦn giášĢi bà i tášp ToÃĄn 8 ChÃĒn tráŧi sÃĄng tᚥo ChÆ°ÆĄng 3 Bà i 4 HÃŽnh bÃŽnh hà nh â HÃŽnh thoi sáš― giÚp cÃĄc em nášŊm ÄÆ°áŧĢc phÆ°ÆĄng phÃĄp và rÃĻn luyáŧn kÄĐ nÄng, giášĢi bà i tášp táŧŦ SGK ToÃĄn 8 ChÃĒn tráŧi sÃĄng tᚥo.
-
Kháŧi Äáŧng trang 73 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Quan sÃĄt hÃŽnh cháŧĨp cÃĄc mÃĄi nhà áŧ pháŧ cáŧ Háŧi An, em thášĨy cÃĄc cᚥnh Äáŧi cáŧ§a táŧĐ giÃĄc ABCD cÃģ gÃŽ Äáš·c biáŧt?

-
KhÃĄm phÃĄ 1 trang 73 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
HÃŽnh 1a là hÃŽnh ášĢnh cáŧ§a máŧt thÆ°áŧc váš― truyáŧn dÃđng Äáŧ phÃģng to hay thu nháŧ máŧt hÃŽnh váš― cÃģ sášĩn. DÃđng thÆ°áŧc Äo gÃģc Äáŧ Äo sáŧ Äo cáŧ§a cÃĄc cáš·p gÃģc và , và cáŧ§a táŧĐ giÃĄc ABCD (HÃŽnh 1b) ráŧi rÚt ra nhášn xÃĐt váŧ máŧi quan háŧ giáŧŊa cÃĄc cáš·p cᚥnh AB và CD; AD và BC?

-
KhÃĄm phÃĄ 2 trang 74 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
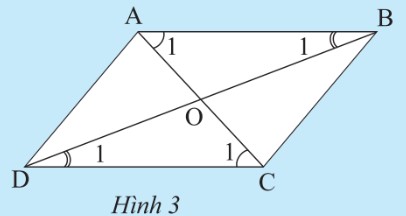
Cho táŧĐ giÃĄc ABCD cÃģ cÃĄc cᚥnh Äáŧi song song. Gáŧi O là giao Äiáŧm cáŧ§a hai ÄÆ°áŧng chÃĐo. HÃĢy cháŧĐng táŧ:
â Tam giÃĄc ABC bášąng tam giÃĄc CDA.
â Tam giÃĄc OAB bášąng tam giÃĄc OCD.
-
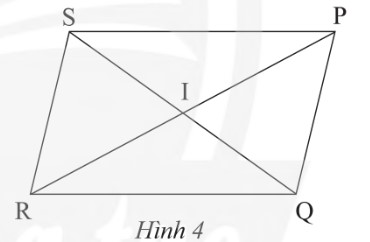
Tháŧąc hà nh 1 trang 74 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Cho hÃŽnh bÃŽnh hà nh PQRS váŧi I là giao Äiáŧm cáŧ§a hai ÄÆ°áŧng chÃĐo (HÃŽnh 4). HÃĢy cháŧ ra cÃĄc Äoᚥn thášģng bášąng nhau và cÃĄc gÃģc bášąng nhau cÃģ trong hÃŽnh?
- VIDEOYOMEDIA
-
Vášn dáŧĨng 1 trang 74 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
MášŊt lÆ°áŧi cáŧ§a máŧt lÆ°áŧi bÃģng chuyáŧn cÃģ dᚥng hÃŽnh táŧĐ giÃĄc cÃģ cÃĄc cᚥnh Äáŧi song song. Cho biášŋt Äáŧ dà i hai cᚥnh cáŧ§a táŧĐ giÃĄc nà y là 4 cm và 5 cm. TÃŽm Äáŧ dà i hai cᚥnh cÃēn lᚥi?

-
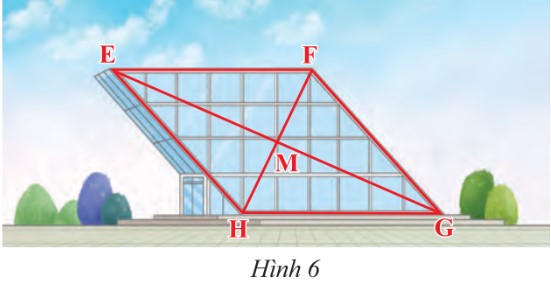
Vášn dáŧĨng 2 trang 74 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Máš·t trÆ°áŧc cáŧ§a máŧt cÃīng trÃŽnh xÃĒy dáŧąng ÄÆ°áŧĢc là m bášąng kÃnh cÃģ dᚥng hÃŽnh bÃŽnh hà nh EFGH váŧi M là giao Äiáŧm cáŧ§a hai ÄÆ°áŧng chÃĐo (HÃŽnh 6). Cho biášŋt EF = 40 m, EM = 36 m, HM = 16 m. TÃnh Äáŧ dà i cᚥnh HG và Äáŧ dà i hai ÄÆ°áŧng chÃĐo?
-
KhÃĄm phÃĄ 3 trang 75 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
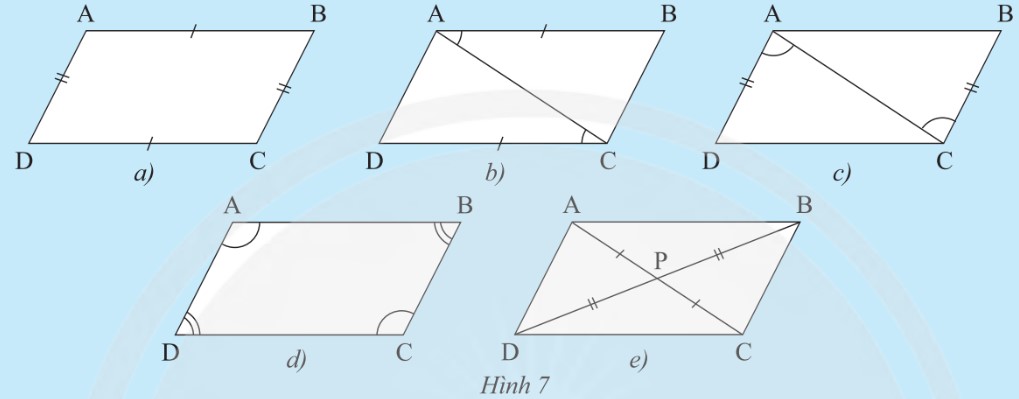
Cho táŧĐ giÃĄc ABCD cÃģ P là giao Äiáŧm cáŧ§a hai ÄÆ°áŧng chÃĐo. GiášĢi thÃch tᚥi sao AB // CD và AD // BC trong máŧi trÆ°áŧng háŧĢp sau:
TrÆ°áŧng háŧĢp 1: \(AB = CD\) và \(AD = BC\) (HÃŽnh 7a).
TrÆ°áŧng háŧĢp 2: \(AB // CD\) và \(AB = CD\) (HÃŽnh 7b).
TrÆ°áŧng háŧĢp 3: \(AD // BC\) và \(AD = BC\) (HÃŽnh 7c).
TrÆ°áŧng háŧĢp 4: (HÃŽnh 7d).
TrÆ°áŧng háŧĢp 5: \(PA = PC, PB = PD\) (HÃŽnh 7e).
-
Tháŧąc hà nh 2 trang 76 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
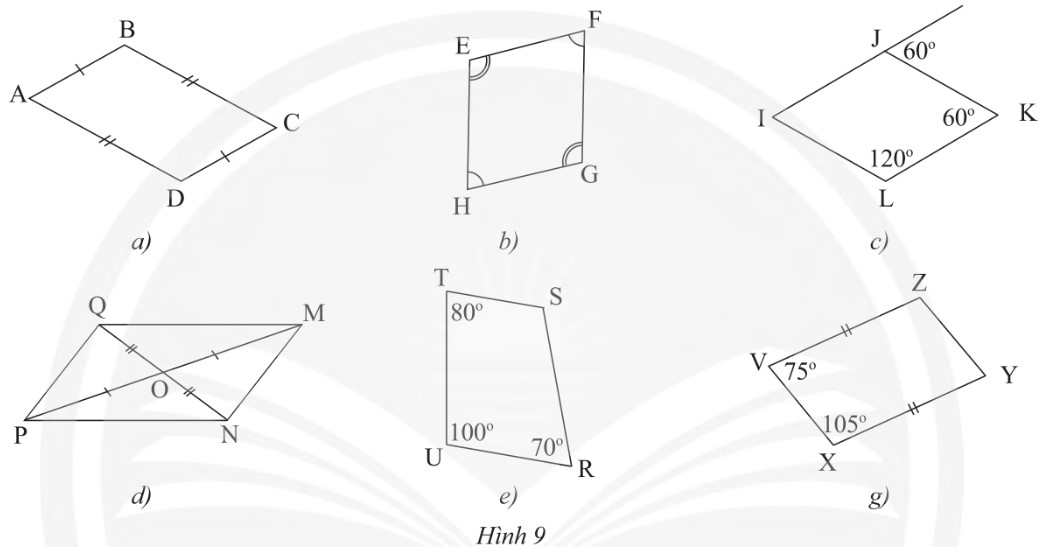
Trong cÃĄc táŧĐ giÃĄc áŧ HÃŽnh 9, táŧĐ giÃĄc nà o khÃīng là hÃŽnh bÃŽnh hà nh?
-
Vášn dáŧĨng 3 trang 76 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
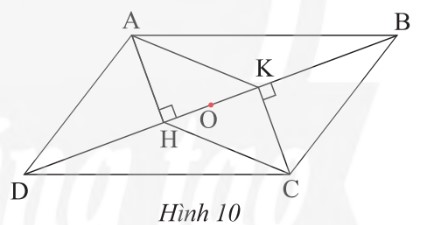
Quan sÃĄt HÃŽnh 10, cho biášŋt ABCD và AKCH Äáŧu là hÃŽnh bÃŽnh hà nh. CháŧĐng minh ba Äoᚥn thášģng AC, BD và HK cÃģ cÃđng trung Äiáŧm O?
-
KhÃĄm phÃĄ 4 trang 76 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
HÃŽnh 11a là hÃŽnh cháŧĨp tášĨm lÆ°áŧi thÃĐp ÄÆ°áŧĢc Äan thà nh nhiáŧu mášŊt. HÃŽnh 11b là hÃŽnh váš― phÃģng to cáŧ§a máŧt mášŊt lÆ°áŧi. Äo Äáŧ dà i cÃĄc cᚥnh cáŧ§a táŧĐ giÃĄc ABCD và rÚt ra nhášn xÃĐt?

-
KhÃĄm phÃĄ 5 trang 77 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
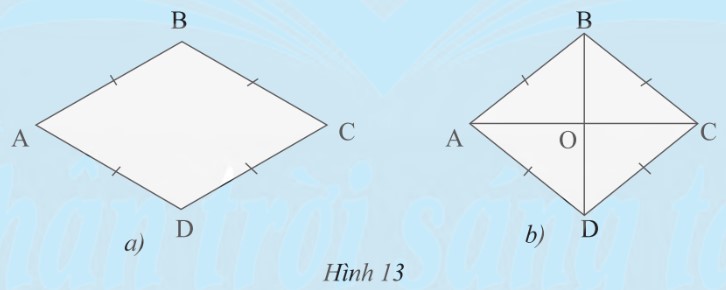
a) HÃŽnh thoi cÃģ là hÃŽnh bÃŽnh hà nh khÃīng?
b) Cho hÃŽnh thoi ABCD cÃģ O là giao Äiáŧm cáŧ§a hai ÄÆ°áŧng chÃĐo (HÃŽnh 13b). CÃĄc tam giÃĄc OAB, OCB, OCD, OAD cÃģ bášąng nhau khÃīng?
-
Tháŧąc hà nh 3 trang 78 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Cho hÃŽnh thoi MNPQ cÃģ I là giao Äiáŧm cáŧ§a hai ÄÆ°áŧng chÃĐo.
a) TÃnh MP khi biášŋt MN = 10 dm, IN = 6 dm.
b) TÃnh khi biášŋt .
-
Vášn dáŧĨng 4 trang 78 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
TÃnh Äáŧ dà i cᚥnh cáŧ§a cÃĄc khuy ÃĄo hÃŽnh thoi cÃģ Äáŧ dà i hai ÄÆ°áŧng chÃĐo lᚧn lÆ°áŧĢt là 3,2 cm và 2,4 cm?
-
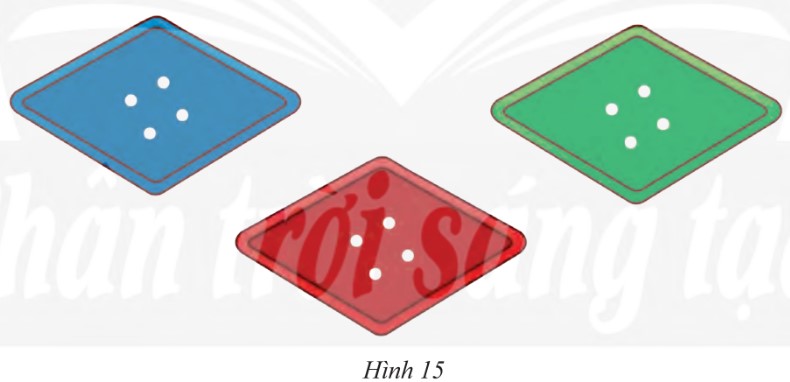
KhÃĄm phÃĄ 6 trang 78 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Cho ABCD là máŧt hÃŽnh bÃŽnh hà nh. GiášĢi thÃch tᚥi sao táŧĐ giÃĄc ABCD cÃģ báŧn cᚥnh bášąng nhau trong máŧi trÆ°áŧng háŧĢp sau:
TrÆ°áŧng háŧĢp 1: AB = AD.
TrÆ°áŧng háŧĢp 2: AC vuÃīng gÃģc váŧi BD.
TrÆ°áŧng háŧĢp 3: AC là ÄÆ°áŧng phÃĒn giÃĄc gÃģc BAD.
TrÆ°áŧng háŧĢp 4: BD là ÄÆ°áŧng phÃĒn giÃĄc gÃģc ABC.
-
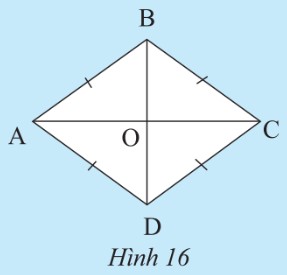
Vášn dáŧĨng 5 trang 79 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Máŧt hoa vÄn trang trà ÄÆ°áŧĢc ghÃĐp báŧi ba hÃŽnh táŧĐ giÃĄc cÃģ Äáŧ dà i máŧi cᚥnh Äáŧu bášąng 2 cm (HÃŽnh 18). Gáŧi tÊn cÃĄc táŧĐ giÃĄc nà y và tÃnh chu vi cáŧ§a hoa vÄn?

-
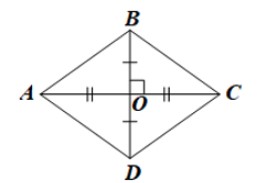
Vášn dáŧĨng 6 trang 79 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Máŧt táŧĐ giÃĄc cÃģ chu vi là 52 cm và máŧt ÄÆ°áŧng chÃĐo là 24 cm. TÃŽm Äáŧ dà i cáŧ§a máŧi cᚥnh và ÄÆ°áŧng chÃĐo cÃēn lᚥi nášŋu biášŋt hai ÄÆ°áŧng chÃĐo vuÃīng gÃģc tᚥi trung Äiáŧm cáŧ§a máŧi ÄÆ°áŧng?
-
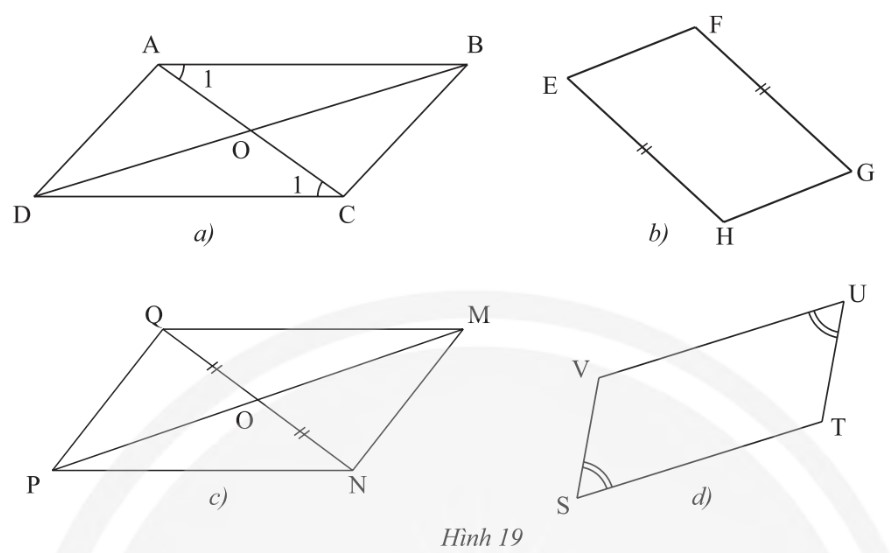
BÃ i 1 trang 80 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Cᚧn thÊm máŧt Äiáŧu kiáŧn gÃŽ Äáŧ máŧi táŧĐ giÃĄc trong HÃŽnh 19 tráŧ thà nh hÃŽnh bÃŽnh hà nh?
-
BÃ i 2 trang 80 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
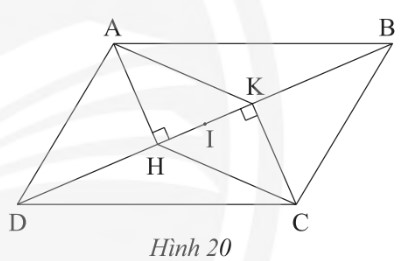
Cho hÃŽnh bÃŽnh hà nh ABCD, kášŧ AH vuÃīng gÃģc váŧi BD tᚥi H và CK vuÃīng gÃģc váŧi BD tᚥi K (HÃŽnh 20).
a) CháŧĐng minh táŧĐ giÃĄc AHCK là hÃŽnh bÃŽnh hà nh.
b) Gáŧi I là trung Äiáŧm cáŧ§a HK. CháŧĐng minh IB = ID.
-
BÃ i 3 trang 80 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Cho hÃŽnh bÃŽnh hà nh \(ABCD\). Gáŧi E là trung Äiáŧm cáŧ§a AD, F là trung Äiáŧm cáŧ§a BC.
a) CháŧĐng minh rášąng táŧĐ giÃĄc \(EBFD\) là hÃŽnh bÃŽnh hà nh.
b) Gáŧi O là giao Äiáŧm cáŧ§a hai ÄÆ°áŧng chÃĐo cáŧ§a hÃŽnh bÃŽnh hà nh \(ABCD\). CháŧĐng minh rášąng ba Äiáŧm E, O, F thášģng hà ng.
-
BÃ i 4 trang 80 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Cho hÃŽnh bÃŽnh hà nh \(ABCD\) (AB > BC). Tia phÃĒn giÃĄc cáŧ§a gÃģc D cášŊt AB tᚥi E, tia phÃĒn giÃĄc cáŧ§a gÃģc B cášŊt CD tᚥi F.
a) CháŧĐng minh \(DE // BF\)?
b) TáŧĐ giÃĄc \(DEBF\) là hÃŽnh gÃŽ?
-
BÃ i 5 trang 80 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Cho hÃŽnh bÃŽnh hà nh \(ABCD\). Gáŧi I và K lᚧn lÆ°áŧĢt là trung Äiáŧm cáŧ§a cÃĄc cᚥnh AB và CD; E và F lᚧn lÆ°áŧĢt là giao Äiáŧm cáŧ§a AK và CI váŧi BD.
a) CháŧĐng minh táŧĐ giÃĄc \(AEFI\) là hÃŽnh thang.
b) CháŧĐng minh \(DE = EF = FB\).
-
BÃ i 6 trang 81 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
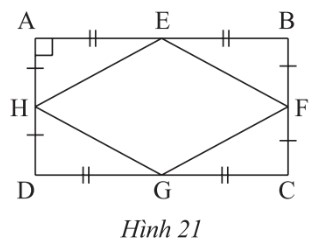
Quan sÃĄt HÃŽnh 21. CháŧĐng minh rášąng táŧĐ giÃĄc EFGH là hÃŽnh thoi?
-
BÃ i 7 trang 81 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
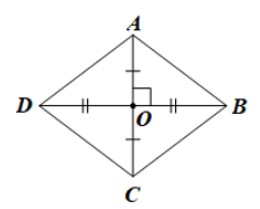
Cho hÃŽnh thoi ABCD, hai ÄÆ°áŧng chÃĐo AC và BD cášŊt nhau tᚥi O. Biášŋt AC = 6 cm, BD = 8 cm. TÃnh Äáŧ dà i cᚥnh cáŧ§a hÃŽnh thoi ABCD?
-
BÃ i 8 trang 81 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
Cho tam giÃĄc \(ABC\) cÃĒn tᚥi A, gáŧi M là trung Äiáŧm cáŧ§a BC. LášĨy Äiáŧm D Äáŧi xáŧĐng váŧi Äiáŧm A qua BC.
a) CháŧĐng minh táŧĐ giÃĄc \(ABDC\) là hÃŽnh thoi?
b) Gáŧi E, F lᚧn lÆ°áŧĢt là trung Äiáŧm cáŧ§a AB và AC, lášĨy Äiáŧm O sao cho E là trung Äiáŧm cáŧ§a OM. CháŧĐng minh hai tam giÃĄc \(AOB\) và \(MBO\) vuÃīng và bášąng nhau?
c) CháŧĐng minh táŧĐ giÃĄc \(AEMF\) là hÃŽnh thoi?
-
BÃ i 9 trang 81 SGK ToaĖn 8 ChÃĒn trÆĄĖi saĖng taĖĢo TÃĒĖĢp 1 - KNTT
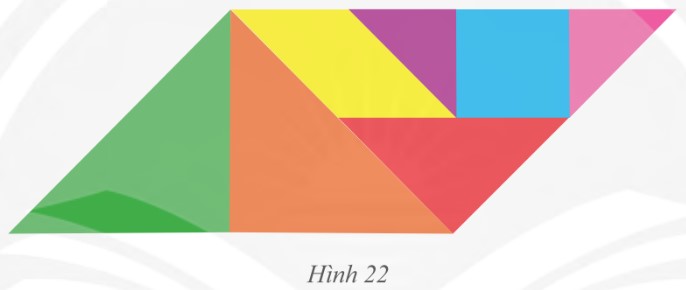
TÃŽm cÃĄc hÃŽnh bÃŽnh hà nh và hÃŽnh thang cÃģ trong HÃŽnh 22?