Bài 5 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT

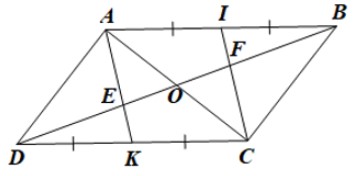
a) Do \(ABCD\) là hình bình hành nên \(AB = CD\) và \(AB // CD\).

Vì I là trung điểm của AB nên $AI=IB=\frac{1}{2}AB$.

Vì K là trung điểm của CD nên $CK=DK=\frac{1}{2}CD$.

Do đó \(AI = CK\).

Tứ giác \(AICK\) có \(AI // CK\) (do \(AB // CD\)) và \(AI = CK\) nên là hình bình hành (dấu hiệu nhận biết).

Suy ra \(AK // CI\) hay \(AE // IF\).

Tứ giác \(AEFI\) có \(AE // IF\) nên là hình thang.

b) Gọi O là giao điểm của hai đường chéo hình bình hành \(ABCD\).

Do đó O là trung điểm của AC và BD.

Xét \(\Delta{ABC}\) có BO, CI là hai đường trung tuyến của tam giác và BO, CI cắt nhau tại F nên F là trọng tâm của \( \Delta{ABC}\).

Suy ra $BF=\frac{2}{3}BO$ và $FO=\frac{1}{3}BO$.

Chứng minh tương tự đối với \( \Delta{ACD}\) ta cũng có E là trọng tâm của \( \Delta{ACD}\).

Suy ra $DE=\frac{2}{3}DO$ và $EO=\frac{1}{3}DO$.

Lại có O là trung điểm BD nên \(BO = DO\).

Do đó $BF=DE=\frac{2}{3}BO$ và $FO=EO=\frac{1}{3}BO$

Mặt khác $EF=EO+FO=\frac{1}{3}BO+\frac{1}{3}BO=\frac{2}{3}BO$.

Suy ra $DE=EF=FB=\frac{2}{3}BO$.

Vậy \(DE = EF = FB\).

-- Mod Toán 8 HỌC247