Khám phá 6 trang 78 SGK Toán 8 Chân trời sáng tạo Tập 1
Cho ABCD là một hình bình hành. Giải thích tại sao tứ giác ABCD có bốn cạnh bằng nhau trong mỗi trường hợp sau:
Trường hợp 1: AB = AD.
Trường hợp 2: AC vuông góc với BD.
Trường hợp 3: AC là đường phân giác góc BAD.
Trường hợp 4: BD là đường phân giác góc ABC.
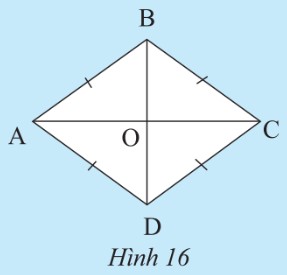
Hướng dẫn giải chi tiết Khám phá 6
- Trường hợp 1: AB = AD.
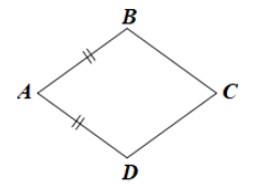
Vì ABCD là hình bình hành nên AD = BC và AB = CD.
Lại có AB = AD (giả thiết)
Do đó AB = AD = BC = CD.
- Trường hợp 2: AC vuông góc với BD.
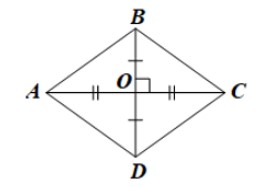
Vì ABCD là hình bình hành nên AD = BC, AB = CD và hai đường chéo AC, BD cắt nhau tại trung điểm O của mỗi đường.
Xét DOAB và DOCB có:
; OB là cạnh chung; OA = OC
Do đó DOAB = DOCB (hai cạnh góc vuông)
Suy ra AB = CB (hai cạnh tương ứng).
Mà AD = BC và AB = CD nên AB = CD = CB = DA.
- Trường hợp 3: AC là đường phân giác góc BAD.
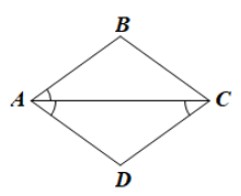
Vì ABCD là hình bình hành nên AB // CD
Do đó (so le trong).
Mà (do AC là tia phân giác của góc BAD)
Suy ra .
Tam giác ACD có nên là tam giác cân tại D
Suy ra DA = DC.
Lại có AB = CD và AD = BC (chứng minh trên).
Do đó AB = BC = CD = DA.
- Trường hợp 4: BD là đường phân giác góc ABC.
Chứng minh tương tự như trường hợp 3 ta cũng có AB = BC = CD = DA.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Thực hành 3 trang 78 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Vận dụng 4 trang 78 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Vận dụng 5 trang 79 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Vận dụng 6 trang 79 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 1 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 2 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 3 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 4 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 5 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 6 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 7 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 8 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 9 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


