Vận dụng 6 trang 79 SGK Toán 8 Chân trời sáng tạo Tập 1
Một tứ giác có chu vi là 52 cm và một đường chéo là 24 cm. Tìm độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường?
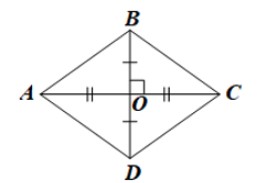
Hướng dẫn giải chi tiết Vận dụng 6
Tứ giác ABCD có hai đường chéo vuông góc tại trung điểm của mỗi đường nên là hình thoi.
Độ dài cạnh của hình thoi ABCD là: \(52 : 4 = 13\) (cm).
Giả sử đường chéo \(AC = 24 cm\) và O là giao điểm hai đường chéo.
Ta có O là trung điểm của AC nên \(OA = \frac{1}{2} AC = 12 cm\).
Áp dụng định lí Pythagore vào DOAB vuông tại O, ta có:
AB2 = OA2 + OB2
Suy ra (cm).
Do O là trung điểm của BD nên \(BD = 2OB = 2.5 = 10\) (cm).
Vậy hình thoi có độ dài cạnh là 13 cm và độ dài đường chéo còn lại là 10 cm.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Khám phá 6 trang 78 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Vận dụng 5 trang 79 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 1 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 2 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 3 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 4 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 5 trang 80 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 6 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 7 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 8 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 9 trang 81 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


