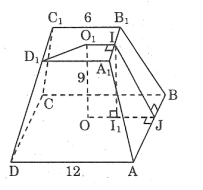
Bài tập 71 trang 153 SBT Toán 8 Tập 2

Tìm GTNN của biểu thức:

A= x² - 2xy + 6y² - 12x + 2y + 45

Cho x+y =1 và xy=-1 .Tính x³ + y³

b) Cho a - b = 1 và ab= 6. Tính a³ - b³

c) Cho a+b=1.Tính a³ + b³ +3ab

HELP ME!!?!!!

Tìm x, y nguyên thõa mãn:

2xy=5.(x+y)+8

Câu 1: Thực hiện phép tính

a. \(x^2.\left(5x^3-x-\dfrac{1}{2}\right)\)

b. \(\left(x-2\right)\left(6x^2-5x+1\right)\)

Câu 2: Phân tích ĐT thành NT

a. x²+5x+6

Câu 3. Cho biểu thức: \(B=\left(\dfrac{1}{x-2}-\dfrac{1}{x}\right):\dfrac{1}{x-2}\)

a. Tìm ĐKXĐ

b. Rút gọn B

c. Tính giá trị của Biểu thức B khi \(x=\dfrac{3}{5}\)

Câu 4: Cho đa thức: \(f\left(x\right)=x^{2016}+x^{2015}+x^3+x\)

Tìm đa thức dư trong phép chia: \(f\left(x\right):\left(x^2-1\right)\)

Giúp em vsssss

Mí bác ơi~~

Ai giải giùm em với a~~~

Bài 1:Phân tích đa thức thành nhân tử

d,\(x^2+2xy+y^2-9\)

Bài 2:Làm tính chia

\(\left(x^4-x^3-3x^2+x+2\right):\left(x^2-1\right)\)

Bài 3:Chứng minh rằng giá trị của biểu thức sau luôn dương với mọi x:

\(x^2-2x+5\)

Tìm GTLN

C= -x\(^2\)-2.x+3

D=-4x\(^2\)-6x-7

Tìm GTLN của biểu thức: C= 2x+5-x²

Tìm x biết

3x(x-1) + 1 - x = 0

25 - x ^2 + 2 x - 1 = 0

( x - 3) tất cả bình phương - ( x+3)(x-1) = 7

Phân tích thành nhân tử : A = ( x² + y²)³ + ( z² - x²)³ - ( y² + z²)³

Tìm a , b sao cho : x³ + ax² + 2x + b chia hết cho x² + x + 1

Giải các phương trình sau:

a). ( 4x – 8)(25 + 5x) = 0

b). |x – 1 | = 3x + 2

9^8.2^8-(18^4-1)(18^4+1)

(a+b)^3+(a-b)^3-2a^3

Rút gọn

3(2² +1)(2⁴ +1)(2⁸ +1)(2¹⁶ +1)

Rút gọn

(6x+1)² + ( 6x-1)² - 2(1+6x)(6x-1)

(27x^3 - 8 ) : ( 6x + 9x ^2 + 4 )

Phân tích đa thức thành nhân tử

bài 1 Phân tích đa thức thành nhân tử:( pp thêm bớt hoặc tách)

1) x^4+64

2)x^3+2x^2+5x+4

3) x^3-x^2+10

cần sự giúp đỡ

Giải các phương trình sau:

a) 2x – 3 = 5

b) (3x – 2)(4x + 5) = 0

bài 2 tìm x

1) x^3+2x^2+2x+4=0

2) x^3+4x^2-2x-8=0

3)x^3+3x-4=0

4)x^3+x-30=0

help

Tìm GTNN của biểu thức: x^2+4y^2+4x-4y-3

rút gọn

B = (3x + 2y )(3x - 2y)- (3x - 1)^2 + (2y + 1)^2

cmr: các góc của 1 tứ giác ko thể đều là góc nhọn, ko thể đều là góc tù.

1) Tìm x:

a. \(x^3-\dfrac{1}{4}x=0\) b. \(\left(2x-1\right)^2-\left(x+3\right)^2=0\)

c. \(2x^2-x-6=0\)

2) Cho biểu thức \(B=\left(\dfrac{x}{x^2-36}-\dfrac{x-6}{x^2+6x}\right):\dfrac{2x-6}{x^2+6x}\)

a.Rút gọn B.

b. Tính giá trị của B tại x = 2

Tìm tất cả các cặp số nguyên (x,y) thoa man :

10x²+50y²+42xy+14x-6y+57 <0

Phân tích đa thức thành nhân tử:

a)x²+4

b)(x+2)(x+3)(x+4)(x+5)-25

c)x²+7x+6

d)x⁴+2008x²+2007x+2008

1) Phân tích các đa thức sau thành nhân tử:

a. \(^{3x^2-3y^2}\) c. \(x^2-3x+2\)

b. \(x^2-xy+7x-7y\) d. \(x^3+2x^2+xy^2-16x\)

2) Thực hiện các phép tính sau:

a. \(\dfrac{2x+6}{3x^2-x}:\dfrac{x^2+3x}{1-3x}\) b. \(\dfrac{x^2+4x-3}{x^3+1}-\dfrac{x-1}{x^2-x+1}+\dfrac{2}{x+1}\)

Phân tích các đa thức sau thành nhân tử:

\(i,27x^3-27x^2+18x-4\)

tìm x;y nguyên dương sao cho

9xy+3x+3y=51

Phân tích đa thức thành nhân tử

Giải phương trình: \(\left(x-1\right)\left(x+2\right)\left(x-6\right)\left(x-3\right)=34\)

Lẹ lên nhé mk đg cần gấp đó !!!

Phân tích đa thức thành nhân tử

x⁵ - 5x³ + 4x

1,Tính

a,(3+x)(x^2-9)-(x-3)(x^2+3x+9)

b,(x+6)^2-2x(x+6)+(x-6)(x+6)

mk cần gấp giúp mk vs

tìm x biết

A) (4x-1)²-(3x+2) (3x-2)=(7x-1) (x+2) + (2x+1)²-(4x¹+7)

B) (2x+3)²-(5x-4) (5x+4)=(x+5)²-(3x-1) (7x+2)-(x²-x+1)

C) (1-3x)²-(x-2) (9x+1)=(3x-4) (3x+4)-9(x+3)²

D) (3x+4) (3x-4) - (2x+5)²=(x-5)²+(2x+1)²-(x²-2x)+(x-1)² cần gắp

Tính tổng:

B = 1/1.2.3 + 1/2.3.4 + 1/3.4.5 +...+ 1/n(n+1)(n+2)

10 Phân tích các đa thức sau thành nhân tử:

a) 5xy(x-y)-2x+2y ; b) 6x-2y-x(y-3x)

c) x^2+4x-xy-4y ; d) 3xy+2z-6y-xz

11 Tìm x, biết: a) 4-9x^2=0 ; b) x^2+x+1/4=0 ; c) 2x(x-3)+(x-3)=0

d) 3x(x-4)-x+4=0 ; e) x^3-1/9x=0 ; f) (3x-y)^2-(x-y)^2=0

Giải phương trình
\(2x^4-7x^3+10x^2-7x+2=0\)

Phân tích các đa thức sau thành nhân tử:

\(e,x^2+y^2-x^2y^2+xy-x-y\)

\(f,x^4+2x^3-4x-4\)

Tìm giá trị của biểu thức

A) A=x3-15x2+75x-124 tại x=35

Phân tích đa thức sau thành nhân tử:

\(c,2x^2+x-3\)

\(d,6x^2-x-15\)

Phân tích đa thức sau thành nhân tử:

\(a,x^2-y^2-2y-1\)

\(b,x^2\left(1-x^2\right)-4+4x^2\)

rút gọn

a,(3x+1)²+2.(3x+1).(x-2)+(x-2)²

b,(4x+5)²-2.(4x+5).(4-5x)+(5x-4)²

Phân tích đa thức thành nhân tử bằng pp tách số:

a/ \(x^2-x-2\)

b/ \(x^2+x-2\)

hhepj hep hép mi

B=a^3-b^3-3ab biết a-b = 1

Rút gọn biểu thức :
A= (3⁸+1).(3⁴+1).(3²+1)(3+1)

B= 12.(5²+1).(5⁴+1).(5⁸+1)...(5³²+1)

tìm x biết :

x.(-3 + 2x ) -2x ( x-4 ) = 15

So sánh A=26^2-24^2 và B=27^2-25^2

Tính A = x³ - 3xy - y³ biết x - y = 1

giá trị số tự nhiên n thõa mãn : 1+2+2^2+2^3+...+2^32=2^n-1

câu 1: phân tích đa thức sau thành nhân tử:

a/ \(x^2-y^2+5x-5y\)

b/ \(x^2+4x+4\)

c/\(\left(x-3\right).\left(x+3\right)-\left(x-3\right)^2\)

câu 2: làm tính chia:

\(\left(x^4-2x^3+4x^2-8x\right).\left(x^2+4\right)\)

câu 3: chứng minh rằng: \(x^2-2x+2\)>0 với mọi x

Tìm x biết:

(x-2)³- (x-3)(x²+3x+9)+6(x+1)²=15

tim gtln x^2 + 5y^2 -4x +2xy -8y +2022

Phân tích đa thức thành nhân tử ( phối hợp các phương pháp )

x² - ( 2a + b ) xy + 2aby²

Các bạn giải gấp cho mình nha . Mình đag cần gấp /

Giải bpt: x^2 - 4 > 0

phân tích các đa thức sau thành nhân tử:

a,5x(x-11)-10y(x-11)

b,-x\(^2\)y\(^2\)z-6x\(^3\)y-8x\(^4\)z\(^2\)-9x\(^5\)y\(^5\)z\(^5\)

c,x\(^2\)-x+1+7x(x\(^2\)-x+1)

Cho hình chóp tứ giác đều có độ dài cạnh của tứ giác đáy bằng 4cm và độ dài đường cao bằng 6cm.Tính thể tích hình chóp đều

Cho phương trình (ẩn \(x\)):

                                \(4x^2-25+k^2+4kx=0\)

a) Giải phương trình với \(k=0\)

b) Giải phương trình vói \(k=-3\)

c) Tìm các giá trị của \(k\) sao cho phương trình nhận \(x=-2\) làm nghiệm