Bài tập 72 trang 153 SBT Toán 8 Tập 2
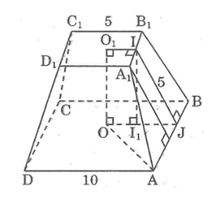
Cho hình chóp cụt tứ giác đều ABCD.A1B1C1D1 có các cạnh đáy 5cm và 10cm, đường cao mặt bên bằng 5cm. Hãy tính:
a) Diện tích xung quanh của hình chóp cụt.
b) Tính cạnh bên và đường cao hình chóp cụt.
Hướng dẫn giải chi tiết
Diện rích một mặt bên là hình thang bằng:
S =\(\frac{1}{2}\) (5 +10).5=37,5 (cm2)
Diện tích xung quanh của hình chóp
cụt đều là: Sxq =4.3,75 = 150 (cm2)
Kẻ A1H ⊥ AB, ta có:
A1I = 2,5cm; AJ = 5cm
Suy ra: AH = 2,5cm
Áp dụng định lí Pi-ta-go vào tam giác vuông A1HA, ta có:
A1A2 = A1H2 + AH2 = 52 + 2,52 = 31,25
Suy ra: A1A = \(\sqrt {31,25} \) ≈ 5,59 (cm)
Ta có: O1I = 2,5; OJ = 5cm.
Kẻ II1 ⊥ OJ, suy ra I1J = 2,5.
Áp dụng định kí Pi-ta-go vào tam giác vuông II1J, ta có:
IJ2 = II12 + I1J2
Suy ra: II12 = IJ2 – I1J2 = 52 – 2,52 = 18,75
Suy ra: II1 = \(\sqrt {18,75} \) ≈ 4,33 (cm)
Vậy O1O = II1 = 4,33 (cm)
-- Mod Toán 8 HỌC247
-


Tính diện tích toàn phần của hình chóp tứ giác đều biết cạnh đáy a=5cm, cạnh bên b=5cm
bởi Nguyễn Thị Thanh
 31/05/2019
31/05/2019
BT 48:tính diện tích toàn phần của:
a. hình chóp tứ giác đều, biết cạnh đáy a=5cm, cạnh bên b=5cm, \(\sqrt{18,75}\approx4,33\)
b. hình chóp lục giác đều, biết cạnh đáy a=6cm, cạnh bên b=10cm, \(\sqrt{3}\approx1,73;\sqrt{91}\approx9,54\)
Theo dõi (0) 1 Trả lời -


Bài 18 trang 7 SBT Toán 8 tập 2
bởi Nguyễn Minh Minh
 25/02/2019
Bài 18 (Sách bài tập - tập 2 - trang 7)
25/02/2019
Bài 18 (Sách bài tập - tập 2 - trang 7)Cho phương trình :
\(\left(m^2-4\right)x+2=m\)
Giải phương trình trong mỗi trường hợp sau :
a) \(m=2\)
b) \(m=-2\)
c) \(m=-2,2\)
Theo dõi (0) 1 Trả lời -


Bài 72 trang 154 sách bài tập toán 8 tập 2
bởi Ban Mai
 11/10/2018
11/10/2018
Bài 72 (Sách bài tập - tập 2 - trang 154)
Cho hình chóp cụt tứ giác đều \(ABCD.A_1B_1C_1D_1\) có các cạnh đáy 5cm và 10cm, đường cao của mặt bên bằng 5cm. Hãy tính :
a) Diện tích xung quanh của hình cụt
b) Tính cạnh bên và chiều cao của hình chóp cụt
Theo dõi (0) 1 Trả lời -


Bài 71 trang 154 sách bài tập toán 8 tập 2
bởi Nguyễn Thanh Hà
 11/10/2018
11/10/2018
Bài 71 (Sách bài tập - tập 2 - trang 154)
Tính diện tích toàn phần của hình chóp cụt đều cho theo các kích thước trên hình 154.
Theo dõi (0) 1 Trả lời -
ADMICRO


Bài 70 trang 154 sách bài tập toán 8 tập 2
bởi Dương Quá
 11/10/2018
11/10/2018
Bài 70 (Sách bài tập - tập 2 - trang 154)
Tính thể tích và diện tích toàn phần các hình chóp đều dưới đây (theo các kích thước cho trên hình vẽ 153)
Theo dõi (0) 1 Trả lời -


Bài 69 trang 152 sách bài tập toán 8 tập 2
bởi minh vương
 11/10/2018
11/10/2018
Bài 69 (Sách bài tập - tập 2 - trang 152)
Tính diện tích toàn phần của các hình chóp đều sau đây :
a) Hình cho theo các kích thước trên hình 152
b) Hình chóp tứ giác đều, cạnh đáy 6cm, chiều cao hình chóp 5cm
c) Hình chóp tứ giác đều, cạnh đáy 20cm, chiều cao hình chóp 7cm
d) Hình chóp tứ giác đều, cạnh đáy 1m, chiều cao hình chóp 50cm
Theo dõi (0) 1 Trả lời -


Bài 68 trang 152 sách bài tập toán 8 tập 2
bởi Phạm Phú Lộc Nữ
 29/09/2018
Bài 68 (Sách bài tập - tập 2 - trang 152)
29/09/2018
Bài 68 (Sách bài tập - tập 2 - trang 152)Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao hình chóp là 4cm. Thể tích của hình chóp là :
(A) \(30cm^3\) (B) \(24cm^3\)
(C) \(22cm^3\) (D) \(18cm^3\)
(E) \(15cm^3\)
Theo dõi (0) 1 Trả lời -


Bài 67 trang 152 sách bài tập toán 8 tập 2
bởi Lê Nhật Minh
 29/09/2018
Bài 67 (Sách bài tập - tập 2 - trang 152)
29/09/2018
Bài 67 (Sách bài tập - tập 2 - trang 152)Tính thể tích hình chóp tứ giác đều O.ABCD ? (Các kích thước cho trên hình 151)
Theo dõi (0) 1 Trả lời -


Bài 66 trang 152 sách bài tập toán 8 tập 2
bởi hành thư
 29/09/2018
Bài 66 (Sách bài tập - tập 2 - trang 152)
29/09/2018
Bài 66 (Sách bài tập - tập 2 - trang 152)Thể tích hình chóp đều cho theo các kích thước ở hình 150 là :
(A) \(54\sqrt{3}cm^3\) (B) \(540\sqrt{3}cm^3\)
(C) \(180\sqrt{3}cm^3\) (D) \(108\sqrt{3}cm^3\)
Hãy chọn kết quả đúng ?
Theo dõi (0) 1 Trả lời -


Bài 65 trang 151 sách bài tập toán 8 tập 2
bởi Nguyễn Thị Lưu
 11/10/2018
11/10/2018
Bài 65 (Sách bài tập - tập 2 - trang 151)
Xét các hình sau :
1) Kim tự tháp Kê - ốp (Thế kỉ 25 trước Công nguyên) là một hình chóp tứ giác đều, cạnh đáy bằng 233m , chiều cao hình chóp 146,5m
a) Độ dài cạnh bên là bao nhiêu ?
b) Tính diện tích xung quanh của hình chóp
c) Tính thể tích hình chóp
2) Kim tự tháp Lu - vrơ (Louvre) (Xây dựng vào năm 1988)
Người ta làm mô hình một kim tự tháp ở cổng vào của bảo thàng Lu - vrơ (Pháp). Mô hình có hạng hình chóp đều chiều cao 21m, độ dài cạnh đáy là 34m
a) Cạnh bên của hình chóp là bao nhiêu ?
b) Tính thể tích hình chóp ?
c) Tính tổng diện tích các tấm kính để phù lên hình chóp này (\(S_{xq}\))
Theo dõi (0) 1 Trả lời -


Bài 64 trang 151 sách bài tập toán 8 tập 2
bởi khanh nguyen
 11/10/2018
11/10/2018
Bài 64 (Sách bài tập - tập 2 - trang 151)
Hình 149 là chiếc lều ở một trại hè với các kích thước cho trên hình. ABC là một tam giác vuông cân
a) Tính thể tích của lều
b) Số vải bạt cần phải có để dựng lều đó là bao nhiêu ?
(Không tính các mép gấp, đương viền,.....)
Theo dõi (0) 1 Trả lời -


Bài 62 trang 150 sách bài tập toán 8 tập 2
bởi Dương Quá
 29/09/2018
Bài 62 (Sách bài tập - tập 2 - trang 150)
29/09/2018
Bài 62 (Sách bài tập - tập 2 - trang 150)Một hình chóp tứ giác đều là một lăng trụ đứng tứ giác đều như hình 147 dưới đây (cạnh đáy và chiều cao bằng nhau) :
Nếu thể tích lăng trụ là V thì thể tích hình chóp là :
(A) \(V\) (B) \(\dfrac{V}{2}\)
(C) \(\dfrac{V}{3}\) (D) \(\dfrac{V}{4}\)
Hãy chọn kết quả đúng ?
Theo dõi (0) 1 Trả lời -


Một hình chóp tứ giác đều có cạnh đáy 8cm và trung đoạn của hình chóp là 5cm. Tính thể tích hình chóp.
Theo dõi (0) 1 Trả lời -


Giải phương trình (x+1)(x+4)(x-2)^2 = 10x^2
bởi thanh duy
 25/02/2019
25/02/2019
\(\text{Giải phương trình : (x+1)(x+4)(x-2)}^2=10x^2\)
Theo dõi (0) 1 Trả lời -


Giải phương trình nghiệm nguyên x^2+y^2=3-xy
bởi Nguyễn Quang Minh Tú
 25/02/2019
25/02/2019
Giải phương trình nghiệm nguyên: \(x^2+y^2=3-xy\)
Theo dõi (0) 1 Trả lời -


Giải phương trình sau |2x|=x-6
bởi con cai
 25/02/2019
25/02/2019
Giải phương trình sau: |2x|=x-6
Theo dõi (0) 1 Trả lời -


1. Giải phương trình nghiệm nguyên x2y2 - x2 - 8y2 = 2xy
HELP...... MAI MÌNH PHẢI NỘP RỒI
MÌNH CẢM ƠN
Theo dõi (0) 1 Trả lời -


Giải phương trình chứa ẩn ở mẫu ( Nâng cao )
4/-25x^2+20x-3 = 3/5x-1 - 2/5x-3
Theo dõi (0) 1 Trả lời -


Giải phương trình |x - 2 | + 3| = 5
bởi Việt Long
 25/02/2019
25/02/2019
Giai phương trình :
e ) || x - 2 | + 3| = 5
Theo dõi (0) 1 Trả lời -


Giải phương trình |2x - 5|= 2 - x
bởi Mai Thuy
 25/02/2019
25/02/2019
Giai phương trình :
c.| 2x - 5 |= 2 - x
Theo dõi (0) 1 Trả lời -


Giải phương trình ∣5/4−x/2∣=x−1
bởi Nguyễn Vân
 25/02/2019
25/02/2019
Giai phương trình
b ) \(\left|\frac{5}{4}-\frac{x}{2}\right|=x-1\)
Theo dõi (0) 1 Trả lời -


Giải phương trình |x−2|−3x=5
bởi Ha Ku
 25/02/2019
25/02/2019
Giai phương trình :
a ) \(\left|x-2\right|-3x=5\)
Theo dõi (0) 1 Trả lời -


a) Phân tích : a) \(x^2-3x+2\) ; \(2x^2+3x+1\)
b) Giải phương trình : \(\left(2^x-8\right)^3+\left(4^x+13\right)^3=\left(4^x+2^x+5\right)^3\)
Theo dõi (0) 1 Trả lời -


Giải phương trình (x+3)(4−3x)+(x2+6x+9)=0
bởi Quế Anh
 25/02/2019
25/02/2019
Giai phương trình sau :
\(\left(x+3\right)\left(4-3x\right)+\left(x^2+6x+9\right)=0\)
Theo dõi (0) 1 Trả lời -


Giải phương trình (2−x)(2x−1)+(4x^2−4x+1)=0
bởi Nguyễn Vân
 25/02/2019
25/02/2019
Giai phuong trinh sau :
c ) \(\left(2-x\right)\left(2x-1\right)+\left(4x^2-4x+1\right)=0\)
Theo dõi (0) 1 Trả lời -


Giải phương trình x−3/4−5=1−2(x+3)/5
bởi Phan Thiện Hải
 25/02/2019
25/02/2019
Giai phương trình sau :
\(\frac{x-3}{4}-5=\frac{1-2\left(x+3\right)}{5}\)
Mình còn hai baì nữa các bạn giúp nha
Theo dõi (0) 1 Trả lời -


Giải phương trình ∣x^2−2x∣=x
bởi hi hi
 25/02/2019
25/02/2019
Giai phương trình :
\(\left|x^2-2x\right|=x\)
Theo dõi (0) 1 Trả lời -


Giải phương trình 2x/3+2x−1/6=4−x/3
bởi Nguyễn Thị An
 25/02/2019
25/02/2019
Giai phương trình : a ) \(\frac{2x}{3}+\frac{2x-1}{6}=4-\frac{x}{3}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình y (y - 1) ( y - 2) - y^2 + 1 = 0
bởi Hoa Hong
 25/02/2019
25/02/2019
GIẢI PHƯƠNG TRÌNH :
y ( y - 1) ( y - 2) - y^2 + 1 = 0
Theo dõi (0) 1 Trả lời -


giải phương trình :
\(\frac{x-12}{77}+\frac{x-11}{78}=\frac{x-74}{15}+\frac{x-73}{16}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình sau :
\(x+\frac{x}{x+2}+\frac{x+3}{x^2+5x+6}+\frac{x+4}{x^2+6x+8}=1\)
Theo dõi (0) 1 Trả lời -


Giải phương trình nghiệm nguyên y^2-x(x-2)(x^2-2x+2)=0
bởi minh dương
 25/02/2019
25/02/2019
giải phương trình nghiệm nguyên y^2-x(x-2)(x^2-2x+2)=0
Theo dõi (0) 1 Trả lời -


Giải phương trình sau 3x^3-8x^2-2x+4=0
bởi con cai
 25/02/2019
25/02/2019
Giải phương trình sau :
\(3x^3-8x^2-2x+4=0\)
Theo dõi (0) 1 Trả lời -


Giải phương trình x^3-4x^2+7x-6=0
bởi Nguyễn Tiểu Ly
 25/02/2019
25/02/2019
Giải phương trình :
\(x^3-4x^2+7x-6=0\)
Theo dõi (0) 1 Trả lời -


giải phương trình
(x2+3x-4)3+(3x2+7x+4)3=(4x2+10x)3
Theo dõi (0) 1 Trả lời -


giải phương trình :
(x+3/x-2)+6-(x-3/x+2)2-7(x2-9)/x2-4=0
Theo dõi (0) 1 Trả lời -


Giải phương trình (−x−4/7)−(5/3+11/4)=−5/6
bởi cuc trang
 25/02/2019
25/02/2019
Giải phương trình sau:
\(\left(-x-\frac{4}{7}\right)-\left(\frac{5}{3}+\frac{11}{4}\right)=\frac{-5}{6}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình (x^2+x)^2+4(x^2+x)=12
bởi Nguyễn Lệ Diễm
 25/02/2019
25/02/2019
giải phương trình : \(\left(x^2+x\right)^2+4\left(x^2+x\right)=12\)
Theo dõi (0) 1 Trả lời -


Giải phương trình 64 - 3 (x + 2) = 5x - 41
bởi Thanh Truc
 25/02/2019
25/02/2019
Giải phương trình sau:
64 - 3 (x + 2) = 5x - 41
Theo dõi (0) 1 Trả lời -


Giải phương trình 2−x/2007−1=1−x/2008−x/2009
bởi Anh Trần
 25/02/2019
25/02/2019
Giải phương trình sau:\(\frac{2-x}{2007}-1=\frac{1-x}{2008}-\frac{x}{2009}\)
Theo dõi (0) 1 Trả lời -


Tính cạnh của 1 hình vuông biết rằng nếu chu vi tăng 12 m thì diện tích tăng 135 m^2
bởi Aser Aser
 25/02/2019
25/02/2019
Các dạng toán giải phương trình (1)
Bài 1: Tính cạnh của 1 hình vuông biết rằng nếu chu vi tăng 12 m thì diện tích tăng 135 m2 ?
Bài 2: Tổng 2 số là 321. Tổng của \(\frac{5}{6 }\) số thứ nhất và 2,5 số kia bằng 21. Tìm 2 số đó?
Theo dõi (0) 1 Trả lời -


Chững minh bất đẳng thức
abc\(\ge\) (b+c-a)(a+c-b)(a+b-c)
với a,b,c là độ dài ba cạnh của một tam giác
Theo dõi (0) 1 Trả lời -


Phân tích đa thức thành nhan tử: ab( x2 - y2) - xy( a2 - b2)
Theo dõi (0) 1 Trả lời -


Tìm GTLN của biểu thức A=4x-x^2+3
bởi Lan Anh
 26/02/2019
26/02/2019
''Hép me'' nhé, cảm ơn bạn rất nhiều
Tìm GTLNN, GTLN (ÁP DỤNG VÀO HẰNG ĐẲNG THỨC ĐẤY)
A=4x-x2+3
B=2x2-6x
C=x-3x2
Theo dõi (0) 1 Trả lời -


Tìm x biết (3x-5)(x+1)-(x-1)(x+2)=(2x-3)(x+2)+1
bởi Lê Minh Trí
 26/02/2019
26/02/2019
cho mik hỏi vs
đây là dạng bài nhân đa thức vs đa thức ( tìm x biết)
(3x-5)(x+1)-(x-1)(x+2)=(2x-3)(x+2)+1
Theo dõi (0) 1 Trả lời -


Tìm x biết x^2-5x=0
bởi Lê Chí Thiện
 26/02/2019
26/02/2019
tìm x
a) x2 - 5x = 0
b) 3x ( x - 2 ) + 2( 2 - x ) = 0
c) 5x ( 3x - 1 ) + x( 3x - 1 ) - 2( 3x - 1) = 0
Theo dõi (0) 1 Trả lời -


Tính 3x^2(x + 1 ) - 2( x + 1 )
bởi Tay Thu
 26/02/2019
26/02/2019
4) 3x2(x + 1 ) - 2( x + 1 )
5) ( a + b + c )2 - ( ab + bc + ca )(a + b + c ) + ( a + b + c )
6) 4x2( x - 2y) - 20x( 2y - x)
7) 3x2y2 ( a - b + c ) + 2xy ( b - a - c )
Theo dõi (0) 1 Trả lời -


Tính 4x^3 - 14x^2
bởi Aser Aser
 26/02/2019
26/02/2019
1) 4x3 - 14x2
2) 5y10 + 15y6
3) 9x2y2 + 15x2y - 21xy2
Theo dõi (0) 1 Trả lời -


Thu gọn biểu thức sau:
a) (x+1).(x+2).(x2+4).(x-1).(x2+1).(x-2)
b) (3x+1)2+(2-3x).(2+3x)
Theo dõi (0) 1 Trả lời -


tìm số nguyên x biết rằng ( 3x -1 ) ( 4x -1 ) ( 5x -1 ) ( 6x -1 ) = 120
Theo dõi (0) 1 Trả lời -


Tính x^6-y^6
bởi Tran Chau
 26/02/2019
26/02/2019
\(x^6-y^6\)
Theo dõi (0) 1 Trả lời -


Tính 4x^2-25
bởi Trịnh Lan Trinh
 26/02/2019
26/02/2019
\(4x^2-25\)
Theo dõi (0) 1 Trả lời