Hình học 8 Bài 9: Thể tích của hình chóp đều - Luyện tập

+ Hình chóp là hình có mặt đáy là một đa giác và các mặt bên là các tam giác có chung đỉnh.

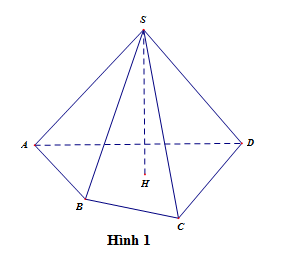
Trên hình 1 ta có hình chóp S.ACBD, \(SH \bot {\rm{mp}}\left( {ABCD} \right)\), S là đỉnh, SH là đường cao của hình chóp.

+ Hình chóp đều là hình chóp có mặt đáy là một đa giác đều, các mặt bên là những tam giác cân bằng nhau có chung đỉnh (là đỉnh của hình chóp đều).

Trên hình  ta có hình chóp tứ giác đều, SO là đường cao, O là tâm của đường tròn đi qua các đỉnh của lục giác ABCD.

Đường cao SK của mặt bên gọi là trung đoạn của hình chóp.

+ Khi cắt hình chóp đều bởi mộ mặt phẳng song song với đáy, phần hình chóp nằm giữa hai mặt phẳng đó và mặt phẳng đáy của hình chóp gọi là hình chóp cụt đều.

Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.

Trên hình 2, ta có hình chóp cụt tứ giác đều ABCD.A'B'C'D'.

Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy và trung đoạn.

\({S_{xq}} = p.d\)  (p là nửa chu vi đáy; d là trung đoạn của hình chóp đều).

+ Diện tích toàn phần của hình chóp bằng tổng của diện tích xung quanh và diện tích đáy.

+ Với hình chóp, để tính diện tích xung quanh ta tính tổng diện tích của các mặt bên.

+  Để tính diện tích xung quanh của hình chóp cụt đều, ta tính diện tích một mặt bên rồi nhân với số mặt bên, hoặc lấy diện tích xung quanh của hình chóp đều lớn trừ đi diện tích xung quanh của hình chóp đều nhỏ.

+  Thể tích của hình chóp đều bằng (\dfrac{1}{3}\) diện tích đáy nhân với chiều cao:  \(V = \dfrac{1}{3}S.h\)

( S là diện tích đáy, h là chiều cao)

+  Để tính thể tích của hình chóp cụt đều, ta lấy thể tích của hình chóp đều lớn trừ đi thể tích của hình chóp đều nhỏ.

Các dạng toán thường gặp

Dạng 1:  Xác định mối quan hệ giữa các yếu tố (cạnh, mặt phẳng…) trong hình chóp đều, hình chóp cụt đều.

Phương pháp:

+ Sử dụng mối quan hệ  song song và vuông góc giữa các đường thăng, các mặt phẳng, giữa đường thẳng và mặt phẳng.

+ Sử dụng kiến thức về hình chóp đều

Dạng 2: Tính độ dài cạnh, diện tích xung quanh, toàn phần và thể tích của hình chóp đều, hình chóp cụt đều.

Phương pháp:

Ta thường sử  dụng các công thức sau:

 + Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy và trung đoạn.

\({S_{xq}} = p.d\)  (p là nửa chu vi đáy; d là trung đoạn của hình chóp đều).

+ Diện tích toàn phần của hình chop bằng tổng của diện tích xung quanh và diện tích đáy.

+ Với hình chóp, để tính diện tích xung quanh ta tính tổng diện tích của các mặt bên.

+  Để tính diện tích xung quanh của hình chóp cụt đều, ta tính diện tích một mặt bên rồi nhân với số mặt bên, hoặc lấy diện tích xung quanh của hình chóp đều lớn trừ đi diện tích xung quanh của hình chóp đều nhỏ.

+  Thể tích của hình chóp đều bằng \(\dfrac{1}{3}\) diện tích đáy nhân với chiều cao  \(V = \dfrac{1}{3}S.h\)

( S là diện tích đáy, h là chiều cao)

+  Để tính thể tích của hình chóp cụt đều, ta lấy thể tích của hình chóp đều lớn trừ đi thể tích của hình chóp đều nhỏ.

Trên đây là bài học Hình học 8 Chương 4 Bài 9 Thể tích của hình chóp đều - Luyện tập và hướng dẫn Giải bài tập Hình học 8 Chương 4 Bài 9 sẽ giúp các em nắm được phương pháp giải các bài toán liên quan đến Thể tích của hình chóp đều - Luyện tập . Để củng cố kiến thức các em có thể làm bài kiểm tra Trắc nghiệm Hình học 8 Chương 4 Bài 9. Các em cũng có thể nêu thắc mắc của mình ở phần Hỏi đáp Hình học 8 Chương 4 Bài 9 để được giải đáp. Cộng đồng Toán HOC247 chúc các em học thật tốt bài học này.