Giải bài 44 tr 123 sách GK Toán 8 Tập 2
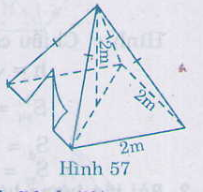
Hình 57 là một cái lều ở trại hè của học sinh kèm theo các kích thước. Thể tích không khí bên trong lều là bao nhiêu?
Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp…biết
(\(\sqrt{5} \approx 2,24\)).
Hướng dẫn giải chi tiết
Câu a:
Thể tích cần tính bằng thể tích của hình chóp có chiều cao \(2cm\), đáy là hình vuông cạnh dài \(2m\).
Diện tích đáy là:
\( S_{đ} = 2.2=4(m^2)\)
Thể tích hình chóp là:
\(V = \dfrac{1}{3}.S.h = \dfrac{1}{3}.4.2 = \dfrac{8}{3}\approx 2,67\)\(\,(m^3) \)
Câu b:
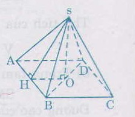
Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.
Gọi \(H\) là trung điểm của \(AB\) và \(O\) là tâm của hình vuông \(ABCD\).
Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao \(SH\) của mỗi mặt.
Theo định lý Pytago trong tam giác vuông SHA, ta có:
\(SH^2 =SO^2+OH^2 \)\(\,= SO^2+{\left( {\dfrac{{BC}}{2}} \right)^2} \) \(= 2^2+1^2=5\)
\( \Rightarrow SH =\sqrt{5}\approx 2,24(m) \)
Diện tích xung quanh của hình chóp là:
\( S_{xq} = p.d = \dfrac{1}{2}. 2.4.2,24 = 8,96 (m^2) \)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 45 trang 124 SGK Toán 8 Tập 2
Bài tập 46 trang 124 SGK Toán 8 Tập 2
Bài tập 47 trang 124 SGK Toán 8 Tập 2
Bài tập 48 trang 125 SGK Toán 8 Tập 2
Bài tập 49 trang 125 SGK Toán 8 Tập 2
Bài tập 50 trang 125 SGK Toán 8 Tập 2
Bài tập 62 trang 150 SBT Toán 8 Tập 2
Bài tập 63 trang 151 SBT Toán 8 Tập 2
Bài tập 64 trang 151 SBT Toán 8 Tập 2
Bài tập 65 trang 151 SBT Toán 8 Tập 2
Bài tập 66 trang 152 SBT Toán 8 Tập 2
Bài tập 67 trang 152 SBT Toán 8 Tập 2
Bài tập 68 trang 152 SBT Toán 8 Tập 2
Bài tập 69 trang 152 SBT Toán 8 Tập 2
Bài tập 70 trang 153 SBT Toán 8 Tập 2
-


tam giác ABC có trung tuyến AM=BC/2 . Chứng minh tam giác ABC vuông tại A
Theo dõi (0) 1 Trả lời -


Cho biết hình lập phương sau có cạnh bằng \(5\,\,cm\), thể tích của hình lập phương đó là:
bởi Suong dem
 15/07/2021
15/07/2021
A. \(125\,\,c{m^2}\)
B. \(25\,\,c{m^3}\)
C. \(25\,\,c{m^2}\)
D. \(125\,\,c{m^3}\)
Theo dõi (0) 1 Trả lời -


Giải: \(3x\left( {x - 2} \right) = {x^2} - 4\).
bởi Trần Phương Khanh
 14/07/2021
14/07/2021
Giải: \(3x\left( {x - 2} \right) = {x^2} - 4\).
Theo dõi (0) 1 Trả lời -


Cho biết tam giác \(ABC,\,\,AD\) là phân giác của \(\angle BAC\), biết \(AB = 16cm,\,\,AC = 24cm,\,\,DC = 15cm\). Khi đó \(BD\) bằng bao nhiêu?
bởi Vương Anh Tú
 14/07/2021
14/07/2021
A. \(10cm\) B. \(\dfrac{{128}}{5}cm\)
C. \(\dfrac{1}{{10}}cm\) D. \(\dfrac{{45}}{2}cm\)
Theo dõi (0) 1 Trả lời -
ADMICRO


Có tam giác \(ABC\) đồng dạng với tam giác \(MNP\) và \(\dfrac{{{S_{ABC}}}}{{{S_{MNP}}}} = 9\)
bởi Kim Ngan
 14/07/2021
14/07/2021
A. \(\dfrac{{MN}}{{AB}} = 9\) B. \(\dfrac{{MN}}{{AB}} = 3\)
C. \(\dfrac{{MN}}{{AB}} = \dfrac{1}{9}\) D. \(\dfrac{{MN}}{{AB}} = \dfrac{1}{3}\)
Theo dõi (0) 1 Trả lời -


Cho biết tam giác \(MNP\) đồng dạng với tam giác \(PQR\). Hệ thức đã cho nào sau đây không đúng?
bởi Nguyen Dat
 14/07/2021
14/07/2021
A. \(MN.QR = NP.PQ\)
B. \(MP.QR = NP.PR\)
C. \(MN.PQ = NP.QR\)
D. \(MN.PR = MP.PQ\)
Theo dõi (0) 1 Trả lời -


Với \(\Delta MNP\) có \(NQ\) là tia phân giác của góc \(MNP\). Biết \(MN = 3cm;\,\)\(NP = 5cm;\,\,\)\(MQ = 1,5cm\). Độ dài đoạn \(PQ\) bằng
bởi Tay Thu
 14/07/2021
14/07/2021
A. \(2,5cm\) B. \(3,5cm\)
C. \(4cm\) D. \(4,5cm\)
Theo dõi (0) 1 Trả lời -


Có \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH = 12cm\) và đường trung tuyến \(AM = 15cm\). Biết khẳng định nào sau đây là đúng?
bởi Hữu Nghĩa
 14/07/2021
14/07/2021
A. \(\frac{{AB}}{{AC}} = \frac{3}{5}\) B. \(\frac{{AB}}{{AC}} = \frac{2}{3}\)
C. \(\frac{{AB}}{{AC}} = \frac{3}{4}\) D. \(\frac{{AB}}{{AC}} = \frac{1}{2}\)
Theo dõi (0) 1 Trả lời -


Hãy cho biết hai đường chéo của một hình thoi bằng \(6cm\) và \(10cm\). Diện tích của hình thoi đó bằng:
bởi thanh hằng
 14/07/2021
14/07/2021
A. \(30c{m^2}\) B. \(60c{m^2}\)
C. \(32c{m^2}\) D. \(16c{m^2}\)
Theo dõi (0) 1 Trả lời -


Cho biết hình vuông có đường chéo là bằng \(4cm\), cạnh của hình vuông đó bằng:
bởi Naru to
 14/07/2021
14/07/2021
A. \(4\,\,cm\) B. \(8\,\,cm\)
C. \(\sqrt 8 \,\,cm\) D. \(2\,\,cm\)
Theo dõi (0) 1 Trả lời -


Cho hình thang \(ABCD\left( {AB\,{\rm{//}}\,CD} \right)\) biết \(\angle B = {65^0}\). Số đo góc \(C\) bằng bao nhiêu độ?
bởi Bo bo
 14/07/2021
14/07/2021
A. \({15^0}\) B. \({55^0}\)
B. C. \({65^0}\) D. \({115^0}\)
Theo dõi (0) 1 Trả lời -


Có \(\Delta ABC\), \(BD\) là tia phân giác của góc \(B\,\,\left( {D \in AC} \right)\), khi đó ta có:
bởi Nguyễn Hoài Thương
 15/07/2021
15/07/2021
A. \(\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}}\) B. \(\frac{{DA}}{{DC}} = \frac{{BD}}{{BC}}\)
C. \(\frac{{DA}}{{DC}} = \frac{{BC}}{{BA}}\) D. \(\frac{{DA}}{{DC}} = \frac{{BD}}{{BA}}\)
Theo dõi (0) 1 Trả lời -


Biết \(\Delta ABC\) đồng dạng với \(\Delta MNP\) theo trường hợp cạnh – góc – cạnh nếu có:
bởi Bảo Hân
 14/07/2021
14/07/2021
A. \(\angle B = \angle M;\,\,\frac{{CB}}{{MP}} = \frac{{AC}}{{NP}}\)
B. \(\angle A = \angle M;\,\,\angle B = \angle P\)
C. \(\angle A = \angle M;\,\,\frac{{AB}}{{MP}} = \frac{{AC}}{{NP}}\)
D. \(\angle A = \angle M;\,\,\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}\)
Theo dõi (0) 1 Trả lời -


Cho tứ giác \(ABCD\) nội tiếp một đường tròn tâm \(O\) và \(\angle BCD = {100^0}\). Số đo \(\angle DOB\) bằng đáp án?
bởi Ánh tuyết
 14/07/2021
14/07/2021
A. \({100^0}\) B. \({80^0}\)
C. \({160^0}\) D. \({40^0}\)
Theo dõi (0) 1 Trả lời -


Cho tam giác \(ABC\) vuông cân tại \(A\) nội tiếp đường tròn \(\left( O \right)\). Số đo cung nhỏ \(AC\) bằng bao nhiêu?
bởi thúy ngọc
 14/07/2021
14/07/2021
A. \({45^0}\) B. \({270^0}\)
C. \({120^0}\) D. \({90^0}\)
Theo dõi (0) 1 Trả lời -


Cho biết có một hình chữ nhật có chu vi bằng \(28m\), diện tích bằng \(48{m^2}\). Tìm các kích thước của hình chữ nhật đó.
bởi Nguyễn Hiền
 15/07/2021
15/07/2021
Cho biết có một hình chữ nhật có chu vi bằng \(28m\), diện tích bằng \(48{m^2}\). Tìm các kích thước của hình chữ nhật đó.
Theo dõi (0) 1 Trả lời -


Biết hình chóp tam giác đều \(S.ABC\) có thể tích bằng \(123,5c{m^3}\) và có cạnh đáy \(a = 10cm\). Chiều cao của hình chóp (lấy đến hai chữ số thập phân) là bằng:
bởi Bùi Anh Tuấn
 06/07/2021
06/07/2021
A. \(9,18cm\) B. \(9,17cm\)
C. \(8,56cm\) D. \(8,55cm\)
Theo dõi (0) 1 Trả lời -


Có hình chóp tứ giác đều có thể tích bằng \(34,5c{m^3}\) và có chiều cao là \(4,5cm\). Cạnh đáy của hình chóp (lấy đến hai chữ số thập phân) là bằng
bởi Nguyễn Hiền
 06/07/2021
06/07/2021
A. \(4,79cm\) B. \(4,80cm\)
C. \(5,39cm\) D. \(2,77cm\)
Theo dõi (0) 1 Trả lời -


Hình chóp tứ giác đều có cạnh đáy \(a = 15cm\) và chiều cao hình chóp là \(h = 12,5cm\). Hãy tính thể tích của hình chóp đã cho
bởi Nguyễn Thanh Hà
 06/07/2021
06/07/2021
A. \(937,5c{m^3}\) B. \(1050c{m^3}\)
C. \(781,25c{m^3}\) D. \(250c{m^3}\)
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABC đồng dạng tam giác HBA?
bởi Galph Kevin
 07/06/2020
07/06/2020
Giải bài toán
Cho tam giác ABC vuông tại A (AC > AB), đường cao AH
a) Chứng minh tam giác ABC đồng dạng tam giác HBA
b) Chứng minh AC^2=BC.HC
Theo dõi (0) 3 Trả lời -


Cho tam giác ABC vuông tại B đường cao BH. Tia phân giác góc B của tam giác BCD cắt AC tại D, phân giác góc A cắt các đoạn thẳng BH, BD, BC lần lượt tại I, K, F
bởi Lê Thị A
 26/05/2020
26/05/2020
a) ∆BCH ∾ ∆BAH
b) ∆IKB ∾ ∆IHS
Theo dõi (0) 0 Trả lời -


Cho ∆ABC vuông tại B, đường cao BH. Phân gia s góc B của ∆BCH cắt AC tại D, phân giác góc A cắt BH, BD, BC tại I, K, F
bởi Lê Thị A
 26/05/2020
26/05/2020
a) CM: ∆BCH ∾ ∆BAH
b) CM: ∆IKB ∾ ∆IHA
Theo dõi (1) 3 Trả lời -


Cho tam giác ABC vuông tại A, M thuộc AC. Từ C vẽ đường thẳng vuông góc với tia BM tại H, cắt tia BA tại O
bởi Lonhh Shhss
 26/05/2020
26/05/2020
a) CM: OA.OB=OH.OC
b) Cho góc ACB=38°, tính số đo góc OHA
c) Trên các đoạn thẳng BH và AC lấy lần lượt 2 điểm I và K sao cho OIC=OKB=90°. CM: OI=OK
Theo dõi (0) 0 Trả lời -


Cho tam giác MNP vuông tại M, trên cạnh MP lấy điểm A. Qua điểm A kẻ đường thẳng vuông góc với PN tại E
bởi Monkey.D Luffy
 24/05/2020
24/05/2020
a) Chúng minh tam giác EAP và tam giác MNP đồng dạng và PA . PM = PE . PN.
b) Chứng minh: Tam giác EPM đồng dạng với tam giác APN
c) Qua P kẻ đường thẳng vuông góc với tia NA tại B. Chứng minh hệ thức NA.NB = NE.NP, từ đó suy ra hệ thức NA.NB = PA.PM không đổi khi A di chuyển trên cạnh MP.
d) Chúng minh MA là tia phân giác của góc EMB
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC vuông ở A, D là 1 điểm tùy ý trên AC. Qua C kẻ tia Cx vuông góc với BD tại E. Kẻ AH vuông góc với BC tại H (H thuộc BC). Biết AB = 6cm, AC=8cm
bởi Uyen Nguyen
 22/05/2020
22/05/2020
a) Chứng minh:tam giác ADB đồng dạng với tam giác EDC
b) CHứng minh: tam giác ADE đồng dạng với tam giác BDC
c) Tính BH, AH
d) Qua A kẻ Ay vuông góc với AE, tia Ay cắt BD tại F. CHứng minh AE.BC=CA.EF; AB.CE+AE.BC=AC.BE
Theo dõi (0) 0 Trả lời -


Chứng minh rằng AB^2= BH.BC, suy ra độ dài các đoạn thẳng BH và CH biết tam giác ABC vuông tại A, AB=15cm, AC=20cm
bởi Nguyễn Ngọc Đàm
 18/05/2020
18/05/2020
Cho tam giác ABC vuông tại A, AB=15cm, AC=20cm. Kẻ đường cao AH của tam giác ABC
a. Chứng minh rằng AB^2= BH.BC, suy ra độ dài các đoạn thẳng BH và CH
b. Kẻ HM vuông góc AB và HN vuông góc AC. Chứng minh rằng AM.AB=AN.AC, suy ra tam giác AMN đồng dạng tam giác ACB
c. Tính tỉ số diện tích 2 tam giác AMN và ACB, suy ra diện tích tam giác AMN
Theo dõi (0) 0 Trả lời -


Chứng minh tam giác ABC đồng dạng với tam giác HBA từ đó suy ra AB.AC=AH.BC biết tam giác ABC vuông tại A
bởi Mỹ Mỹ
 17/05/2020
17/05/2020
cho tam giác ABC vuông tại A đường cao AH
a) chứng minh tam giác ABC đồng dạng với tam giác HBA từ đó suy ra AB.AC=AHBC
b) chứng minh AH^2 = HB.HC
c) phân giác ABC cắt AH và AC lần lượt tại I và K
chứng minh AI^2= IH.KCTheo dõi (0) 0 Trả lời -


Cho hình thang ABCD và 2 điểm M và N thuộc AD và BC sao cho AM/AD=BN/BC=2/3. Tính tỉ số Diện tích ABNM/ABCD
bởi Nguyễn Văn Quang
 10/05/2020
Theo dõi (0) 0 Trả lời
10/05/2020
Theo dõi (0) 0 Trả lời -


Tính chiều dài quãng đường từ Hà Nội đến Hải Dương
bởi Nguyễn Minh
 09/05/2020
09/05/2020
Bài 4. Cho tam giác ABC có AB = 9cm. Trên cạnh AB lấy điểm D sao cho AD = 6cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Tính độ dài AF.
Bài 5. Một ô tô và một xe máy cùng đi từ Hà Nội đến Hải Dương. Vận tốc trung bình của ô tô là 50km/h, vận tốc trung bình của xe máy là 30km/h. Để đi hết quãng đường từ Hà Nội đến Hải Dương, ô tô cần ít thời gian hơn xe máy là 1 giờ. Tính chiều dài quãng đường từ Hà Nội đến Hải Dương.Theo dõi (1) 5 Trả lời -


cho tam giác ICD vuông tại I,đường cao IK. a) Chứng minh: tam giác ICD và tam giác KCI đồng dạng với nhau.Tính IC,IK biết ID=12cm,CD=15cm. b)Chứng minh :IK ²=KC.KD c)Phân giác của góc IDF cắt IK tại E,cắt IC tại F.Tính tỉ số diện tích của tan giác IDF và tam giác KDE.
Theo dõi (0) 0 Trả lời -


Bài 3: Cho tam giác ABC có trọng tâm G, trung tuyến AM. Qua G vẽ đường thẳng song song với AB cắt BC tại E, và đường thẳng song với AC cắt BC tại F
Cm: BE = EF = FC
Theo dõi (0) 1 Trả lời -


Chứng minh: ∆ABC ∽ ∆MNP biết điểm O nằm bên trong ∆ABC có M, N, P là trung điểm của OA, OB, OC
bởi Nguyễn Ngọc Gia Hân
 04/05/2020
04/05/2020
Bài 1: Cho điểm O nằm bên trong ∆ABC. Gọi M, N, P theo thứ tự là trung điểm của OA, OB, OC.
a) Chứng minh: ∆ABC ∽ ∆MNP
b) Tính chu vi ∆MNP, biết chu vi ∆ABC bằng 88
mong m.n giúp đỡ ạ
Theo dõi (1) 4 Trả lời -


Cho tam giac ABC có AD là phân giác. Gọi H, K lần lượt là hình chiếu vuông góc của B và C trên tia AD
bởi Trường Nguyễn
 02/05/2020
02/05/2020
a)Chứng minh tam giac ABH đồng dạng với tam giac ACK;tam giac BDH đồng dạng với tam giac CDK.
b)Chứng minh AH.DK=AK.DH
c)Tính độ dài AH biết BD=4cm,CD=6cm,AK=12cm.
Theo dõi (0) 0 Trả lời -


Chứng minh rằng KH là tia phân giác góc AKC ?
bởi Ngũ Ngọc Thư Kỳ
 29/04/2020
29/04/2020
Cho tam giác ABC vuông tại A; K là trung điểm của BC. Trên tia đối của tia
KA lấy D, sao cho KD = KA.
a) Chứng minh: CD // AB.
b) Gọi H là trung điểm của AC; BH cắt AD tại M; DH cắt BC tại N.
Chứng minh: tam giác HMN cân.
c) Chứng minh rằng KH là tia phân giác góc AKC
Theo dõi (1) 1 Trả lời -


Chứng minh tam giác AHB đồng dạng tam giác BCD biết hình chữ nhật ABCD có AB=a=12cm, BC=b=9cm
bởi Lan Hương
 29/04/2020
29/04/2020
Cho hcn ABCD có AB=a=12cm, BC=b=9cm. Gọi H là chân đường vuông góc kẻ từ A xuống BD
a, chứng minh tgiac AHB đồng dạng tgiac BCD
b, tính độ dài đoạn thẳng AH
c., tính diện tích tam giác AHB
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC vuông tại A. Biết BC= 20cm và AB/AC=3/4
a) Tính AB,AC
b) Trên cạnh AB,AC lấy hai điểm D,E sao cho AD=3cm; CE=12 cm. Chứng minh DE//BC
Theo dõi (0) 3 Trả lời -


Chứng minh tam giác AMH đồng dạng tam giác AHB biết tam giác ABC có 3 góc nhọn, đường cao AH
bởi Giúp Tui zới
 24/04/2020
24/04/2020
Cho tam giác ABC có 3 góc nhọn, đường cao AH,vẽ HMvuông góc AB, HN vuông góc AC
a) Cm tg AMH đồng dạng tg AHB. Từ đó suy ra AH2=AM.AB
b) Cm rằng AM.AB=AN.AC
c) Cm tg ANM đồng dạng tg ABC
d)Gọi O là giao điểm AH với MN. Cm rằng OA.OH=OM.ON
Theo dõi (0) 1 Trả lời -


Hai địa điểm A và B cách nhau 400km , Lúc 6 giờ một xe máy khởi hành từ A về phía B với vận tốc 40 km/h . Sau đó 5 giờ một ô tô khởi hành từ B về phía A với vận tốc lớn hơn vận tốc xe máy là 20km/h. Hỏi hai xe gặp nhau lúc mấy giờ? Và địa điểm gặp nhau cách A bao nhiêu km ?
Giải giúp mình với ạ
Theo dõi (0) 0 Trả lời -


một oto chạy trên quãng đường AB. Lúc đi oto chạy với vận tốc trung bình 65km/h. Lúc về oto chạy với vận tốc trung bình 55km/h. Do đó thời gian đi ít hơn thời gian về 24 phút. Tính quãng đường AB
Theo dõi (0) 2 Trả lời -


x(x^2-4) = 0 và x(x-2)=0
Theo dõi (0) 2 Trả lời -


Cho tứ giác ABCD, AC và BD cắt nhau tại O. Đường thẳng qua O và song song BC cắt AB ở E; đường thẳng song song CD qua O cắt AD tại F. Chứng minh EG=FH
bởi Nguyễn Huy Khánh
 24/03/2020
24/03/2020
cho tứ giác ABCD,AC và BD cắt nhau tại O.Đường thẳng qua O và // BC cắt AB ở E:đường thẳng // CD qua O cắt AD tại F
a) EG=FH
b)Từ O kẻ các đường thẳng // AB,AD cắt BD,CD tại G và H
CMR:CG.DH=BG.CH
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC (AB vuông gócAC). Trên cạnh AC lấy điểm D sao cho CD = AB. Gọi E , F , G , H theo thứ tự là trung điểm của BC, AC, AD và BD. Chứng minh EF // GH và EF = GH
bởi bùi mạnh đức
 24/03/2020
24/03/2020
. Cho tam giác ABC (AB vuông gócAC). Trên cạnh AC lấy điểm D sao cho CD = AB. Gọi E , F , G , H theo thứ tự là trung điểm của BC, AC. AD và BD.
a/ Chứng minh EF // GH và EF = GH
b/ Chứng minh tứ giác EFGH là hình thoi
c/ Tia phân giác của góc A cắt BC tại M. Chứng minh AM vuông góc HF
Theo dõi (0) 7 Trả lời -


Cho tam giác ABC, G là trọng tâm. Qua G vẽ đường thẳng song song với cạnh AC, cắt các cạnh AB, BC lần lượt ở D và E. Tính độ dài đoạn thẳng DE, biết ADECcm16 và chu vi tam giác ABC bằng 75cm.
bởi Nấm Lùn Cute
 23/03/2020
23/03/2020
Cho tam giác ABC, G là trọng tâm. Qua G vẽ đường thẳng song song với cạnh AC, cắt
các cạnh AB, BC lần lượt ở D và E. Tính độ dài đoạn thẳng DE, biết ADECcm16 và
chu vi tam giác ABC bằng 75cm.
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vuông ở A (AB < AC), đường cao AH, biết AB = 6. Đường trunh trực của BC cắt các đường thẳng AB, AC, BC theo thứ tự ở D, E và F biết DE =5cm, EF = 4cm. Chứng minh: Tam giác FEC đồng dạng với tam giác FBD
bởi nguyễn duy hòa
 21/03/2020
21/03/2020
a, Tam giác FEC đồng dạng với tam giác FBD
b, Tam giác AED đồng dạng với tam giác HAC
c, tính BC, AH, AC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có 3 đường cao AD, BE, CF. H là giao điểm của 3 đường cao, H' là điểm đối xứng với H qua BC. M,N là hình chiếu của H' trên AB, AC. I là giao điểm của AD và EF. a> cm góc AEF = ABC
bởi Thuý Anh
 20/03/2020
20/03/2020
các bn lm giúp mk câu b ý 2, câu c bài này vs :
cho tam giác ABC có 3 đường cao AD, BE, CF , H là gđ của 3 đường cao , H' là điểm đối xứng vs H qua BC . M,N là hình chiếu của H' trên AB, AC . I là giao điểm của AD và EF .
a> cm góc AEF = ABC
b> cm EH là tia p/g của góc FED và M,D,N thẳng hàng
c> gọi S, S1 , S2 , S3 lần lượt là diện tích các tam giác ABC, AEF, BDF, CDEcm : (S1.S2.S3) / (S^3 ) < hoặc bằng 1/64
cảm ơn mn
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC vuông tại A, AD là phân giác của góc A(D thuộcBC). Gọi D là đường vuông góc kẻ từ D tới AB (E thuộc AB) DF là đường vuông góc kẻ từ D đến AC (F thuộc AC). O là trung điểm EF. Hỏi AEDF là hình gì? Vì sao?
bởi bùi mạnh đức
 19/03/2020
19/03/2020
Cho tam giác ABC vuông tại A, AD là phân giác của góc A(D thuộcBC). Gọi D là đường vuông góc kẻ từ D tới AB (E thuộc AB) DF là đường vuông góc kẻ từ D đến AC (F thuộc AC). O là trung điểm EF.
a/ AEDF là hình gì? Vì sao?
b/ C/m A,O,D thẳng hang
c/ Gọi MN lần lượt là trung điểm của BD và CD. Tứ giác MAFN là hình gì? Vì sao?
Theo dõi (0) 0 Trả lời -


Tính nhanh 1052 + 52 - 10.105
bởi Yas uo
 19/03/2020
19/03/2020
1052 + 52 - 10.105
Theo dõi (0) 2 Trả lời -


tìm x để các phân thức sau xác định:
A=9x^2-16/3x^2+5B=x^2+4x+4
Theo dõi (0) 3 Trả lời -


Phân tích các đa thức sau thành nhân tử : a) x2 - xy + 3x - 3y b) x3 + 2x2 + x c) 2x2 - 3x - 5
bởi Trần Lệ Thuỷ
 18/03/2020
18/03/2020
Phân tích các đa thức sau thành nhân tử :
a) x2 - xy + 3x - 3y
b) x3 + 2x2 + x
c) 2x2 - 3x - 5
Theo dõi (0) 7 Trả lời -


Cho ∆ABC,G là trọng tâm.Qua G vẽ đường thẳng song song với cạnh AC, cắt các cạnh AB,BC,lần lượt ở D và E. Tính độ dài đoạn thẳng DE,biết AD+EC=16cm và chu vi ∆ABC=75cm
bởi ̿nguyen quang hai ❦☯๖ۣۜ₢๖ۣۜ=ε/̵͇̿̿/'̿'̿ ̿ ̿̿
 18/03/2020
18/03/2020
Cho tam giác ABC, G là trọng tâm. Qua G vẽ đường thẳng song song với cạnh AC, cắt các
cạnh AB, BC lần lượt ở D và E. Tính độ dài đoạn thẳng DE, biết ADECcm16 và chu vi tam
giác ABC bằng 75cm.Theo dõi (0) 0 Trả lời -


Chứng minh: Diện tích hình vuông dựng trên cạnh góc vuông của một tam giác vuông cân gấp hai lần diện tích hình vuông dựng trên đường cao thuộc cạnh huyền.
bởi Trương Tấn Hoàng
 18/03/2020
18/03/2020
Chứng minh rằng:
a) Diện tích hình vuông dựng trên cạnh góc vuông của một tam giác vuông cân gấp hai lần diện tích hình vuông dựng trên đường cao thuộc cạnh huyền.
b) Diện tích hình vuông có cạnh là đường chéo của một hình chữ nhật thì lớn hơn hoặc bằng hai lần diện tích hình chữ nhật đó.
Theo dõi (0) 5 Trả lời -


Giải phương trình: 4x-10=0
bởi Lê Nguyên
 17/03/2020
17/03/2020
giải phương trình :4x-10=0
Theo dõi (1) 8 Trả lời -


X/2020+(X+1)/2021+(X+2)/2022+(X+3)/2023=4
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC. a) Gọi D là điểm đối cứng của A qua N. Chứng minh tứ giác ABCD là hình chữ nhật. b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I. Chứng minh tứ giác ANCE là hình thoi. c) Đường thẳng BC cắt DM và DI lần lượt tại G và G’. Chứng minh BG = CG’. d) Cho AB = 6cm, AC = 8cm. Tính diện tích ΔDGG’.
bởi jyurjdesgr5henrtj htdnrter
 16/03/2020
16/03/2020
Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.
a) Gọi D là điểm đối cứng của A qua N. Chứng minh tứ giác ABCD là hình chữ nhật.
b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I.
Chứng minh tứ giác ANCE là hình thoi.
c) Đường thẳng BC cắt DM và DI lần lượt tại G và G’. Chứng minh BG = CG’.
d) Cho AB = 6cm, AC = 8cm. Tính diện tích ΔDGG’.
Theo dõi (0) 0 Trả lời -


Cho hình thang ABCD có góc A bằng 90 độ, AB//CD, AB=AD=CD/2, BH là đường cao a) Chứng minh ABHD là hình vuông b) Tính số đo các góc B và C của hình thang
bởi Nguyễn An
 16/03/2020
16/03/2020
cho hình thang ABCD có góc A bằng 90 độ, AB//CD, AB=AD=CD/2, BH là đường cao
a) chứng minh ABHD là hình vuông
b) tính số đo các góc B và C của hình thang
c) gọi M là trung điểm của BC chứng minh MD=MD
Theo dõi (0) 0 Trả lời -


Giải phương trình: x^4-4x^3+12x-9=0
bởi Anh Lan
 15/03/2020
15/03/2020
x^4-4x^3+12x-9=0
Theo dõi (0) 1 Trả lời -


Tính (2x2 - 3x2 + 5x) : (x2 - x + 1)
bởi Nguyễn Quỳnh Trang
 15/03/2020
15/03/2020
(2x2 - 3x2 + 5x) : (x2 - x + 1)
Theo dõi (0) 1 Trả lời


