Giải bài 37 tr 79 sách GK Toán 8 Tập 2
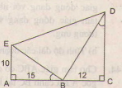
Hình 44 cho biết \(\widehat {EBA} = \widehat {BDC}\)
a) Trong hình vẽ, có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.
b) Cho biết AE = 10cm, AB = 15cm, BC = 12cn, Hãy tính độ dài các đoạn thẳng CD, BE, BD, ED(làm tròn đén chữ số thập phân thứ nhất).
c) So sánh diện tích tam giác BDE với tổng diện tích hai tam giác AEB và BCD.
Hướng dẫn giải chi tiết
Câu a:
Ta có: \(\widehat{EBA} = \widehat{BDC}\) (giả thiết) mà \(\widehat{BDC} + \widehat{CBD}={90^0}\) (do tam giác BCD vuông tại C)
\( \Rightarrow \widehat{EBA} + \widehat{CBD}={90^0}\)
Vậy \(\widehat{EBD} = {180^0} - (\widehat{EBA}+ \widehat{CBD})\)\(\, = {180^o} - {90^o} = {90^o}\)
Vậy trong hình vẽ có ba tam giác vuông đó là:
\(∆ABE, ∆CBD, ∆EBD.\)
Câu b:
\(∆ABE\) và \(∆CDB\) có:
\(\widehat{A} = \widehat{C}=90^o\)
\(\widehat{ABE}= \widehat{CDB}\) (giả thiết)
\( \Rightarrow ∆ABE ∽ ∆CDB\) (g-g)
\( \Rightarrow \dfrac{AB}{CD} = \dfrac{AE}{CB}\) (tính chất hai tam giác đồng dạng)
\( \Rightarrow CD = \dfrac{AB.CB}{AE} = 18\, (cm)\)
- Áp dụng định lí pitago ta có:
\( ∆ABE\) vuông tại \(A\)
\( \Rightarrow BE = \sqrt{AE^{2}+AB^{2}}\) \(\,=\sqrt{10^{2}+15^{2}}\) \( \approx 18\, (cm)\).
\(∆BCD\) vuông tại \(C\)
\( \Rightarrow BD = \sqrt {B{C^2} + D{C^2}} \) \(= \sqrt {{{12}^2} + {{18}^2}} \approx 21,6\,\,cm\)
\(∆EBD\) vuông tại \(B\)
\( \Rightarrow ED = \sqrt{EB^{2}+BD^{2}}\) \(=\sqrt{325+ 468} \approx 28,2\, (cm)\)
Câu c:
Ta có:
\(S_{ABE} + S_{DBC}\)
\(= \dfrac{1}{2}AE.AB + \dfrac{1}{2}BC.CD\)
\(= \dfrac{1}{2}. 10.15 + \dfrac{1}{2}.12.18\)
\(= 75 + 108 = 183\;cm^2\).
Ta có: \(A{\rm{E}}//DC\,\,\left(\text{ cùng } { \bot AC} \right) \Rightarrow \) \(ACDE\) là hình thang.
\(S_{ACDE} = \dfrac{1}{2}.(AE + CD).AC\)
\(= \dfrac{1}{2}.(10 + 18).27= 378\;cm^2\)
\( \Rightarrow S_{EBD} = S_{ACDE} - (S_{ABE}+ S_{DBC})\)\(\; = 378 - 183 = 195\,cm^2\)
\(S_{EBD}> S_{ABE} + S_{DBC}\) \(( 195 > 183)\).
Cách khác:
Các em có thể thay độ dài BE, BD tính được ở câu b để tính diện tích tam giác EBD.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 35 trang 79 SGK Toán 8 Tập 2
Bài tập 36 trang 79 SGK Toán 8 Tập 2
Bài tập 38 trang 79 SGK Toán 8 Tập 2
Bài tập 39 trang 79 SGK Toán 8 Tập 2
Bài tập 40 trang 80 SGK Toán 8 Tập 2
Bài tập 41 trang 80 SGK Toán 8 Tập 2
Bài tập 42 trang 80 SGK Toán 8 Tập 2
Bài tập 43 trang 80 SGK Toán 8 Tập 2
Bài tập 44 trang 80 SGK Toán 8 Tập 2
Bài tập 45 trang 80 SGK Toán 8 Tập 2
Bài tập 39 trang 93 SBT Toán 8 Tập 2
Bài tập 40 trang 93 SBT Toán 8 Tập 2
Bài tập 41 trang 93 SBT Toán 8 Tập 2
Bài tập 42 trang 94 SBT Toán 8 Tập 2
Bài tập 43 trang 94 SBT Toán 8 Tập 2
-


Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho DM là tia phân giác của BDE. Chọn khẳng định đúng.
bởi thuy tien
 16/01/2021
16/01/2021
A. góc ADE = góc AED
B. góc BDM = góc MEC
C. góc DEM = góc CEM
D. góc BMD = góc CME
Theo dõi (0) 1 Trả lời -


Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC, lấy D, E thuộc AB, AC sao cho góc DME = góc ABC. Tính BD.CE bằng
bởi Nguyễn Vân
 16/01/2021
16/01/2021
A. 2a2
B. 3a
C. a2
D. 4a2
Theo dõi (0) 1 Trả lời -


A. 18cm
B. 20cm
C. 15cm
D. 9cm
Theo dõi (0) 1 Trả lời -


A. 30cm
B. 20cm
C. 25cm
D. 15cm
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho hình bình hành ABCD có I là giao điểm của AC và BD. E là một điểm bất kì thuộc BC, qua E kẻ đường thẳng song song với AB và cắt BD, AC, AD tại G, H, F. Chọn kết luận sai?
bởi Nguyễn Anh Hưng
 16/01/2021
16/01/2021
A. ΔBGE ~ ΔHGI
B. ΔGHI ~ ΔBAI
C. ΔBGE ~ ΔDGF
D. ΔAHF ~ ΔCHE
Theo dõi (0) 1 Trả lời -


Cho hình bình hành ABCD, điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn khẳng định sai.
bởi Meo Thi
 15/01/2021
15/01/2021
A. ΔBFE ~ ΔDAE
B. ΔDEG ~ ΔBEA
C. ΔBFE ~ ΔDEA
D. ΔDGE ~ ΔBAE
Theo dõi (0) 1 Trả lời


