Giải bài 43 tr 94 sách BT Toán lớp 8 Tập 2
Chứng minh rằng, nếu hai tam giác \(ABC\) và \(A’B’C’\) đồng dạng với nhau thì:
a) Tỉ số của hai đường phân giác tương ứng bằng tỉ số đồng dạng.
b) Tỉ số của hai trung tuyến tương ứng bằng tỉ số đồng dạng.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.
- Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
Lời giải chi tiết
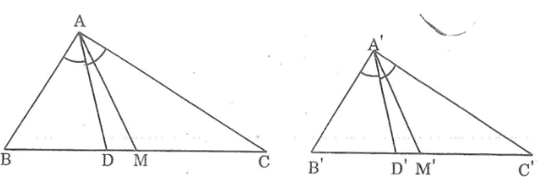
a)
Gọi \(AD\) là phân giác của góc \(A\) của \(∆ ABC\), \(A'D'\) là phân giác của góc \(A'\) của \(∆ A'B'C'\).
Giả sử \(∆ A’B’C’ \backsim ∆ ABC\) theo tỉ số \(k\) ta có:
\(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\) và \(\displaystyle {{A'B'} \over {AB}} = k\)
Mà \(\displaystyle \widehat {BAD} = {1 \over 2}\widehat A\) (vì \(AD\) là phân giác góc \(A\)) và \(\displaystyle \widehat {B'A'D'} = {1 \over 2}\widehat A\) (vì \(A'D'\) là tia phân giác góc \(A'\)).
\( \Rightarrow \widehat {BAD} = \widehat {B'A'D'}\)
Xét \(∆ ABD\) và \(∆ A’B’D’\) có:
+) \(\widehat B = \widehat {B'}\) (chứng minh trên )
+) \(\widehat {BAD} = \widehat {B'A'D'}\) (chứng minh trên )
\( \Rightarrow ∆ ABD \backsim ∆ A’B’D’ \) (g.g)
\( \displaystyle \Rightarrow {{A'D'} \over {AD}} = {{A'B'} \over {AB}} = k\).
b) Gọi \(AM\) là đường trung tuyến ứng với cạnh \(BC\) của \(∆ ABC\), \(A'M'\) là đường trung tuyến ứng với cạnh \(B'C'\) của \(∆ A’B’C’\).
Giả sử \(∆ A’B’C’ \backsim ∆ ABC\) theo tỉ số \(k\) ta có: \(\displaystyle {{A'B'} \over {AB}}={{B'C'} \over {BC}} = k\)
Mà \(\displaystyle B'M' = {1 \over 2}B'C'\) (vì \(M\) là trung điểm \(BC\)) và \(\displaystyle BM = {1 \over 2}BC\) (vì \(M'\) là trung điểm \(B'C'\)) nên \(\displaystyle {{B'M'} \over {BM}}= \dfrac{{\dfrac{1}{2}B'C'}}{{\dfrac{1}{2}BC}} = \dfrac{{B'C'}}{{BC}} = k\)
Xét \(∆ ABM\) và \(∆ A’B’M’\) có:
+) \(\displaystyle {{A'B'} \over {AB}} = {{B'M'} \over {BM}} = k\)
+) \(\displaystyle \widehat B = \widehat {B'}\) (chứng minh trên )
\( \Rightarrow ∆ ABM \backsim ∆ A’B’M’\) (c.g.c)
\( \displaystyle \Rightarrow {{A'M'} \over {AM}} = {{A'B'} \over {AB}} = k\).
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Cho tam giác ABC, Điểm D thuộc cạnh BC sao cho BD=1/2DC. Kẻ BH và CK vuông góc với AD. Chứng minh BH=1/2CK
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABO đồng dạng với DCO biết tứ giác ABCD có A=B=90 độ
bởi Nguyễn Vũ Khúc
 25/02/2019
25/02/2019
Tứ giác ABCD Có góc A = góc B=90 độ gọi O là giao điểm của AC và BD biết góc BAO = góc BDC chứng minh a) ∆ABO~ ∆DCO. b) BC. DO=CO.AD
Theo dõi (0) 1 Trả lời -


Chứng minh FK=AD biết FK vuông góc BE tại K
bởi khanh nguyen
 06/11/2018
06/11/2018
Cho tam giác ABC nhọn, vẽ đường thẳng xy qua A và song song với BC. Từ B vẽ BD vuông góc với AC ở D, BD cắt xy tại E. Trên tia BC lấy F sao cho BF=AE
a.Chướng minh rằng EF=AB và EF sonh song AB
b.Từ F vẽ FK vuông góc BE tại K. CM FK=AD
Giúp mình với!!!
cảm ơn trước nhé!!!!
Theo dõi (0) 1 Trả lời -


Giải giúp mình câu C nhé các bạn. Cảm ơn nhiều
Cho tam giác ABC vuông tai A có AB=6 cm; AC=8cm. Kẻ đường cao AH (H thuộc BC)
a. chứng minh tam giác ABC đồng dạng vs TG HBA. Tính độ dài BC;AH
b. chứng minh AH2 = HB.HC
c. Gọi P là trung điểm của BH và Q là trung điểm của AH ; chứng minh AP vuông góc với CQ
Theo dõi (0) 3 Trả lời -
ADMICRO


Tính đường cao tương ứng với cạnh 26 cm biết tổng đường cao của hai cạnh tương ứng
bởi Việt Long
 12/04/2019
12/04/2019
Các bn ơi giúp k với mk sắp thi rùi,giúp mk mấy bài này nhé!

1,Số các giá trị nguyên x thỏa mãn: 3x ( |x| - 4)( x4 - 81)=0
2,Độ dài 3 cạnh của 1 tam giác tỉ lệ với 2,3,5.Ba chiều cao tương ứng với 3 cạnh đó tỉ lệ với 3 số nào?
3,Một người đi từ A đến B mật 5 giờ.Khi từ B về người nay đi nhanh hơn trước 2 km/h nên thời gian ít hơn là 40 p.Tính quãng đg AB
4,cho (x-y) : (x+y) : xy = 1: 7 : 24 (xy khác 0).Tính xy
5,Hai cạnh của 1 tam giác dài 26 cm và 35 cm.Tổng đường cao của hai cạnh tương ứng với 2 cạnh đó là 48,8 cm.Đường cao tương ứng với cạnh 26 cm là:
Theo dõi (0) 2 Trả lời -


Cho tam giác ABC có BC = 2AB. Gọi M là trung điểm của BC và D là trung điểm của BM. Chứng minh rằng AC = 2AD.
Theo dõi (0) 1 Trả lời



