Hoạt động 3 trang 73 SGK Toán 10 Kết nối tri thức tập 2
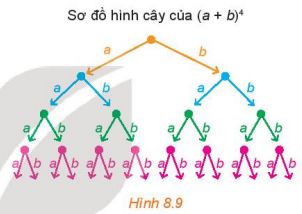
Sơ đồ hình cây của khai triển (a + b)4 được mô tả như Hình 8.9. Sau khi khai triển, ta thu được một tổng gồm 24 (theo quy tắc nhân) đơn thức có dạng x.y.z.t, trong đó mỗi x, y, z, t là a hoặc b. Chẳng hạn, nếu x, y, t là a, còn z là b thì ta có đơn thức a.a.b.a, thu gọn là a3b. Để có đơn thức này, thì trong 4 nhân tử x, y, z, t có 1 nhân tử là b, 3 nhân tử còn lại là a. Khi đó số đơn thức đồng dạng với 3b trong tổng là $C_{4}^{1}$.
Lập luận tương tự trên, dùng kiến thức về tổ hợp, hã̃y cho biết trong tổng nêu trên, có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau:
+) a4 +) a3b +) a2b2 +) ab3 +) b4
Hướng dẫn giải chi tiết
Phương pháp giải
Sử dụng công thức tổ hợp
Ví dụ Để có đơn thức a4 thì phải có 4 nhân tử a, khi đó số đơn thức đồng dạng là: \(C_{4}^{4}\) =1, hay có 1 đơn thức a4.
Tính tương tụ với a3b, a2b2, ab3, b4
Lời giải chi tiết
+) Để có đơn thức a4 thì phải có 4 nhân tử a, khi đó số đơn thức đồng dạng là: \(C_{4}^{4}\) =1, hay có 1 đơn thức a4.
+) Để có đơn thức a3b thì phải có 3 nhân tử a, 1 nhân tử b, khi đó số đơn thức đồng dạng là: \(C_{4}^{1}\) =4.
+) Để có đơn thức a2b2 thì có 2 nhân tử a, 2 nhân tử b, khi đó số đơn thức đồng dạng là: \(C_{4}^{2}\) = 6
+) Để có đơn thức ab3 thì có 1 nhân tử a, 3 nhân tử b, khi đó số đơn thức đồng dạng là: \(C_{4}^{3}\) = 4.
+) Để có đơn thức b4 thì phải có 4 nhân tử b, khi đó số đơn thức đồng dạng là: \(C_{4}^{4}\) =1, hay có 1 đơn thức b4.
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Hoạt động 1 trang 72 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Hoạt động 2 trang 72 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Luyện tập 1 trang 73 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Hoạt động 4 trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Luyện tập 2 trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Vận dụng trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.12 trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.13 trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.14 trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.15 trang 75 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.16 trang 75 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.13 trang 57 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.14 trang 57 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.15 trang 57 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.16 trang 57 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.17 trang 57 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
-


Trong khai triển \({\left( {1 + ax} \right)^n}\) ta có số hạng đầu là \(1\), số hạng thứ hai là \(24x\), số hạng thứ ba là \(252{x^2}\). Tìm \(a\) và \(n\).
bởi Dương Minh Tuấn
 13/09/2022
Theo dõi (0) 1 Trả lời
13/09/2022
Theo dõi (0) 1 Trả lời