Hoạt động 1 trang 72 SGK Toán 10 Kết nối tri thức tập 2
Hãy xây dựng sơ đồ hình cây của tích hai nhị thức (a+b).(c+d) như sau:
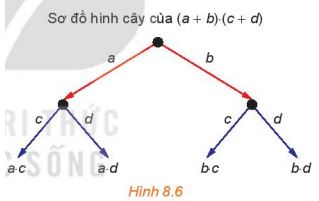
- Từ một điểm gốc, kẻ các mũi tên, mỗi müi tên tương ứng với một đơn thức (gọi là nhãn của mũi tên) của nhị thức thứ nhất (H.8.6);
- Từ ngọn của mỗi mũi tên đã xây dựng, kẻ các mũi tên, mỗi müi tên tương ứng với một đơn thức của nhị thức thứ hai;
- Tại ngọn của các mũi tên xây dựng tại bước sau cùng, ghi lại tích của các nhã̉n của các mũi tên đi từ điểm gốc đến đầu mút đó.
Hãy lấy tổng của các tích nhận được và so sánh kết quả với khai triển của tích (a+b).(c+d)
Hướng dẫn giải chi tiết
Phương pháp giải
Xác định Tổng các tích nhận được
Thực hiện khai triển của tích (a+b).(c+d)
Lời giải chi tiết
Tổng các tích nhận được: a.c + a.d + b.c + c.d
Khai triển của tích (a+b).(c+d) = a.c + a.d + b.c + c.d
Vậy tổng của các tích nhận được bằng với khai triển của tích (a+b).(c+d)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Hoạt động 2 trang 72 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Hoạt động 3 trang 73 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Luyện tập 1 trang 73 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Hoạt động 4 trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Luyện tập 2 trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Vận dụng trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.12 trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.13 trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.14 trang 74 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.15 trang 75 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.16 trang 75 SGK Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.13 trang 57 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.14 trang 57 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.15 trang 57 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.16 trang 57 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
Giải bài 8.17 trang 57 SBT Toán 10 Kết nối tri thức tập 2 - KNTT
-


Trong khai triển của \({\left( {x + a} \right)^3}{\left( {x - b} \right)^6}\), hệ số của \({x^7}\) là \( - 9\) và không có số hạng chứa \({x^8}\). Hãy tìm \(a\) và \(b\).
bởi Nguyen Ngoc
 14/09/2022
Theo dõi (0) 1 Trả lời
14/09/2022
Theo dõi (0) 1 Trả lời