Bài tập 4 trang 70 SGK Hình học 10 NC

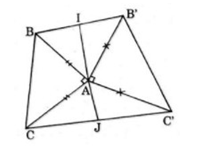
Trên hình 63 có vẽ hai tam giác vuông cân ABC và A'B'C' có chung đỉnh A. Gọi I và J lần lượt là trung điểm của hai đoạn thẳng BB' và CC'. Chứng minh rằng

a) AI⊥CC′, AJ⊥BB′;

b) BC′⊥B′C.

Hướng dẫn giải chi tiết

a) Ta có:

\(\begin{array}{l}
\overrightarrow {AI} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AB'} } \right);\overrightarrow {AJ} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AC'} } \right)\\
\Rightarrow \overrightarrow {AI} .\overrightarrow {CC'} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AB'} } \right).\left( {\overrightarrow {AC'} - \overrightarrow {AC} } \right)\\
= \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AC'} - \overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {AB'} .\overrightarrow {AC'} - \overrightarrow {AB'} .\overrightarrow {AC} } \right)
\end{array}\)

Vì AB⊥AC, AB′⊥AC′

Nên \(\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB'} .\overrightarrow {AC'} = 0\)

Mặt khác

\(\begin{array}{*{20}{l}}
{\overrightarrow {AB} .\overrightarrow {AC'} = AB.AC'.\cos BAC'}\\
{\overrightarrow {AB'} .\overrightarrow {AC} = AB'.AC.\cos B'AC}\\
\begin{array}{l}
\Rightarrow \overrightarrow {AB} .\overrightarrow {AC'} = \overrightarrow {AB'} .\overrightarrow {AC} \\
\Rightarrow \overrightarrow {AI} .\overrightarrow {CC'} = 0 \Rightarrow AI \bot CC'
\end{array}
\end{array}\)

Tương tự

\(\begin{array}{*{20}{l}}
{\overrightarrow {AJ} .\overrightarrow {BB'} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AC'} } \right).\left( {\overrightarrow {AB'} - \overrightarrow {AB} } \right)}\\
{ = \frac{1}{2}\left( {\overrightarrow {AC} .\overrightarrow {AB} - \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {AC'} .\overrightarrow {AB'} - \overrightarrow {AC'} .\overrightarrow {AB} } \right) = 0}\\
{ \Rightarrow AJ \bot BB'}
\end{array}\)

\(\begin{array}{*{20}{l}}
{\overrightarrow {BC'} .\overrightarrow {B'C} = \left( {\overrightarrow {AC'} - \overrightarrow {AB} } \right).\left( {\overrightarrow {AC} - \overrightarrow {AB'} } \right)}\\
{ = \overrightarrow {AC'} .\overrightarrow {AC} - \overrightarrow {AC'} .\overrightarrow {AB'} - \overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {AB} .\overrightarrow {AB'} }\\
{\overrightarrow {AB} .\overrightarrow {AB'} = AB.AB'.\cos BAB'}\\
\begin{array}{l}
\overrightarrow {AC} .\overrightarrow {AC'} = AC.AC'.\cos \left( {{{180}^0} - BAB'} \right)\\
= - \overrightarrow {AB} .\overrightarrow {AB'}
\end{array}
\end{array}\)

Do đó \(\overrightarrow {BC'} .\overrightarrow {B'C'} = 0\)

Vậy BC′⊥B′C.

-- Mod Toán 10 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 4 trang 70 SGK Hình học 10 NC HAY thì click chia sẻ