Bài tập 12 trang 73 SGK Hình học 10 NC
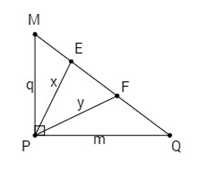
Cho tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc MPE, EPF, FPQ bằng nhau.
Đặt \(MP = q,\,PQ = m,\,PE = x,\,PF = y\) (h.64).
Trong các hệ thức sau, hệ thức nào đúng ?
(A) \(ME = EF = FQ\);
(B) \(M{E^2} = {q^2} + {x^2} - xq\);
(C) \(M{F^2} = {q^2} + {y^2} - yq\);
(D) \(M{Q^2} = {q^2} + {m^2} - 2qm\).
Hướng dẫn giải chi tiết
Đáp án A: ME, EF, FQ chưa chắc bằng nhau nên A sai.
Đáp án B:
\(\begin{array}{l}
M{E^2} = P{M^2} + P{E^2} - 2PM.PE\cos {30^0}\\
= {q^2} + {x^2} - 2qx.\frac{{\sqrt 3 }}{2}\\
= {q^2} + {x^2} - \sqrt 3 qx
\end{array}\)
nên B sai.
Đáp án C:
Ta có \(M{F^2} = M{P^2} + F{P^2} - 2.MP.FP.\cos \widehat {MPF}\)
\(= {q^2} + {y^2} - 2.q.y.\cos {60^0} \)
\(= {q^2} + {y^2} - qy.\)
nên C đúng.
Đáp án D: \(M{Q^2} = P{M^2} + P{Q^2} = {q^2} + {m^2}\) nên D sai.
Chọn (C).
-- Mod Toán 10 HỌC247
Bài tập SGK khác
-
Tam giác \(ABC\) có \(AB = 8cm,\,\,AC = 20cm\) và có diện tích bằng \(64c{m^2}\). Giá trị \(\sin A\) bằng bao nhiêu?
bởi An Vũ
16/07/2021
A. \(\sin A = \dfrac{{\sqrt 3 }}{2}\) B. \(\sin A = \dfrac{8}{9}\) C. \(\sin A = \dfrac{4}{5}\) D. \(\sin A = \dfrac{3}{8}\)
Theo dõi (0) 1 Trả lời -
Trong hệ tọa độ \(Oxy\), ta cho ba điểm \(A\left( {1;1} \right)\,,\,\,B\left( {2; - 1} \right)\,,\,\,C\left( {4;3} \right)\). Tọa độ điểm \(D\) để \(ABDC\) là hình bình hành là :
bởi Anh Thu
16/07/2021
A. \(D\left( {1;3} \right)\) B. \(D\left( {3;5} \right)\) C. \(D\left( {3;1} \right)\) D. \(D\left( {5;1} \right)\)
Theo dõi (0) 1 Trả lời -
Biết vectơ nào dưới đây là một vectơ pháp tuyến của \(d:\left\{ \begin{array}{l}x = - 1 + 2t\\y = 3 + t\end{array} \right.\)
bởi Lê Nhật Minh
16/07/2021
A. \(\overrightarrow {{n_1}} = \left( {2; - 1} \right)\) B. \(\overrightarrow {{n_3}} = \left( {1; - 2} \right)\) C. \(\overrightarrow {{n_2}} = \left( {1;2} \right)\) D. \(\overrightarrow {{n_4}} = \left( {1;2} \right)\)
Theo dõi (0) 1 Trả lời
