Giải bài 3.41 tr 76 SBT Toán 10
Giải và biện luận các phương trình sau theo tham số m:
a) \(2m\left( {x - 2} \right) + 4 = \left( {3 - {m^2}} \right)x\)
b) \(\frac{{\left( {m + 3} \right)x}}{{2x - 1}} = 3m + 2\)
c) \(\frac{{8mx}}{{x + 3}} = \left( {4m + 1} \right)x + 1\)
d) \(\frac{{\left( {2 - m} \right)x}}{{x - 2}} = \left( {m - 1} \right)x - 1\)
Hướng dẫn giải chi tiết
a) \(2m\left( {x - 2} \right) + 4 = \left( {3 - {m^2}} \right)x \Leftrightarrow \left( {m - 1} \right)\left( {m + 3} \right) = 4\left( {m - 1} \right)\)
- Với m ≠ 1 và m ≠ -3 phương trình có nghiệm \(x = \frac{4}{{m + 3}}\)
- Với m = 1 mọi số thực x đều là nghiệm của phương trình;
- Với m = -3 phương trình vô nghiệm.
b) ĐKXĐ: \(x \ne \frac{1}{2}\). Khi đó ta có:
\(\begin{array}{l}
\frac{{\left( {m + 3} \right)x}}{{2x - 1}} = 3m + 2 \Leftrightarrow \left( {m + 2} \right)x = \left( {3m + 2} \right)\left( {2x - 1} \right)\\
\Leftrightarrow \left( {5m + 1} \right)x = 3m + 2
\end{array}\)
Nếu m ≠ \( - \frac{1}{5}\) thì phương trình có nghiệm \(x = \frac{{3m + 2}}{{5m + 1}}\)
Giá trị này là nghiệm của phương trình đã cho khi
\(\frac{{3m + 2}}{{5m + 1}} \ne \frac{1}{2} \Leftrightarrow 6m + 4 \ne 5m + 1 \Rightarrow m \ne - 3\)
Nếu m = \( - \frac{1}{5}\) phương trình cuối vô nghiệm.
Kết luận:
Với m = \( - \frac{1}{5}\) hoặc m = -3 phương trình đã cho vô nghiệm.
Với m ≠ \( - \frac{1}{5}\)và m ≠ -3 nghiệm của phương trình đã cho là \(x = \frac{{3m + 2}}{{5m + 1}}\)
c) ĐKXĐ là x ≠ - 3. Khi đó ta có
\(\begin{array}{l}
\frac{{8mx}}{{x + 3}} = \left( {4m + 1} \right)x + 1 \Leftrightarrow 8mx = \left[ {\left( {4m + 1} \right)x + 1} \right]\left( {x + 3} \right)\\
\Leftrightarrow \left( {4m + 1} \right){x^2} + 4\left( {m + 1} \right)x + 3 = 0\,\,\,\left( 1 \right)
\end{array}\)
- Với m = \( - \frac{1}{4}\) phương trình (1) trở thành 3x + 3 = 0 ⇔ x = -1
- Với m ≠ \( - \frac{1}{4}\) phương trình (1) là một phương trình bậc hai có Δ' = (2m - 1)2 ≥ 0
Lúc đó phương trình (1) có hai nghiệm
\({x_1} = - \frac{3}{{4m + 1}},{x_2} = - 1\)
Ta có \( - \frac{3}{{4m + 1}} - 3 \Leftrightarrow 4m + 1 \ne 1 \Leftrightarrow m \ne 0\)
Kết luận:
Với m = 0 hoặc m = \( - \frac{1}{4}\) phương trình đã cho có một nghiệm x = -1.
Với m ≠ 0 và m ≠ \( - \frac{1}{4}\) phương trình đã cho có hai nghiệm x = -1 và \(x = - \frac{3}{{4m + 1}}\)
d) ĐKXĐ: x ≠ 2. Khi đó ta có
\(\begin{array}{l}
\frac{{\left( {2 - m} \right)x}}{{x - 2}} = \left( {m - 1} \right)x - 1 \Leftrightarrow \left( {2 - m} \right)x = \left( {x - 2} \right)\left[ {\left( {m - 1} \right)x - 1} \right]\\
\Leftrightarrow \left( {m - 1} \right){x^2} - \left( {m + 1} \right)x + 2 = 0\,\,\,\left( 2 \right)
\end{array}\)
- Với m = 1 phương trình (2) có dạng - 2x + 2 = 0 ⇔ x = 1
- Với m ≠ 1 thì phương trình (2) là một phương trình bậc hai có : Δ = (m - 3)2 ≥ 0
Lúc đó phương trình (2) có hai nghiệm
\({x_1} = 1,{x_2} = \frac{2}{{m - 1}}\)
Ta có \(\frac{2}{{m - 1}} \ne 2 \Leftrightarrow m - 1 \ne 1 \Leftrightarrow m \ne 2\)
Kết luận :
Với m = 1 và m = 2 phương trình đã cho có một nghiệm là x = 1.
Với m ≠ 1 và m ≠ 2 phương trình đã cho có hai nghiệm \(x= 1, x = \frac{2}{{m - 1}}\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 3.39 trang 76 SBT Toán 10
Bài tập 3.40 trang 76 SBT Toán 10
Bài tập 3.42 trang 76 SBT Toán 10
Bài tập 3.43 trang 76 SBT Toán 10
Bài tập 3.44 trang 77 SBT Toán 10
Bài tập 3.45 trang 77 SBT Toán 10
Bài tập 3.46 trang 77 SBT Toán 10
Bài tập 3.47 trang 77 SBT Hình 10
Bài tập 3.48 trang 77 SBT Toán 10
Bài tập 3.49 trang 77 SBT Toán 10
Bài tập 3.50 trang 77 SBT Toán 10
Bài tập 3.51 trang 77 SBT Toán 10
Bài tập 3.52 trang 77 SBT Toán 10
Bài tập 3.53 trang 78 SBT Toán 10
Bài tập 50 trang 101 SGK Toán 10 NC
Bài tập 51 trang 101 SGK Toán 10 NC
Bài tập 52 trang 101 SGK Toán 10 NC
Bài tập 53 trang 101 SGK Toán 10 NC
Bài tập 54 trang 101 SGK Toán 10 NC
Bài tập 55 trang 101 SGK Toán 10 NC
Bài tập 56 trang 101 SGK Toán 10 NC
Bài tập 57 trang 101 SGK Toán 10 NC
Bài tập 58 trang 102 SGK Toán 10 NC
Bài tập 59 trang 102 SGK Toán 10 NC
Bài tập 60 trang 102 SGK Toán 10 NC
Bài tập 61 trang 102 SGK Toán 10 NC
Bài tập 62 trang 102 SGK Toán 10 NC
-


Có bao nhiêu giá trị m nguyên để pt -x^2+4x+2-m=0 có 2 nghiệm phân biệt thuộc (-2;4)?
bởi Pham Thu Hien
 10/01/2020
Mọi người giải giúp mình với ạ, mai mình thi rồiTheo dõi (0) 0 Trả lời
10/01/2020
Mọi người giải giúp mình với ạ, mai mình thi rồiTheo dõi (0) 0 Trả lời -


có bao nhiêu giá trị m nguyên đê phương trình có nghiệm
Theo dõi (0) 0 Trả lời -


Tìm giá trị nhỏ nhất của P=x^2y^2+x^2-2xy-4x+1
bởi Phạm Anh
 06/01/2020
06/01/2020
Tìm giá trị nhỏ nhất của
Theo dõi (0) 1 Trả lời -


Giải phương trình |2x+1|=|x-2|
bởi Lâm Phương Châm
 03/01/2020
Phương trình chứa dấu trị tuyệt đối
03/01/2020
Phương trình chứa dấu trị tuyệt đối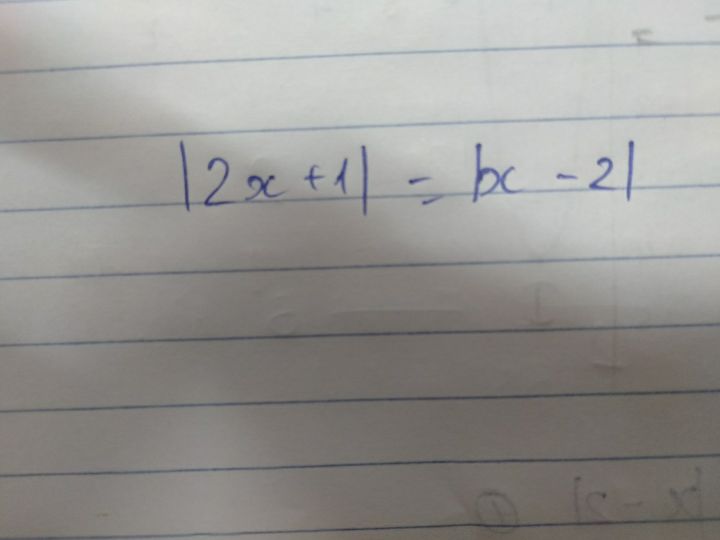 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -
ADMICRO


giải phương trình
căn2x+3+cănx+1 = 3x+2 *căn2x^2-5x+3 -16
Theo dõi (0) 0 Trả lời -


Giải phương trình 6 căn(1-x)-x=5 căn(1-căn(1-x))
bởi Minh Tuấn
 01/01/2020
01/01/2020
 Ai giúp mình với ạ. Đang cần gấp mai thiTheo dõi (0) 3 Trả lời
Ai giúp mình với ạ. Đang cần gấp mai thiTheo dõi (0) 3 Trả lời -


Giải phương trình x^2+căn(x^2-6)=12
bởi Hoa Nguyên
 01/01/2020
01/01/2020
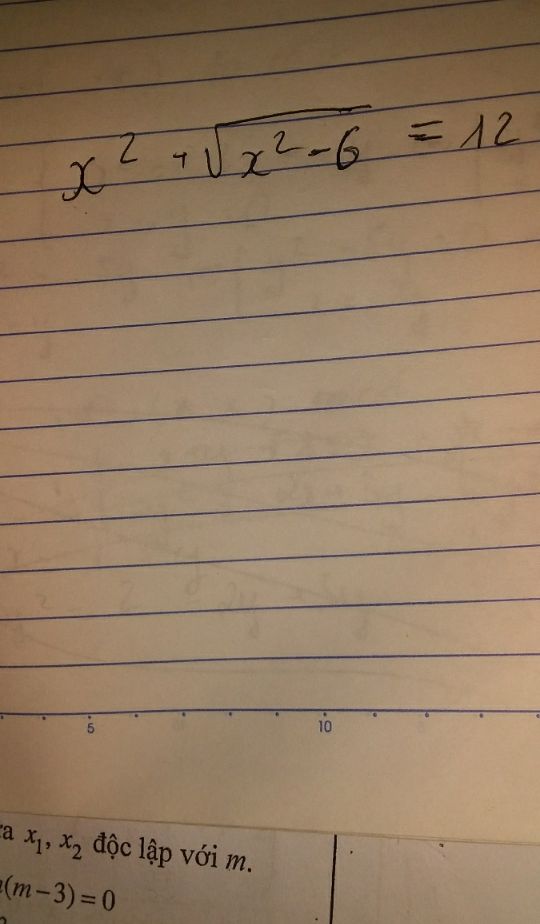 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


giải phương trình trên tập số thực:căn (x^2+x+9)= 2x-4+căn (x+1)
cảm ơn nhìu nhìu
Theo dõi (0) 0 Trả lời -


Tìm m để phương trình (x^2+mx+2)/(x^3-1)=1 vô nghiệm
bởi Lê Huy Thoại
 29/12/2019
Giải
29/12/2019
Giải Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Giải hộ mk câu 15 với
Giải hộ mk câu 15 với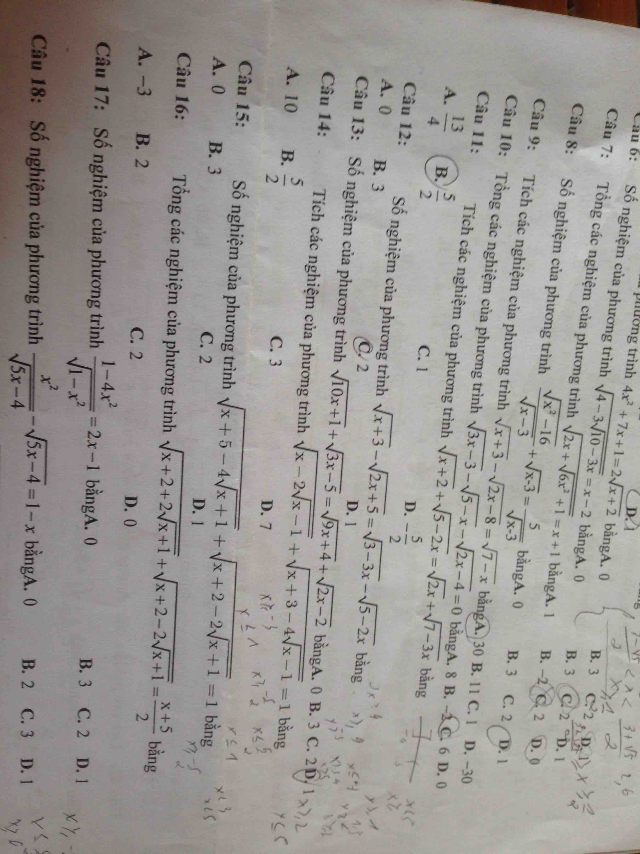 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Số các giá trị âm của tham số m để tập xác định của hàm số y=2/2m cân của (7m 1-2x) chứa đoạn [-1;1]?
bởi Phong Lê
 27/12/2019
27/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Biện luận x^2 –2(m–1)x +m–2=0
bởi Nguyễn Lee
 25/12/2019
X^2 –2(m–1)x m–2=0Theo dõi (0) 0 Trả lời
25/12/2019
X^2 –2(m–1)x m–2=0Theo dõi (0) 0 Trả lời -


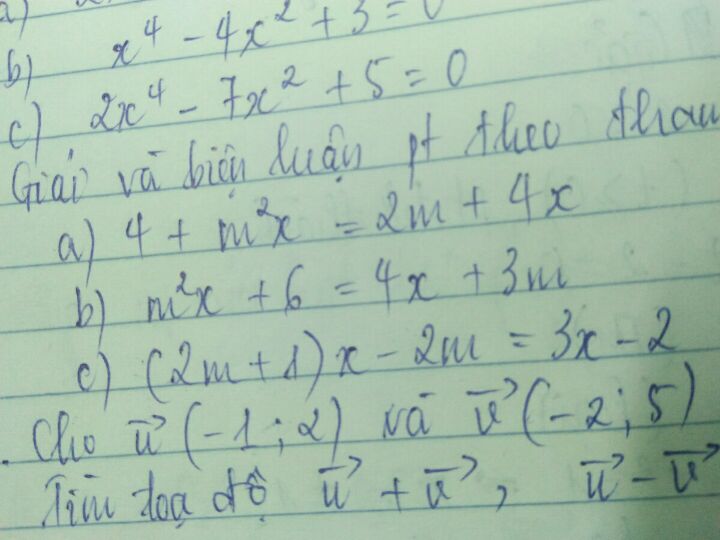 Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


Giải phương trình căn 2x+1=x-1
bởi Mai Ioc
 23/12/2019
Giải :√2× 1=×-1Theo dõi (0) 4 Trả lời
23/12/2019
Giải :√2× 1=×-1Theo dõi (0) 4 Trả lời -


Tìm tọa độ điểm D sao cho ABCD là hình bình hành
bởi Phùng Văn Hiếu
 23/12/2019
trả lời hộ e
23/12/2019
trả lời hộ e Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Mẹ sinh con lúc bao nhiêu tuổi biết hiện nay tuổi của mẹ gấp 7 lần tuổi con?
bởi Tường Vy
 23/12/2019
Hiện nay tuổi của mẹ gấp 7 lần tuổi con . Sau 2 năm nữa tuổi của mẹ gấp 5 lần tuổi con . Hỏi mẹ sinh con lúc bao nhiêu tuổiTheo dõi (0) 0 Trả lời
23/12/2019
Hiện nay tuổi của mẹ gấp 7 lần tuổi con . Sau 2 năm nữa tuổi của mẹ gấp 5 lần tuổi con . Hỏi mẹ sinh con lúc bao nhiêu tuổiTheo dõi (0) 0 Trả lời -

 Giúp e mấy câu đánh dấu ạ
Giúp e mấy câu đánh dấu ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình (x+3)căn(10-x^2)=x^2-x-12
bởi Anh Nguyễn Hoang
 21/12/2019
mong đc nhận câu trả lời sớm nhất thực sự mk đg rất cần cảm ơn ạ
21/12/2019
mong đc nhận câu trả lời sớm nhất thực sự mk đg rất cần cảm ơn ạ Theo dõi (0) 10 Trả lời
Theo dõi (0) 10 Trả lời -


Giải phương trình (x+1/x-2)^2-3(x-1/x+2)^2+2(x^2-1/x^2-4)=0
bởi vi
 20/12/2019
Giải phương trình
20/12/2019
Giải phương trình Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để phương trình m^3x=mx+m^2-m có nghiệm
bởi nanakoman
 19/12/2019
Câu 25
19/12/2019
Câu 25 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm nghiệm của phương trình x^2+5-5 căn(x^2+1)=0
bởi Duong Tran
 19/12/2019
19/12/2019
 Theo dõi (1) 6 Trả lời
Theo dõi (1) 6 Trả lời -


Giải hệ phương trình x+xy+y=2 và x^2+y^2+xy=4
bởi Việt Linh
 18/12/2019
.
18/12/2019
.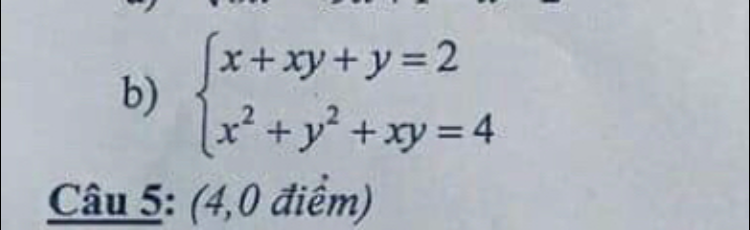 Theo dõi (2) 1 Trả lời
Theo dõi (2) 1 Trả lời -


Giải phương trình căn(x+1).(2x^2+5x+3)=0
bởi Khánh Duy
 17/12/2019
17/12/2019
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời





