Giải bài 52 tr 15 sách BT Toán lớp 9 Tập 2
Giải các hệ phương trình sau:
\(a)\left\{ {\matrix{
{\sqrt 3 x - 2\sqrt 2 y = 7} \cr
{\sqrt 2 x + 3\sqrt 3 y = - 2\sqrt 6 } \cr} } \right.\)
\(b)\left\{ {\matrix{
{\left( {\sqrt 2 + 1} \right)x - \left( {2 - \sqrt 3 } \right)y = 2} \cr
{\left( {2 + \sqrt 3 } \right)x + \left( {\sqrt 2 - 1} \right)y = 2} \cr} } \right.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Cách giải hệ phương trình bằng phương pháp cộng đại số:
+ Bước \(1\): Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.
+ Bước \(2\): Sử dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
+ Bước \(3\): Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.
Lời giải chi tiết
a)
\(\eqalign{
& \left\{ {\matrix{
{\sqrt 3 x - 2\sqrt 2 y = 7} \cr
{\sqrt 2 x + 3\sqrt 3 y = - 2\sqrt 6 } \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{\sqrt 6 x - 4y = 7\sqrt 2 } \cr
{\sqrt 6 x + 9y = - 6\sqrt 2 } \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{13y = - 13\sqrt 2 } \cr
{\sqrt 3 x - 2\sqrt 2 y = 7} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{y = - \sqrt 2 } \cr
{\sqrt 3 x - 2\sqrt 2 .\left( { - \sqrt 2 } \right) = 7} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = - \sqrt 2 } \cr
{\sqrt 3 x = 3} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{y = - \sqrt 2 } \cr
{x = \sqrt 3 } \cr} } \right. \cr} \)
Vậy hệ phương trình đã cho có một nghiệm (x; y) = \(\left( {\sqrt 3 ; - \sqrt 2 } \right)\)
b)
\(\eqalign{
& \left\{ {\matrix{
{\left( {\sqrt 2 + 1} \right)x - \left( {2 - \sqrt 3 } \right)y = 2} \cr
{\left( {2 + \sqrt 3 } \right)x + \left( {\sqrt 2 - 1} \right)y = 2} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{\left( {\sqrt 2 + 1} \right)\left( {\sqrt 2 - 1} \right)x - \left( {\sqrt 2 - 1} \right)\left( {2 - \sqrt 3 } \right)y = 2\left( {\sqrt 2 - 1} \right)} \cr
{\left( {2 + \sqrt 3 } \right)\left( {2 - \sqrt 3 } \right)x + \left( {2 - \sqrt 3 } \right)\left( {\sqrt 2 - 1} \right)y = 2\left( {2 - \sqrt 3 } \right)} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x - \left( {\sqrt 2 - 1} \right)\left( {2 - \sqrt 3 } \right)y = 2\left( {\sqrt 2 - 1} \right)} \cr
{x + \left( {2 - \sqrt 3 } \right)\left( {\sqrt 2 - 1} \right)y = 2\left( {2 - \sqrt 3 } \right)} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{2x = 2\sqrt 2 - 2 + 4 - 2\sqrt 3 } \cr
{x + \left( {2 - \sqrt 3 } \right)\left( {\sqrt 2 - 1} \right)y = 2\left( {2 - \sqrt 3 } \right)} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = \sqrt 2 + 1 - \sqrt 3 } \cr
{\left( {2 - \sqrt 3 } \right)\left( {\sqrt 2 - 1} \right)y = 4 - 2\sqrt 3 - \sqrt 2 - 1 + \sqrt 3 } \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = \sqrt 2 + 1 - \sqrt 3 } \cr
{y = {{3 - \sqrt 2 - \sqrt 3 } \over {\left( {2 - \sqrt 3 } \right)\left( {\sqrt 2 - 1} \right)}}} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = \sqrt 2 + 1 - \sqrt 3 } \cr
{y = {{\left( {3 - \sqrt 2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)\left( {\sqrt 2 + 1} \right)} \over {\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)\left( {\sqrt 2 - 1} \right)\left( {\sqrt 2 + 1} \right)}}} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = \sqrt 2 + 1 - \sqrt 3 } \cr
{y = {{\left( {3 - \sqrt 2 - \sqrt 3 } \right)\left( {2\sqrt 2 + \sqrt 6 + 2 + \sqrt 3 } \right)} \over {\left( {4 - 3} \right)\left( {2 - 1} \right)}}} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = \sqrt 2 + 1 - \sqrt 3 } \cr
{y = \sqrt 2 - 1 - \sqrt 3 } \cr} } \right. \cr} \)
Vậy hệ phương trình đã cho có một nghiệm (x; y) = \(\left( {\sqrt 2 + 1 - \sqrt 3 ;\sqrt 2 - 1 - \sqrt 3 } \right)\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 46 trang 27 SGK Toán 9 Tập 2
Bài tập 51 trang 15 SBT Toán 9 Tập 2
Bài tập 53 trang 15 SBT Toán 9 Tập 2
Bài tập 54 trang 15 SBT Toán 9 Tập 2
Bài tập 55 trang 16 SBT Toán 9 Tập 2
Bài tập 56 trang 16 SBT Toán 9 Tập 2
Bài tập 57 trang 16 SBT Toán 9 Tập 2
Bài tập III.1 trang 16 SBT Toán 9 Tập 2
Bài tập III.2 trang 16 SBT Toán 9 Tập 2
-


Một chiếc thuyền chạy qua sông với v=5km/h bị nước chảy đẩy thuyền nên thuyền di chuyển theo phương lệch 1 góc 25 độ so với phương thẳng góc với bờ
bởi lê quỳnh anh
 17/11/2019
17/11/2019
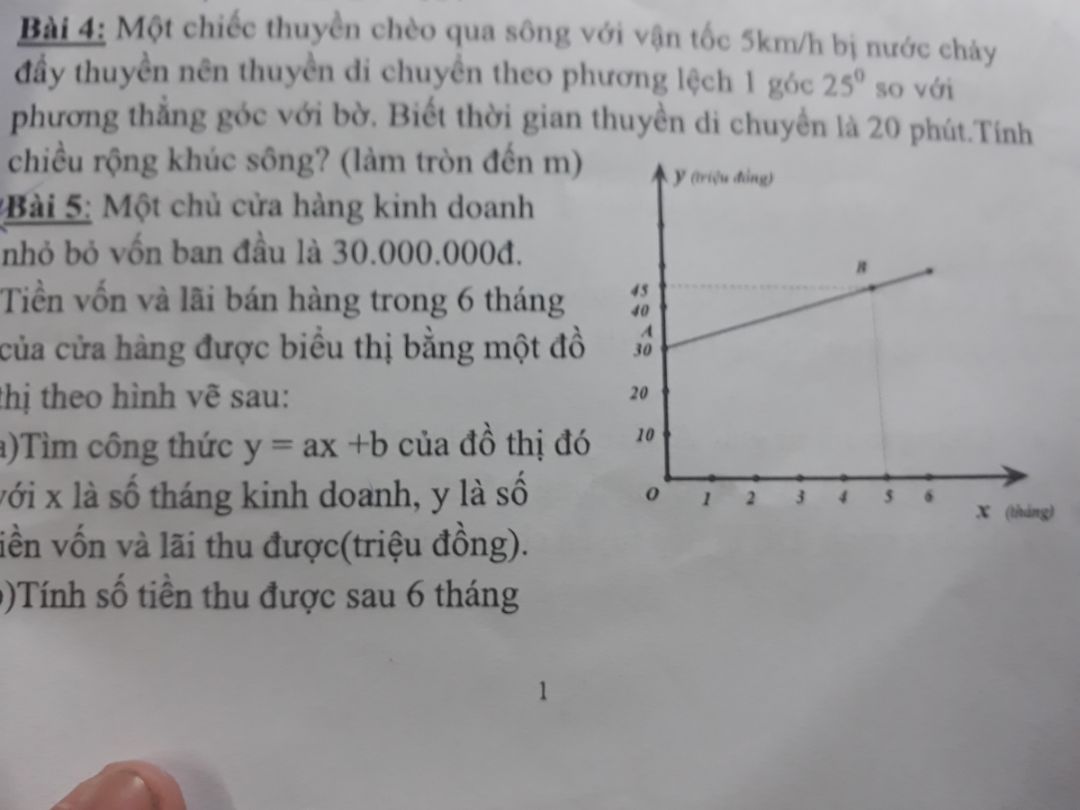 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa x^2-y^2 đạt giá trị lớn nhất
bởi Đỗ Nguyệt
 28/04/2019
28/04/2019
Cho hệ phương trình:
{x+y=3m+2
{3x-2y=11-mTìm m để hệ phương trình có nghiệm duy nhất x, y thỏa mãn x2 - y2 đạt giá trị lớn nhất
Theo dõi (0) 2 Trả lời -


Giải hệ phương trình |x+1|+|y-2|=4; 2|x+1|-|y-2|=2
bởi Ly Trúc Ly
 22/02/2019
22/02/2019
Giải hệ phương trình
{|x+1|+|y-2|=4; 2|x+1|-|y-2|=2
Theo dõi (0) 1 Trả lời -


Tìm x để thỏa mãn 1/x^2+căn x+2=x/1+căn 2x+1
bởi Quang Phan
 14/02/2019
14/02/2019
1/x^2+căn x+2=x/1+căn 2x+1
Theo dõi (0) 0 Trả lời -
ADMICRO


Lập biểu thức quãng đường từ nhà đến trường của 2 bạn theo t biết nhà Lan và Hùng đối diện nhau
bởi Võ Phạm Đoan Trang
 29/11/2018
29/11/2018
Bạn Lan đi bộ đến trường vói tốc độ trung bình 6km/h;15p sau bạn hùng đi xe đạp đến trường với tốc độ tb 16km/h Biết nhà Lan và Hùng đối diện nhau, quãng đường từ nhà đến trường là 1 đường thẳng
a.Gọi t là thời gian bạn Lan đi từ nhà đến trường.Hãy lập biểu quãng đường từ nhà đến trường của 2 bạn theo t
b.hai bạn gặp nhau cách trường bao nhiêu mét? Biết quãng đường từ nhà đến trường là 3000m
Theo dõi (0) 0 Trả lời -


Chứng minh căn(a/1-a)+căn(b/1-b)+căn(c/1-c)>2
bởi thuy tien
 28/12/2018
28/12/2018
cho các sô dương a,b,c biết a+b+c=1 chứng minh rằng
\(\sqrt{\dfrac{a}{1-a}}\)+\(\sqrt{\dfrac{b}{1-b}}\)+\(\sqrt{\dfrac{c}{1-c}}\) > 2
Theo dõi (0) 1 Trả lời -


Chứng minh rằng A = 8m^2 - 18m + 9
bởi can tu
 02/01/2019
02/01/2019
Cho PT x2 - 2mx + 2m - 1 = 0
Đặt A = 2(x12 + x22) - 5x1x2
a) Chứng minh rằng A = 8m2 - 18m + 9
b) Tìm m để đạt GTNN
Theo dõi (0) 1 Trả lời -


Chứng minh m là số nguyên tố, biết 2^m-1
bởi Đào Lê Hương Quỳnh
 02/01/2019
02/01/2019
Cho 2m-1 là một số nguyên tố.Cmr m là số nguyên tố
Theo dõi (0) 1 Trả lời -


Chứng minh 2 đồ thị luôn cắt nhau tại 2 điểm phân biệt a và b với mọi giá trị của m
bởi Mai Bảo Khánh
 02/01/2019
02/01/2019
cho prabol y=x2 và đường thẳng y=4mx-4m2+1
a)chứng minh rằng 2 đồ thị luôn cắt nhau tại 2 điểm phân biệt a và b với mọi giá trị của m
b)gọi x1;x2 là hoành độ của a và b. tính (x1-x2)2
c)tính tọa độ trung điểm y của a;b theo m
Theo dõi (0) 1 Trả lời -


Chứng minh x^2-(m-1)x-m^2-m-2=0 luôn có nghiệm trái dấu ∀m
bởi My Le
 02/01/2019
02/01/2019
Cho PT : \(x^2-\left(m-1\right)x-m^2-m-2=0\) (1)
CMR PT (1) luôn có nghiệm trái dấu \(\forall m\)
Theo dõi (0) 1 Trả lời -


1. Cho tam giác ABC vuông tại A, đường cao AH, AH = 12cm, BC = 25cm. Tính BH, HC, AB, AC
2. Tam giác ABC vuông tại B, góc A = 30 độ, AB = a. Tính độ dài các cạnh của tam giác theo a
3. Cho tam giác ABC có 3 góc nhọn
a. CM: sinA + cosA >1
b. Vẽ đường cao AH. CM: AH= BC/(cotgB+cotgC)
c. Biết BC = 12cm, góc B = 60 độ, góc C = 45độ. Tính S tam giác ABC.
4. Cho tam giác ABC có 3 góc nhọn AB=c, AC=b, BC=a.
a. Cmr: a/(sinA) = b/(sinB) = c/(sinC)
b. Biết 2a= b+c. CM: 2sinA = sinB+sinC.
5. Cho tam giác ABC có 3 góc nhọn, AB=c, AC=b, BC=a. Cmr: a^2 = (b^2)+(c^2)-2bc. cosA
6. Cho tam giác ABC có các góc đều nhọn, góc B > góc C, đường cao AH và trung tuyến AM. Đặt góc HAM = α . CM: tg α = (cotgC-cotgB)/27. Cho đường tròn tâm O và M là điểm ở ngoài đường tròn. Qua M kẻ tiếp tuyến MA, MB (A, B là tiếp điểm) và một cát tuyến cắt đường tròn tại C, D,
a/ Gọi I là trung điểm của CD. Chứng minh bốn điểm A,B,O,I nằm trên một đường tròn.
b/ AB cắt CD tại E. Chứng minh MA^2=ME.MITheo dõi (0) 1 Trả lời -


cmr: Với a, b, c > 0 chứng minh rằng 4/a + 5/b + 3/c ≥ 4(3/(a + b) + 2/(b + c) + 1/(c + a))
Theo dõi (0) 1 Trả lời -


Chứng minh (h+c)^2=(a+b)^2+h^2
bởi thu hằng
 28/12/2018
28/12/2018
Cho tam giác ABC vuông tại A ( hình vẽ ) . CMR : \(\left(h+c\right)^2=\left(a+b\right)^2+h^2\)
Mysterious Person Help me :((
Theo dõi (0) 1 Trả lời -


Cho a,b,c là các số thực khác 0 thỏa mãn a+b+c=0.CMR:
\(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}=\left|\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right|\)
Theo dõi (0) 1 Trả lời -


Chứng minh A = x^2+y^2 / x- y > 2căn2
bởi khanh nguyen
 02/01/2019
02/01/2019
cho x>y thỏa mãn xy=1. cm:
A=\(\dfrac{x^2+y^2}{x-y}\ge2\sqrt{2}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình 4 - 2t + 12 + 5t = t + 24 - 3t
bởi thu thủy
 07/01/2019
07/01/2019
giải phương trình
4 - 2t + 12 + 5t = t + 24 - 3t
Theo dõi (0) 1 Trả lời -


Chứng minh 1/p-a + 1/p-b + 1/p-c > 2(1/a+1/b+1/c)
bởi Thùy Trang
 02/01/2019
02/01/2019
cho a,b,c là độ dài ba cạnh của tam giác có chu vi 2p.cmr:
\(\dfrac{1}{p-a}+\dfrac{1}{p-b}+\dfrac{1}{p-c}\ge2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\)
Theo dõi (0) 1 Trả lời -


Chứng minh 1/a+1/b+1/c > 9/ a+b+c
bởi Nguyễn Vân
 02/01/2019
02/01/2019
cho a,b,c>0. cmr:
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{9}{a+b+c}\)
Theo dõi (0) 1 Trả lời -


Chứng minh (căn3 - căn 2) . căn(5+2 căn6) = 1
bởi Mai Vàng
 02/01/2019
02/01/2019
Bài tập: Chứng minh
a,\(\left(\sqrt{3}-\sqrt{2}\right).\sqrt{5+2\sqrt{6}}=1\)
b,\(\left[\dfrac{\sqrt{x}-\sqrt{y}}{x-y}+\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\right].\dfrac{\sqrt{xy}+1}{\sqrt{x+\sqrt{y}}}\) (với x\(\ge\) 0; y\(\ge\) 0; x\(\ne\)y)
Theo dõi (0) 2 Trả lời -


Chứng minh (ab/c+1)+(bc/a+1)+(ca/b+1)=<1/4
bởi Nguyễn Hồng Tiến
 02/01/2019
02/01/2019
Cho a, b và c là các số thực không âm thỏa mãn a + b +c = 1
CMR : \(\dfrac{ab}{c+1}\) + \(\dfrac{bc}{a+1}\) + \(\dfrac{ca}{b+1}\) \(_{\le}\) \(\dfrac{1}{4}\)
Theo dõi (0) 1 Trả lời -


\(\left\{{}\begin{matrix}\left(m+1\right)x+my=2m-1\\mx-y=m^2-2\end{matrix}\right.\)
Chứng minh rằng với mọi m hệ luôn có nghiệm duy nhất (x ; y). Tìm m sao cho P=xy+x+2y đạt giá trị lớn nhất
Theo dõi (0) 1 Trả lời -


Chứng minh A/B = x - 2/ 4 cănx
bởi A La
 02/01/2019
02/01/2019
Cho A = \(\dfrac{x-2}{2+\sqrt{x}}\) và B = \(\dfrac{4\left(2x-1\right)}{2x+1}\) với \(x>0\), x # \(\dfrac{1}{2}\), x # \(\dfrac{1}{4}\)
Chứng minh \(\dfrac{A}{B}=\dfrac{x-2}{4\sqrt{x}}\)
Theo dõi (0) 1 Trả lời -


Chứng minh (x^4/y+3z) + (y^4/z+3x) + (z^4/x+3y)>= 3/4
bởi Bo bo
 02/01/2019
02/01/2019
Cho \(xy+yz+xz\ge3\)
CMR:\(\dfrac{x^4}{y+3z}+\dfrac{y^4}{z+3x}+\dfrac{z^4}{x+3y}\ge\dfrac{3}{4}\)
Theo dõi (0) 1 Trả lời -


Chứng minh các công thức Tanα = sinα/cosα
bởi Hong Van
 02/01/2019
02/01/2019
Chứng minh các công thức sau :
\(Tan\alpha=\dfrac{sin\alpha}{cos\alpha}\)
\(Cot\alpha=\dfrac{cos\alpha}{sin\alpha}\)
\(sin^2\alpha+cos^2\alpha=1\)
\(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\)
\(1+cos^2\alpha=\dfrac{1}{sin^2\alpha}\)
\(cos^4\alpha-sin^4\alpha=2cos^2\alpha-1\)
Theo dõi (0) 1 Trả lời -


Giải phương trình x- cănx - 10 = 0
bởi thanh hằng
 07/01/2019
07/01/2019
Giải PT x -\(\sqrt{x}\)-10=0
Theo dõi (0) 1 Trả lời -


Chứng minh rằng căn ab + căn cd <= căn(a+d)(b+c)
bởi Thanh Nguyên
 02/01/2019
02/01/2019
Cho a,b,c,d >0. Chứng minh rằng:
\(\sqrt{ab}+\sqrt{cd}\le\sqrt{\left(a+d\right)\left(b+c\right)}\)
Theo dõi (0) 1 Trả lời -


a, Cho 3 số x,y,z thỏa mãn yz > 0 . CMR : x2 + yz \(\ge\) 2\(\sqrt{yz}\) Dấu = xảy ra khi nào ?
b, Cho x,y,z là 3 số dương thỏa mãn : x+y+z = 3
CMR : \(\dfrac{x}{x+\sqrt{3y+yz}}\) + \(\dfrac{y}{y+\sqrt{3y+zx}}\) + \(\dfrac{z}{z+\sqrt{3z+y}}\) \(\le\) 1
Theo dõi (0) 1 Trả lời -


Cho x, y, z \(\ge1\) và: \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=2\). C/m:
\(\sqrt{x+y+z}\ge\sqrt{x-1}+\sqrt{y-1}+\sqrt{z-1}\)
Theo dõi (0) 1 Trả lời -


Cho a + b + c = 2018
Chứng minh rằng: \(\dfrac{a^4+b^4}{a^3+b^3}+\dfrac{b^4+c^4}{b^3+c^3}+\dfrac{c^4+a^4}{c^3+a^3}\) \(\ge2018\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng a+b+c>=ab+bc+ca
bởi Trieu Tien
 02/01/2019
02/01/2019
cho a,b,c dương thỏa mãn ab+bc+ca=4. CMR: \(a+b+c\ge ab+bc+ca\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng ab+bc+ca-abc=<2
bởi Tran Chau
 02/01/2019
02/01/2019
cho a,b,c dương thỏa mãn \(a^2+b^2+c^2+abc=4\)
CMR: \(ab+bc+ca-abc\le2\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng sin^6x+cos^6=1-3sin^2x.cos^2x
bởi Nguyễn Bảo Trâm
 02/01/2019
02/01/2019
Cho 0 độ < x < 90 độ. Chứng minh rằng:
\(\sin^6x+\cos^6=1-3\sin^2x.\cos^2x\)
Theo dõi (0) 1 Trả lời





