Bài tập 39 tr 106 sách BT Toán lớp 9 Tập 2
Trên đường tròn tâm \(O\) có một cung \(AB\) và \(S\) là điểm chính giữa của cung đó. Trên dây \(AB\) lấy hai điểm \(E\) và \(H.\) Các đường thẳng \(SH\) và \(SE\) cắt đường tròn theo thứ tự tại \(C\) và \(D.\) Chứng minh \(EHCD\) là một tứ giác nội tiếp.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)
+) Nếu một tứ giác có tổng số đo hai góc đối nhau bằng \(180^\circ\) thì tứ giác đó nội tiếp được đường tròn.
Lời giải chi tiết
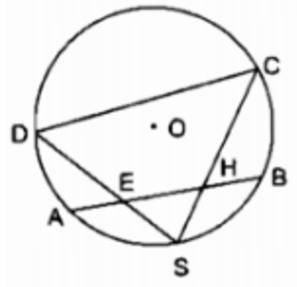
\(S\) là điểm chính giữa của cung \(\overparen{AB}\).
\( \Rightarrow \) \(\overparen{SA} = \overparen{SB}\) \((1)\)
\(\widehat {DEB} = \displaystyle {1 \over 2}(sđ \overparen{DCB} + sđ \overparen{AS})\) (góc có đỉnh ở bên trong đường tròn) \( (2)\)
\(\widehat {DCS} = \displaystyle {1 \over 2} sđ \overparen{DAS}\) (tính chất góc nội tiếp) hay \(\widehat {DCS} =\displaystyle {1 \over 2} (sđ \overparen{DA} + sđ \overparen{SA}\)) \( (3)\)
Từ \((1)\) và \((2)\) suy ra: \(\widehat {DEB} + \widehat {DCS}\)\( =\displaystyle {1 \over 2} (sđ \overparen{DCB} + sđ \overparen{AS} + sđ \overparen{DA} + sđ \overparen{SA})\) \( (4)\)
Từ \((1)\) và \((4)\) suy ra: \(\widehat {DEB} + \widehat {DCS}\)\( =\displaystyle {1 \over 2} (sđ \overparen{DCB} + sđ \overparen{BS} + sđ \overparen{SA} + sđ \overparen{DA})\) \( = \displaystyle {{360^\circ } \over 2} = 180^\circ \)
Hay \(\widehat {DEH} + \widehat {DCH} = 180^\circ \)
Vậy: tứ giác \(EHCD\) nội tiếp được trong một đường tròn.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-
Tính AC biết góc ADC=135 độ, ADC=135 độ, BD=10cm
bởi Lê Anh Tài
25/03/2019
cho tứ giác ABCD nội tiếp đường tròng tâm O đường kính BD (
0
các đường thẳng AB và CD cắt nhau tại E,các đường thẳng AD và BC cắt nhau tại F.cmr
1)BD VUÔNG VỚI EF(H là chân đường vuông góc)
2)cm BA.BE=BC.BF
3)cm D là tâm đường tròn nội tiếp tam giác AHC
4)cho
TÍNH AC
Theo dõi (1) 0 Trả lời -
cho tứ giác ABCD nội tiếp O , đường tròn đi qua ba điểm B,O,C cắt lại AB, DC theo thứ tự E và F, P là một điểm trên cung AB không chứa chung DC, PD và PC lần lượt cát AB tại K và H
a, so sánh AB.EC và AC.AE
b, chứng minh AO vuông goc với EF
c, chứng minh m=KA.HB/KH không phụ thuộc vào vị trí của điểm P
giúp mình với ạ
Theo dõi (0) 1 Trả lời -
Chứng minh tứ giác ABCD nội tiếp biết tam giác ABC nhọn có hai đường cao BE và CF
bởi Nguyễn Vũ Thành
15/02/2019
cho tam giác ABC nhọn có hai đường cao BE và CF cắt nhau tại H kẻ hình bình hành BHCD CMR tg ABCD nt
Theo dõi (0) 1 Trả lời -
cho tam giác ABC nhọn nội tiếp đường tròn (O;R) có BC=R√3 và AB<AC. gọi H là trực tâm tam giác ABC nối AH cắt đường tròn tại điểm D khác A.
a,tính góc BAC. suy ra tam giác OAH cân
b, CMR AD*BC=AB*CD+AC*BD
Theo dõi (0) 1 Trả lời -
ADMICRO
Cho tam giác ABC ( AB>AC) có 3 góc nhọn nội tiếp đường tròn tâm O . Các đg cao BD;CE;AK cắt nhau tại H . Kẻ đg kính AM;AH cắt (O) tại N.
a)Cm: Tứ giác BHCM là hình bình hành
b)Cm: Tam giác ABK đồng dạng với tam giác ACM, từ đó so sánh BN với CM
c)Cm: tam giác BHN cân và tứ giác BNMC là hình thang cân
mình cảm ơn ạ !
Theo dõi (0) 0 Trả lời -
Chứng minh tam giác ADE và ABC đồng dạng biết tam giác ABC nhọn nội tiếp (O)
bởi Đào Mai Phương
03/02/2019
Cho tam giác nhọn ABC nội tiếp đường tròn tâm (O;R) có cạnh BC cố định còn điểm A thay đổi trên đường tròn (O). Các đường cao BD, CE của tam giác ABC cắt nhau tại H. Tia ED cắt (O) tại M.
a, Chứng minh tam giác ADE và ABC đồng dạng
b, Chứng minh AO vuông góc với DE
c, Chứng minh : AM^2 = AD. AC
d, Chứng minh AH không đổi khi A thay đổi trên (O)
Theo dõi (0) 0 Trả lời -
Cho tam giác ABC nội tiếp đường tròn (O), hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF.
a) Tứ giác BFCH là hình gì?
b) Gọi M là trung điểm của BC. CMR: 3 điểm H,M,F thẳng hàng
c) CMR: OM=1/2AH
Theo dõi (0) 0 Trả lời -
Chứng minh 4 điểm M, A, B, O cùng thuộc một đường tròn biết MA, MB là 2 tiếp tuyến của đường tròn (O)
bởi Monsloc Relo
27/12/2018
Cho đường tròn O là một điểm M nằm ngoài đường tròn. Từ M kẻ hai tiếp tuyến MA, MB với đường tròn O (A và B là hai tiếp điểm ) Gọi I là giao điểm của OM và AB
a) Chứng minh 4 điểm M, A, B, O cùng thuộc một đường tròn
b) chm: OM vuông góc với AB tại I
c) Từ B kẻ đường kính BC của đường tròn O đường kính MC cắt đường tròn O tại D (D khác C)
d) Qua O vẽ đường thẳng vuông góc với MC tại E và cắt đường thẳng BA tại F chứng minh FC là tiếp tuyến của đường tròn O
Theo dõi (1) 5 Trả lời -
Chứng minh 4 điểm B, E, F, I cùng thuộc 1 đường tròn biết cung CD vuông góc với AB tại I
bởi Trần Ngọc Tuân
27/11/2018
Cho đường tròn tâm ( O) đường kính AB. Về cung CD vuông góc với AB tại I( I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC, CE khác B và C, AE cắt CD tại F. Cm 4 điểm B, E, F, I cùng thuộc 1 đường tròn
Theo dõi (1) 3 Trả lời -
câu 1: nếu hai đường tròn (o) và (o') có bán kính lần lượt là R=5cm và r= 3cm và khoảng cách hai tâm là 7cm thì (o) và (o').
A. tiếp xúc ngoài B. cắt nhau tại hai điểm
c. không có điểm chung D. tiếp xúc trong
câu 2: cho hình vuông MNPQ có cạnh bằng 4cm. bán kính đường tròn ngoại tiếp hình vuông đó bằng:
A. 2cm B.
cm
C.
cm D.
cm
câu 3: khoanh tròn trước câu trả lời sai.
cho
,
. khi đó:
A.
B.
C.
D.
Theo dõi (1) 6 Trả lời -
Chứng minh B, I, K, C thuộc đường tròn tâm O biết tam giác ABC có M là trung điểm của BC
bởi Lan Hikari
31/10/2018
Cho tam giác ABC có M là trung điểm của BC, MD vuông góc AB, ME vuông góc AC. Trên tia BD và CE lấy I và K sao cho D là trung điểm của BI, E là trung điểm của CK.
a, C/m 4 điểm B,I,K,C thuộc đường tròn tâm O.
b, BIC là tam giác gì?
< Các bạn giải hộ mình bài này với, mình đang cần gấp. Thanks nhiều ạ >Theo dõi (0) 3 Trả lời
