Giải bài 60 tr 90 sách GK Toán 9 Tập 2
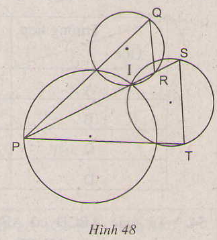
Xem hình 48. Chứng minh QR // ST.
Hướng dẫn giải chi tiết bài 60
Với bài 60 này, chúng ta sẽ vẽ lại hình, rồi sử dụng tính chất góc ngoài của tứ giác nội tiếp để giải quyết bài toán
.png)
Ta có tứ giác ISTM nội tiếp đường tròn nên theo tính chất góc ngoài của tứ giác, ta có:
\(\small \widehat{PST}=\widehat{IMP}\)
Mặc khác, tứ giác PMIN cũng là tứ giác nội tiếp, theo tính chất góc ngoài, ta có:
\(\small \widehat{IMP}=\widehat{INQ}\)
Lại sử dụng tính chất góc ngoài đối với tứ giác QSIN nội tiếp trong một đường tròn:
\(\small \widehat{INQ}=\widehat{QST}\)
Từ các điều trên, ta có thể suy ra:
\(\small \widehat{PST}=\widehat{QST}\)
Mà hai góc này ở vị trí so le trong nên ta có điều cần chứng minh:
\(\small ST//QR\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 58 trang 90 SGK Toán 9 Tập 2
Bài tập 59 trang 90 SGK Toán 9 Tập 2
Bài tập 39 trang 106 SBT Toán 9 Tập 2
Bài tập 40 trang 106 SBT Toán 9 Tập 2
Bài tập 41 trang 106 SBT Toán 9 Tập 2
Bài tập 42 trang 107 SBT Toán 9 Tập 2
Bài tập 43 trang 107 SBT Toán 9 Tập 2
-


Chứng minh tứ giác nội tiếp
bởi TC Dũng
 07/02/2020
Các bạn hướng mình cách giải câu 6.d) được không ạ? Tks
07/02/2020
Các bạn hướng mình cách giải câu 6.d) được không ạ? Tks Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh ABCM là tứ giác nội tiếp biết tam giác ABC vuông tại A, AC=3AB
bởi Vương Đình Hiển
 29/01/2020
Giúp mình với mn ơiTheo dõi (0) 1 Trả lời
29/01/2020
Giúp mình với mn ơiTheo dõi (0) 1 Trả lời -


ho đường tròn (O;R) và dây cung BC không đi qua tâm. Gọi A là điểm chính giữa của cung nhỏ BC. Góc nội tiếp quay quanh điểm A và có số đo không đổi sao cho E,F khác phía với điểm A so với BC;AF và AE cắt đường thẳng BC lần lượt tại M và N. Lấy điểm D sao cho tứ giác MNED là hình bình hành. a. Chứng minh MNEF là tứ giác nội tiếp.
bởi vi vi
 12/01/2020
12/01/2020
Cho đường tròn (O;R) và dây cung BC không đi qua tâm. Gọi A là điểm chính giữa của cung nhỏ BC. Góc nội tiếp quay quanh điểm A và có số đo không đổi sao cho E,F khác phía với điểm A so với BC;AF và AE cắt đường thẳng BC lần lượt tại M và N. Lấy điểm D sao cho tứ giác MNED là hình bình hành.
a. Chứng minh MNEF là tứ giác nội tiếp. b. Gọi I là tâm đường tròn ngoại tiếp tam giác MDF. Chứng minh rằng khi góc nội tiếp EAF quay quanh điểm A thì I chuyển động trên một đường thẳng cố định. c. Khi EAF= 60và BC=R, tính theo R độ dài nhỏ nhất của đoạn OI
Theo dõi (0) 0 Trả lời -


Chứng minh tứ giác BCEF nội tiếp biết tam giác ABC nhọn nội tiếp đường tròn (O) có đường cao AD
bởi Hoàng Thị Hương Giang
 18/05/2019
18/05/2019
Cho tam giác nhọn ABC (AB<AC) nột tiếp đường tròn (O) có đường cao AD.Vẽ DE vuông góc với AC tại E và DF vuông góc với AB tại F:
a/Chứng minh góc AFE = góc ADE và tứ giác BCEF nội tiếp .
b/Tia È cắt tia CB tại M , đoạn thẳng AM cắt đường tròn (O) tại N (khác A).Chúng minh : MN.MA=MF.ME
c/Tia ND cắt đường tròn (O) tại I . Chứng minh OI vuông góc với EF.
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh tứ giác DEMK nội tiếp biết đường kính CD vuông góc với AB tại K
bởi White Selena
 30/04/2019
30/04/2019
Cho đường tròn tâm O và dây AB. Vẽ đường kính CD vuông góc với AB tại K (D thuộc cung nhỏ AB). M là một điểm thuộc cung nhỏ BC sao cho cung MC < cung MB. DM cắt AB tại F. Tia CM cắt đường thẳng AB tại E
a) Chứng minh tứ giác DEMK nội tiếp
b) Chứng minh KE.KF=KD.KC
c) Tiếp tuyến tại M của (O) cắt AE ở I. Chứng minh IE=IF
d) Chứng minh FB.EK=EB.KA (chưa làm được)Theo dõi (1) 2 Trả lời -


Cho nửa đường tròn( O;R) đường kính AB
bởi Vũ Sông Hương
 25/04/2019
25/04/2019
Cho nửa đường tròn( O;R) đường kính AB. Trên nửa mp bờ là đường thẳng AB chứa nửa đường tròn, kẻ Ax ⊥ AB trên đó lấy điểm C ( C ≠ A). Kẻ tiếp tuyến CM tới đường tròn ( M là tt). Qua O kẻ đường thẳng ⊥ OC cắt CM tại D.
1. CMR: tứ giác AOMC nội tiếp
2. BD là tiếp tuyến của đường tròn ( O )
3. OC giao MA tại E; OD giao MB tại F; kẻ MH vuông góc với AB.
Chứng minh: HE2 + HF2có gtrị không đổi khi C chuyển đường trên tia Ax.
4. CM: 3 đường thẳng BC;EF và MH đồng quy.
Theo dõi (1) 1 Trả lời -


Từ điểm A nằm ngoài đường tròn (O; R), vẽ 2 tiếp tuyến AB và AC của đường tròn. Chứng minh tứ giác ABOC nội tiếp được
Theo dõi (0) 5 Trả lời -


Chứng minh tứ giác BFEC và AFHE nội tiếp biết 3 đường cao AD, BE và CF cắt nhau tại H
bởi Nguyễn Ngọc Hiền
 18/04/2019
18/04/2019
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O ; R ) ba đường cao AD , BE và CF cắt nhau tại H .
a) Chứng minh các tứ giác BFEC và AFHE nội tiếp .
b) Chứng minh DA là tia phân giác của góc EDF .
c) AO cắt (O) tại K . Chứng minh tứ giác BHCK là hình bình hành .
d) G là trọng tâm tam giác ABC . Chứng minh diện tích tam giác AHG bằng hai lần diện tích tam giác AOG.
Theo dõi (1) 1 Trả lời -


bài tập: Từ một điểm A ở bên ngoài đường tròn (O;R), vẽ hai tiếp tuyến AB, AC (B, C là hai tiếp điểm), và cát tuyến AMN. Gọi I là trung điểm của dây MN.
a) Chứng minh 5 điểm A, B, I, O, C cùng nằm trên một đường tròn.
b) Nếu AB = OB thì tứ giác ABOC là hình gì? Vì sao?
c) Cho AB = R. Tính diện tích hình tròn và độ dài đường tròn ngoại tiếp tứ giác ABOC theo R
ai biết chỉ giúp mình với mình đang cần gaaaaapsppppp lắm.Theo dõi (2) 0 Trả lời -


Cho tam giác DEF nhọn (DE<DF) nội tiếp đường tròn tâm O đường kính DK, tia tiếp tuyến tại K cắt tia EF ở H. Tia OH cắt DF tại G; I là trung điểm của EF.
a, Chứng minh tứ giác OIKH nội tiếp
b, Chứng minh tam giác ODG đồng dạng với tam giác IEK
Theo dõi (0) 0 Trả lời -


Chứng minh CE.CB=CK.CA biết tam giác ABC có 3 góc nhọn nội tiếp đường tròn C tâm O
bởi Tiếu Mục Hàn
 31/03/2019
31/03/2019
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn C tâm O bán kính R. Hai đường cao AE và BK của tam giác ABC cắt nhau tại H ( với E thuộc BC, K thuộc AC)
1. Chứng minh tg AEBK nội tiếp đường tròn
2. Chứng minh CE.CB=CK.CA
3. Chứng minh góc OCA = góc BAEcho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB,AC lần lượt tại các điểm M,N . Gọi H là gia điểm BN, CM; P là giao điểm AH và BC
1. Chứng minh tứ giác AMHN nội tiếp đường tròn
2. Chứng minh BM.BA=BP.BC
3. Trong trường hợp đặc biệt khi tam giác ABC đều cạnh bằng 2a. Tính chu vi đường tròn ngoại tiếp tứ giác AMHN theo a
4. Từ A kẻ các tiếp tuyển AE và AF của đường tròn tâm O đường kính BC ( E,F là các tiếp điểm). Chứng minh ba điểm E,H,F thằng hàngTheo dõi (0) 0 Trả lời





