Bài tập 41 tr 106 sách BT Toán lớp 9 Tập 2
Cho tam giác cân \(ABC\) có đáy \(BC\) và \(\widehat A = {20^0}\). Trên nửa mặt phẳng bờ \(AB\) không chứa điểm \(C\) lấy điểm \(D\) sao cho \(DA = DB\) và \(\widehat {DAB} = {40^0}\). Gọi \(E\) là giao điểm của \(AB\) và \(CD.\)
\(a)\) Chứng minh \(ACBD\) là tứ giác nội tiếp
\(b)\) Tính \(\widehat {AED}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong tam giác cân, hai góc ở đáy bằng nhau.
+) Nếu một tứ giác có tổng số đo hai góc đối nhau bằng \(180^\circ\) thì tứ giác đó nội tiếp được đường tròn.
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Lời giải chi tiết
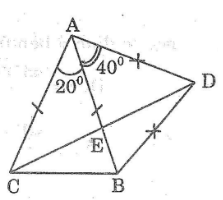
\(a)\) \(∆ABC\) cân tại \(A \;\;(gt).\)
\( \Rightarrow \widehat {ACB} = \widehat {ABC}\) (tính chất tam giác cân)
\( \Rightarrow \widehat {ACB} =\displaystyle {{180^\circ - \widehat A} \over 2} \)\(= \displaystyle {{180^\circ - 20^\circ } \over 2} = 80^\circ \)
\(∆DAB\) cân tại \(D\) (do \(DA=DB)\)
\( \Rightarrow \widehat {DBA} = \widehat {DAB}\) (tính chất tam giác cân) mà \(\widehat {DAB} = 40^\circ \) (gt) \( \Rightarrow \widehat {DBA} = 40^\circ \)
\(\widehat {ADB} = 180^\circ - (\widehat {DAB} + \widehat {DBA})\)\( = 180^\circ - (40^\circ + 40^\circ ) = 100^\circ \)
Trong tứ giác \(ACBD\) ta có: \(\widehat {ACB} + \widehat {ADB} \)\(= 80^\circ + 100^\circ = 180^\circ \)
Vậy: Tứ giác \(ACBD\) nội tiếp.
\(b)\) Vì tứ giác \(ACBD\) nội tiếp (câu a) nên xét đường tròn ngoại tiếp tứ giác \(ACBD\) ta có:
+) \(\widehat {BAC} =\displaystyle {1 \over 2} sđ \overparen{BC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{BC}\)\( = 2\widehat {BAC} = 2.20^\circ = 40^\circ \)
+) \(\widehat {DBA} =\displaystyle {1 \over 2}sđ \overparen{AD}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{AD}\) \( = 2\widehat {DBA} = 2.40^\circ = 80^\circ \)
+) \(\widehat {AED}\) là góc có đỉnh ở trong đường tròn ngoại tiếp tứ giác \(ACBD\)
\(\widehat {AED} =\displaystyle {1 \over 2}(sđ \overparen{BC} + sđ \overparen{AD})\) \( = \displaystyle {{40^\circ + 80^\circ } \over 2} = 60^\circ \)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Chứng minh được AD⊥BC và AH*AD= AE * AC
bởi Đào Thị Nhàn
 24/01/2019
24/01/2019
Cho AB < AC , đường tròn tâm O đường kính BC cắt AC , AB tại E và F . H là giao BE và CF . D là giao cảu AH và BC :
a) Chứng minh được AD\(\perp\)BC và AH*AD= AE * AC
b) Chứng minh giúp mình : tứ giác EFDO nội tiếp .
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác MCED nội tiếp
bởi Bo bo
 24/01/2019
24/01/2019
giúp mình vẽ hình cái:
cho đường tròn tâm O bán kính r đường kính AB , lấy hai điểm ME theo thứ tự AMEB trên đường tròn . Gọi C bằng AM giao với BE và D bằng AE giao với BM .
a, chứng minh tứ giác MCED nội tiếp
b, H bằng AB giao CD . chứng minh BE.BC=BH.BA
c,chứng minh các tiếp tuyến tại M và E của đường tròn O cắt nhau tại một điểm nằm trên đường thẳng CD
giúp mình giải luôn hì
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh AMHN nội tiếp, đường cao AI, BN cắt nhau tại H, CH cắt AB tại M
bởi Nguyễn Minh Hải
 24/01/2019
24/01/2019
Cho ΔABC nội tiếp (O) đường cao AI, BN cắt nhau tại H . CH cắt AB tại M .
a, CM : AMHN nội tiếp
b, Điểm H cách đều các đường thẳng MN và NI
c, CM : MN = BC . cos góc BAC biết góc BAC = 45 độ Diện tích Δ ABC = 100 cm2 Tính diện tích ΔANMTheo dõi (0) 1 Trả lời -


Chứng minh rằng tứ giác AECD nội tiếp
bởi Thùy Trang
 25/01/2019
25/01/2019
Từ 1 điểm M nằm ngoài (O) kẻ hai tiếp tuyến MA và MB với đường tròn. Trên cung nhỏ AB lấy C và kẻ CD\(\perp\)AB, CE\(\perp\)MA, CF\(\perp\)MB. Gọi I và K là giao điểm của AC với DE và của BC với DF.
a, C/m tứ giác AECD nội tiếp
b, C/m: \(CD^2=CE.CF\)
c, C/m Tia đối của tia CD là phân giác của \(\widehat{FCE}\)
d, C/m IK//AB
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh rằng OAMC nội tiếp
bởi A La
 25/01/2019
25/01/2019
Cho đường tròn (O) Từ M nằm ngoài đường tròn (O) kẻ tiếp tuyến MA,MB, cát tuyến MBD . OM cắt AC tại H .Từ C kẻ đường thẳng song song với BD cắt đường tròn (O) tại E. AE cắt BD tại K.
Chứng minh rằng:
a) OAMC nội tiếp
b) K là trung điểm BD
c) Ac là phân giác ∠BHD
XIN GÍUP EM VỚI Ạ!
Theo dõi (0) 1 Trả lời -


Chứng minh IA/ID = AM . AN/AB^2
bởi Lê Minh Bảo Bảo
 25/01/2019
25/01/2019
Cho (O) đường kính AB đừơng thẳng d tiếp xúc (O) tại A . Gọi M,N là 2 điểm trên d sao cho A nằm giữa M,N . Các đường thẳng BM,BN cắt (O) tại D,E (\(\ne\)BC). a)Chứng minh DEMN là tứ giác nội tiếp
b) Chứng minh \(\dfrac{IA}{ID}=\dfrac{AM.AN}{AB^2}\)(với I là giao điểm AB và DE)
c)Khi M,N thay đổi trên d nằm về 2 phía của A thỏa mãn AM.AN là 1 đai lượng không đổi . Chứng minh DE luôn đi qua 1 điểm cố định
Theo dõi (0) 1 Trả lời -


Chứng minh APMQ là tứ giác nội tiếp và xác định tâm O của đường tròn ngoại tiếp tứ giác
bởi Thu Hang
 25/01/2019
25/01/2019
Cho tam giác đều ABC có đường cao AH,lấy điểm M tuỳ ý thuộc HC(M không trùng với H,C).Hình chiếu vuông góc của M lên AB,AC tại P,Q.a,C/m:APMQ là tứ giác nội tiếp và xác định tâm O của đường tròn ngoại tiếp tứ giác APMQ;b,CMR:BP.BA=BH.BM;c,CMR:khiM thay đổi trên HC thì MP+MQ không đổi
Theo dõi (0) 1 Trả lời -


Chứng minh góc CND=góc CAD và tam giác MAD vuông
bởi Tran Chau
 25/01/2019
25/01/2019
Cho (O) đường kính AB,trên tia AB lấy điểm C bên ngoài đường tròn.Từ C kẻ CD vuông góc với AC và CD=AC.Nối AD cắt đường tròn(O) tại M.Kẻ BD cắt đường tròn(O) tại N.a,C/m:ANCD là tứ giác nội tiếp.Xác địmh đường kính và tâm của đường tròn ngoại tiếp tứ giác ANCD;b,C/m:góc CND=góc CAD và tam giác MAD vuông cân;c,C/m:AB.AC=AM.AD
Theo dõi (0) 1 Trả lời -


Chứng minh rằng tứ giác BCDE nội tiếp
bởi Tra xanh
 25/01/2019
25/01/2019
Bài 4 Cho nửa đường tròn đường kính AB và dây AC. Từ một điểm D trên AC, vẽ DE vuông góc với AB. Hai đường thẳng DE và BC cắt nhau tại F. Chứng minh rằng:
a) Tứ giác BCDE nội tiếp.
b)góc AFE= ACE.
Bài 5. Cho nứa đường tròn đường kính AB. Lấy hai điểm C và D trên nửa đường tròn sao cho cung AC= cung CD= cung DB. Các tiếp tuyến vẽ từ B và C của nửa đường tròn cắt nhau tại I.Hai tia AC và BD cắt nhau tại K. Chứng minh rằng:
a) Các tam giác KAB và IBC là những tam giác đêu.
b) Tứ giác KIBC nội tiếp.
Bài 6. Cho nửa đường tròn (0) đường kính AB và tia tiếp tuyến Bx của nửa đường tròn. Trên tia Bx lấy hai điểm C và D (C nằm giữa B và D). Các tia AC và BD lần lượt cắt đường tròn tại E và F. Hai dây AE và BF cắt nhau tại M. Hai tia AF và BE cắt nhau tại N. Chứng minh rằng:
a) Tứ giác FNEM nội tiêp.
b) Tứ giác CDFE nội tiếp.
Bài 7. Cho tam giác ABC. Hai đường cao BE và CF cắt nhau tại H. Gọi D là điểm đối xứng của H qua trung điểm M của BC. a) Chứng minh rằng tứ giác ABDC nội tiếp được đường tròn. Xác định tâm 0 của đường tròn đó
b) Đường thẳng DH cắt đường tròn (0) tại điểm thứ hai là I. Chứng minh rằng năm điểm A, I, F, H, E cùng nằm trên một đường tròn
Các bạn giải giúp mình các bài này nhé, mình cảm ơn nhiều lắm
Theo dõi (0) 1 Trả lời -


Chứng minh MHOI, NKOI là tứ giác nội tiếp
bởi minh vương
 25/01/2019
25/01/2019
Cho đường tròn tâm O và dây AB. I là trung điểm của AB qua I kẻ 2 dây CD và EF, CF, DE cắt AB tại M,N. Gọi H,K là trung điểm của CF,DE.
Chứng minh : a) MHOI, NKOI là tứ giác nội tiếp
b) Tam giác FHI đồng dạng tam giác DKI
c) I là trung điểm của MN
Theo dõi (0) 1 Trả lời -


Chứng mình tứ giác AEKC nội tiếp đường tròn
bởi Bo bo
 25/01/2019
25/01/2019
Cho tam giác ABC cân tại A nôi tiếp đường tròn tâm O, đường kính AI. Gọi E là trung điểm của AB, K là trung điểm của OI. Chứng mình tứ giác AEKC nội tiếp đường tròn.
Theo dõi (0) 1 Trả lời





