Bài tập 43 tr 107 sách BT Toán lớp 9 Tập 2
Cho hai đoạn thẳng \(AC\) và \(BD\) cắt nhau tại \(E.\) Biết \(AE.EC = BE.ED\). Chứng minh bốn điểm \(A, B, C, D \)cùng nằm trên một đường tròn.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Các điểm cùng nhìn một cạnh cố định dưới góc bằng nhau thì các điểm đó cùng thuộc một cung chứa góc vẽ trên cạnh cố định.
+) Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn.
Lời giải chi tiết
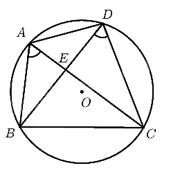
Từ \(AE. EC =BE. ED \;\;(gt)\)
\( \Rightarrow \displaystyle {{AE} \over {ED}} = {{BE} \over {EC}}\)
Xét \(∆AEB\) và \(∆DEC:\)
\(\displaystyle {{AE} \over {ED}} = {{BE} \over {EC}}\)
\(\widehat {AEB} = \widehat {DEC}\) (đối đỉnh)
Suy ra: \(∆AEB\) đồng dạng \(∆DEC\;\; (c.g.c)\)
\( \Rightarrow \widehat {BAE} = \widehat {CDE}\) hay \(\widehat {BAC} = \widehat {CDB}\)
Từ đó: \(A\) và \(D\) nhìn đoạn \(BC\) cố định dưới một góc bằng nhau nên \(4\) điểm \(A,B, C, D\) nằm trên một đường tròn.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Chứng minh BEFI nội tiếp
bởi Nguyễn Phương Khanh
 29/01/2019
29/01/2019
Cho (O) đkính AB.Vẽ dây CD vuông với AB tại I (I nằm giữa A và O).Lấy E thuộc cung BC nhỏ (E khác B,C) AE cắt CD tại F
a)Chứng minh BEFI nội tiếp
b) AE×AF=AC^2
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, góc A bằng 90 độ, AH vuông BC, Biết \(\dfrac{AB}{AC}=\dfrac{1}{\sqrt{3}},HC-HB=8\)
a) tính các cạnh của tam giác ABC ?
b) Hình chữ nhật MNIQ nội tiếp tam giác ABC (I,Q thuộc BC ; M thuộc AB ; N thuộc AC). Tìm giá trị lớn nhất của \(S_{MINQ}?\)
Theo dõi (0) 1 Trả lời -


Chứng minh AMHN là tứ giác nội tiếp
bởi Bánh Mì
 30/01/2019
30/01/2019
Cho tam giác ABC không có góc tù. Đg cao AH và đg tr tuyến AM kh trùng nhau. Gọi N là tr điểm AB. Cho biết góc BAH = góc CAM
a. Cm AMHN là tứ giác nội tiếp
b. Tính sđ góc BAC
Theo dõi (0) 1 Trả lời -


Chứng minh AHCK là tứ giác nội tiếp đường tròn
bởi Thùy Nguyễn
 12/02/2019
12/02/2019
cho tam giác nhọn ABC nội tiếp đường tròn (O) và AB<AC. Gọi H là trực tâm của tam giác ABC , AH giao đường tròn O tại L . Lấy F bất kì trên cung LC nhỏ ( F khác L và C). AC là đường trung trực của FK
1. CMR:AHCK là tứ giác nội tiếp đường tròn
2.HK giao AC tại I, À giao HC tại G. chứng minh AO vuông góc với GITheo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh tứ giác OCMD nội tiếp
bởi Mai Rừng
 13/02/2019
13/02/2019
Vẽ hình bài giúp mk với
trên đường tròn (O;R) cho trước , vẽ dây cung AB cố định không đi qua O. điểm M bất kì trên tia BA sao cho M nằm ngoài đường tron (O;R). từ M kẻ hai tiếp tuyến MC và MD với đường tròn (O;R) (C,D là hai tiếp điểm)
a, c/m tứ giác OCMD nội tiếp
B, chứng minh \(MC^2\)=MA.MB
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác ABHD nội tiếp (O)
bởi Nguyễn Quang Thanh Tú
 13/02/2019
13/02/2019
-cho \(\Delta\)ABC vuông ở A có AH là đường cao và BE là đường phân giác ( H thuộc BC, E thuộc AC) .kẻ AD\(\perp\)BE tại D
a)CMR: tứ giác ABHD nội tiếp (O)
b)CMR:\(\widehat{HDC}=\widehat{CEH}\)
Theo dõi (0) 1 Trả lời -


Chứng minh MF=1/2BC biết tam giác ABC nhọn có BE vuông góc AC, CF vuông góc AB
bởi Thu Hang
 26/04/2019
26/04/2019
Cho tam giác nhọn ABC. Kẻ BE vuông góc với AC, CF vuông góc với AB. ( E thuộc AC, F thuộc AB).
a) Gọi M là trung điểm của BC. Chứng minh rằng: MF= 1/2 BC và tam giác MEF cân
b) chứng minh rằng: góc CBF + góc CEF= 180 độ
c) Chứng minh góc BEF bằng góc BCF
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AEM đồng dạng tam giác CAM
bởi Nguyễn Thị Thúy
 21/02/2019
21/02/2019
Cho đường tròn tâm O đường kính R dây AB= R . M N lần lược thuộc điểm chính giữa cung nhỏ và lớn AB. Trên cung nhỏ AN lấy C , trên cung nhỏ BN lấy D MC cắt AB tại E . MD cắt AB tại F
a)Chứng minh tam giác AEM đồng dạng tam giác CAM
b)Chứng minh tứ giác CEFD nội tiếp
Theo dõi (0) 1 Trả lời -


Bài 7.1 trang 107 sách bài tập toán 9 tập 2
bởi Nguyễn Thanh Trà
 09/10/2018
09/10/2018
Bài 7.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 107)
Cho tam giác ABC có 3 góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy. Gọi H là giao điểm của các đường cao vừa vẽ
a) Chỉ ra các tứ giác nội tiếp có đỉnh lấy trong số các điểm A, B, C, H, I, K, L
b) Chứng minh \(\widehat{LBH},\widehat{LIH},\widehat{KIH},\widehat{KCH}\) là bốn góc bằng nhau
Theo dõi (0) 1 Trả lời -


Bài 43 trang 107 sách bài tập toán 9 tập 2
bởi Nguyễn Anh Hưng
 09/10/2018
09/10/2018
Bài 43 (Sách bài tập - tập 2 - trang 107)
Cho hai đoạn thắng AC và BD cắt nhau tại E. Biết AE.EC = BE.ED.
Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn ?
Theo dõi (0) 1 Trả lời -


Bài 42 trang 107 sách bài tập toán 9 tập 2
bởi thu hằng
 09/10/2018
09/10/2018
Bài 42 (Sách bài tập - tập 2 - trang 107)
Cho ba đường tròn cùng đi qua một điểm P. Gọi các giao điểm khác P của hai trong ba đường tròn đó là A, B, C. Từ một điểm D (khác điểm P) trên đường tròn (PBC) kẻ các tia DB, DC cắt các đường tròn (PAB) và (PAC) lần lượt tại M và N. Chứng minh ba điểm M, A, N thẳng hàng ?
Theo dõi (0) 1 Trả lời





