Giải bài 3 tr 67 sách GK Toán 8 Tập 1
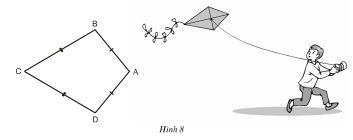
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều"
a) Chứng minh rằng AC là đường trung trực của BD.
b) Tính \(\widehat{B}, \widehat{D}\) biết rằng \(\widehat{A}= 100^0\) và \(\widehat{C}= 60^0\) .
Hướng dẫn giải chi tiết
Câu a:
Ta có: AB = AD (gt) ⇒ A thuộc đường trung trực của BD
CB = CD (gt) ⇒ C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
Câu b:

Xét \(∆ ABC\) và \(∆ADC\) có:
+) \(AB = AD\) (giả thiết)
+) \(BC = DC\) (giả thiết)
+) \(AC\) cạnh chung
Suy ra \(∆ ABC = ∆ADC\) (c.c.c)
\(\Rightarrow \widehat B = \widehat D\) (hai góc tương ứng)
Xét tứ giác \(ABCD\), ta có: \(\widehat B + \widehat {BC{\rm{D}}} + \widehat {\rm{D}} + \widehat {BA{\rm{D}}} = {360^0}\) (Định lí tổng các góc của một tứ giác).
\(\begin{array}{l}
\Rightarrow \widehat B + \widehat {\rm{D}} = {360^0} - \left( {\widehat {BC{\rm{D}}} + \widehat {BA{\rm{D}}}} \right) \\\;\;\;\;\;\;\;\;\;\;\;= {360^0} - \left( {{{60}^0} + {{100}^0}} \right) = {200^0}\\ \text{Mà }\widehat B= \widehat D\text{ (chứng minh trên) }\\
\Rightarrow \widehat B+\widehat B = {200^0}\\\Rightarrow 2\widehat B = 200^0
\end{array}\)
Do đó \(\widehat B = \widehat {\rm{D}} = {200^0}:2 = {100^0}.\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 1 trang 66 SGK Toán 8 Tập 1
Bài tập 2 trang 66 SGK Toán 8 Tập 1
Bài tập 4 trang 67 SGK Toán 8 Tập 1
Bài tập 5 trang 67 SGK Toán 8 Tập 1
Bài tập 1 trang 80 SBT Toán 8 Tập 1
Bài tập 2 trang 80 SBT Toán 8 Tập 1
Bài tập 3 trang 80 SBT Toán 8 Tập 1
Bài tập 4 trang 80 SBT Toán 8 Tập 1
Bài tập 5 trang 80 SBT Toán 8 Tập 1
Bài tập 6 trang 80 SBT Toán 8 Tập 1
Bài tập 7 trang 80 SBT Toán 8 Tập 1
Bài tập 8 trang 80 SBT Toán 8 Tập 1
Bài tập 9 trang 80 SBT Toán 8 Tập 1
Bài tập 10 trang 80 SBT Toán 8 Tập 1
Bài tập 1.1 trang 81 SBT Toán 8 Tập 1
-


Cho ABCD là hình bình hành tính diện tích ABCD biết diện tích \(ABH = 450m^2\)
bởi Diệu Hương
 13/01/2021
13/01/2021
cho ABCD là hình bình hành Tính diện tích ABCD biết diện tích ABH = 450 m2
Theo dõi (0) 0 Trả lời -

Tam giác ABC có diện tích = S. D nằm trên AB sao cho AD = 2BD. E là trung điểm AC. CD cắt BE tại I. Diện tích tam giác BIC = bao nhiêu lần S?
bởi Võ Lê Anh Minh
 03/01/2021
03/01/2021
Tam giác ABC có diện tích = S. D nằm trên AB sao cho AD = 2 BD. E là trung điểm AC. CD cắt BE tại I. Diện tích tam giác BIC = bao nhiêu lần S?
P/S : Cảm ơn các bạn!
Theo dõi (0) 3 Trả lời -


cho hình tứ giác ABCD.gọi M là giao điểm của 2 tia BA và CD và N vào giao của 2 tia AD,BC.các tai phân giác của góc BMCvaf BNA cắt nhau tại I. Tính góc MNI theo các góc A,B,C,D của tứ giác ABCD
bởi Duy Tùng
 10/09/2020
10/09/2020
cho hình tứ giác ABCD.gọi M là giao điểm của 2 tia BA và CD và N vào giao của 2 tia AD,BC.các tai phân giác của góc BMCvaf BNA cắt nhau tại I
a,Tính góc MNI theo các góc A,B,C,D của tứ giác ABCD
b,Tìm mối quan hệ giữa các góc A,B,C,D của tứ giác ABCD để có IM vuông góc với IM
Theo dõi (1) 2 Trả lời -


Chứng minh rằng các góc của một tứ giác không thể đều là góc nhọn, không thể đều là góc tù.
bởi Huệ Trần
 10/09/2020
Phần bài tập hình học
10/09/2020
Phần bài tập hình học Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Cho tứ giác ABCD có BC = AD, đường trung trực của AB và CD cắt nhau tại E. Chứng minh góc EAB = góc EDC
bởi Không Tên
 05/09/2020
05/09/2020
Cho tứ giác ABCD có BC = AD, đường trung trực của AB và CD cắt nhau tại E.Chứng minh góc EAB = góc EDC.Giải nhanh dùm mình nha!
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác IEJF có các góc đối bù nhau?
bởi linh
 04/09/2020
04/09/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính số đo góc A và góc C?
bởi Không Tên
 04/09/2020
04/09/2020
Cho tứ giác ABCD,góc A + góc C =1900 ,I là giao điểm 2 phân giác góc B và góc D sao cho góc BID =1450 .Tính số đo góc A và góc C .Giải nhanh dùm mình nha!
Theo dõi (0) 3 Trả lời -


Cho tứ giác ABCD có AC=AD, chứng minh BC
bởi Ác Quỷ
 24/08/2020
24/08/2020
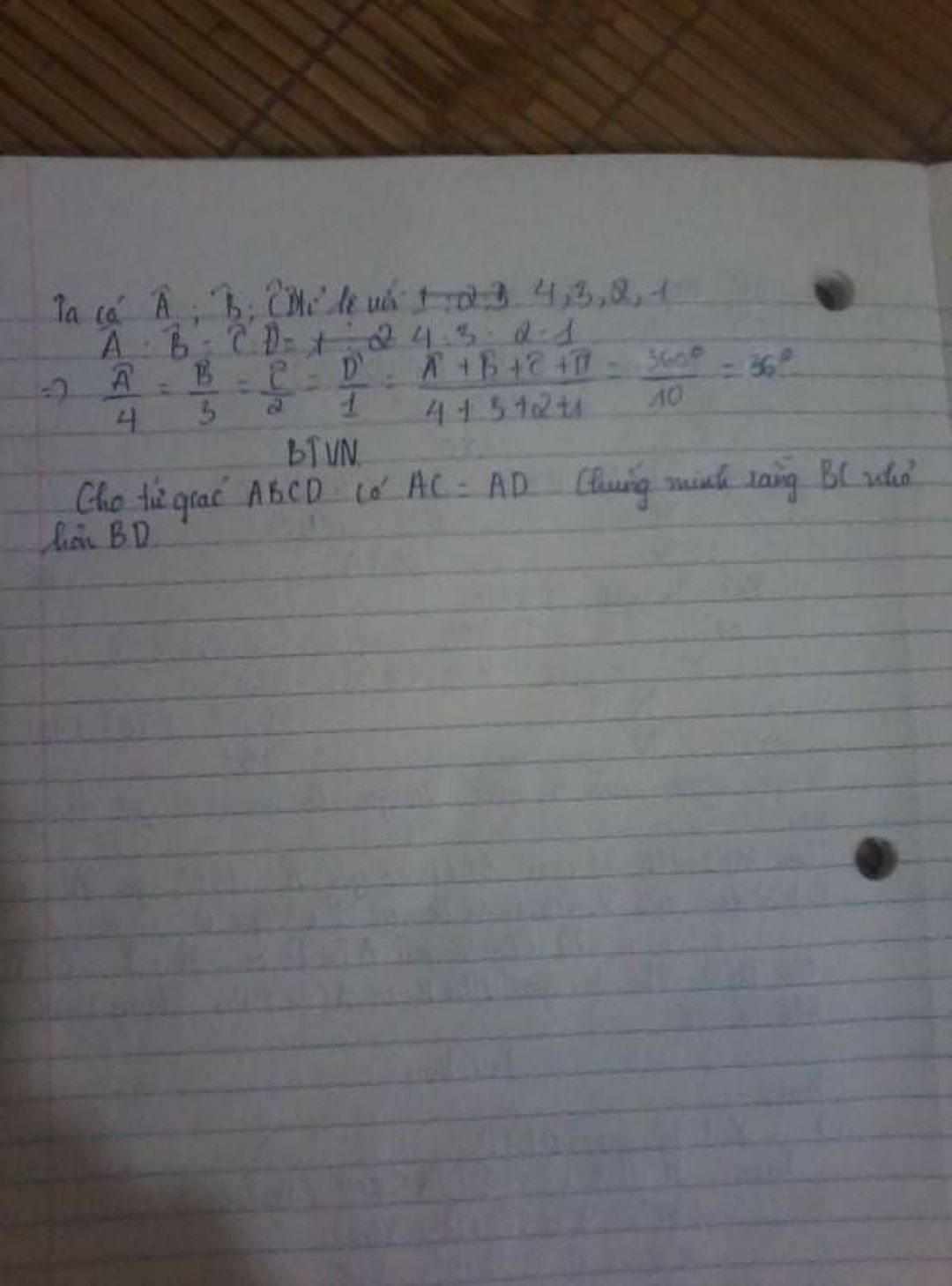 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng tỏ rằng MP + NQ > MN + PQ?
bởi Hoàng Linh
 21/08/2020
21/08/2020
Cho tứ giác MNPQ , G là giao điểm của hai đường chéo MP và NQ . Chứng tỏ rằng :
a) MP + NQ > MN + PQ
b ) MP + NQ > MQ + NP
Theo dõi (0) 7 Trả lời -


Chứng minh \(\dfrac{BC+ AD}{2} >MN\)?
bởi Linh Tran
 11/08/2020
11/08/2020
Cho tứ giác ABCD. Gọi M, N theo thứ tự là trung điểm của AB và CD và I là trung điểm của MN. Chứng minh BC AD ÷2 >MN
Theo dõi (0) 0 Trả lời -


Tứ giác ABCD có các tia phân giác của góc A và góc B cắt nhau ở I và góc C - góc D = 20 độ thì góc C và D có số đo bằng bao nhiêu?
bởi Cấn Phương Anh
 05/08/2020
05/08/2020
Lv4
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Chứng minh AC là tia phân giác của Góc BAD?
bởi nguyễn đặng ý viên
 30/07/2020
30/07/2020
Cho tứ giác lồi ABCD có góc B góc D=180 độ ,CB=CD. Chứng minh AC là tia phân giác của Góc BAD?
Theo dõi (1) 4 Trả lời -


Tính số đo các góc của từ giác ABCD?
bởi Châu Anh
 25/07/2020
25/07/2020
Bài 1: Cho tứ giác ABCD có góc B + góc C = 180 độ. Tính tổng góc A + góc D. Giả sử góc A = 1/5 góc D, góc B - góc C = 10 độ. Tính số đo mỗi góc.
Bài 2: Cho tứ giác ABCD có góc B = góc C = 120 độ. Phân giác của góc A và phân giác của góc D cắt nhau tại E, phân giác góc ngoài tại góc A và góc D cắt nhau tại F. Tính góc AED và góc AFD
Theo dõi (0) 3 Trả lời -


Chứng minh AB vuông góc vói BC?
bởi Trang Lê
 23/07/2020
23/07/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời





