Giải bài 2 tr 80 sách BT Toán lớp 8 Tập 1
Tứ giác \(ABCD\) có \(AB=BC, CD=DA.\)
\(a)\) Chứng minh rằng \(BD\) là đường trung trực của \(AC\)
\(b)\) Cho biết \(\widehat B = {100^0},\widehat D = {70^0}\) tính \(\widehat A\) và \(\widehat C\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
\(a)\) Sử dụng tính chất đường trung trực của đoạn thẳng.
\(b)\) Tổng bốn góc của một tứ giác bằng \(360^o.\)
Lời giải chi tiết
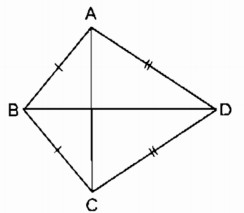
\(a)\) Ta có: \(BA=BC\) (gt)
\(\Rightarrow \) điểm \(B\) thuộc đường trung trực của \( AC\)
Lại có: \(DA=DC\) (gt)
\(\Rightarrow\) điểm \(D\) thuộc đường trung trực của \(AC\)
\(B\) và \(D\) là hai điểm phân biệt cùng thuộc đường trung trực của \(AC\) nên đường thẳng \(BD\) là đường trung trực của \(AC.\)
\(b)\) Xét \( ∆ BAD\) và \(∆ BCD,\) ta có:
\(BA = BC\) (gt)
\(DA = DC\) (gt)
\(BD\) cạnh chung
Do đó \(∆ BAD =∆ BCD (c.c.c)\) \(\Rightarrow \widehat {BAD} = \widehat {BCD}\) (hai góc tương ứng)
Ta có: \( \widehat {BAD} + \widehat {BCD} + \widehat {ABC} + \widehat {ADC}\)\( = {360^0} \) (tổng 4 góc trong tứ giác)
\(\Rightarrow \widehat {BAD} + \widehat {BCD}\)\( = {360^0} - \left( {\widehat {ABC} + \widehat {ADC}} \right)\)
\(\Rightarrow \widehat {BAD} + \widehat {BAD}\)\(= {360^0} - \left( {{{100}^0} + {{70}^0}} \right) \)
\(\Rightarrow 2\widehat {BAD} = {190^0} \)
\(\Rightarrow \widehat {BAD} = {190^0}:2 = {95^0}\)
\(\Rightarrow \widehat {BCD} = \widehat {BAD} = {95^0}\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 5 trang 67 SGK Toán 8 Tập 1
Bài tập 1 trang 80 SBT Toán 8 Tập 1
Bài tập 3 trang 80 SBT Toán 8 Tập 1
Bài tập 4 trang 80 SBT Toán 8 Tập 1
Bài tập 5 trang 80 SBT Toán 8 Tập 1
Bài tập 6 trang 80 SBT Toán 8 Tập 1
Bài tập 7 trang 80 SBT Toán 8 Tập 1
Bài tập 8 trang 80 SBT Toán 8 Tập 1
Bài tập 9 trang 80 SBT Toán 8 Tập 1
Bài tập 10 trang 80 SBT Toán 8 Tập 1
Bài tập 1.1 trang 81 SBT Toán 8 Tập 1
-


Cho tam giác vuông góc tại A AM là trung tuyến D là trung điểm AB E đối xứng M qua D
bởi Đào Thị Nhàn
 03/05/2018
03/05/2018
cho tam giác vuông góc tại A AM là trung tuyến D là trung điểm AB E đối xứng M qua D
a) Chứng minh E đối xứng với M qua AB
b) AEBM là hình gì Vì sao
c) tam giác ABC vuông cân điều kiện gì để AEMB là hình vuông
LÀM GIÚP MÌNH VỚI NHA NGÀY MAI MÌNH CÓ BAI KIỂM TRA RỒI HU HU
Theo dõi (0) 1 Trả lời -


Cho tam g iác ABC có trung tuyến AM lấy điểm E trên AC sao cho AE=1/3 AC
bởi Trần Thị Trang
 27/01/2018
27/01/2018
Cho tam giác ABC có trung tuyến AM lấy điểm E trên AC sao cho AE=1/3 AC; BE cắt AM tại D
a) Chứng minh rằng D là trung điểm của AM
b) Kẻ CD cắt AB tại E chứng minh rằng EF//BC
Theo dõi (0) 1 Trả lời -


Tứ giác ABCD có góc B + góc D = 180\(^0\) , CB=CD. Trên tia đối của tia DA lấy điểm E sao cho DE = AB . CM :
a, \(\Delta\) ABC = \(\Delta\) EDC
b, AC là tia p/g của góc BAD
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, lấy các điểm D, E theo thứ tự trên các cạnh AB,Ac sao cho BD = CE. Gọi M,N,I,K lần lượt là trung điểm các cạnh BE,CD,DE,BC
Chứng minh : IK ⊥ MN
( không cần vẽ hình )
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm
bởi Lê Thánh Tông
 29/03/2018
29/03/2018
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Đường trung tuyến AM; qua M lần lượt kẻ các đường thẳng vuông góc với AB và AC tại E và F.
a, Tính độ dài BC và AM
b, Chứng minh rằng tứ giác AEMF là hình chữ nhật.
c, Lấy điểm D đối xứng với M qua F. Chứng minh rằng tứ giác MCDA là hình thoi.
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A có đường cao AH
bởi Mai Rừng
 23/05/2018
23/05/2018
Cho tam giác ABC vuông tại A có đường cao AH. Biết AC=3cm, AB=4cm. Từ H kẻ HN⊥ AC, kẻ HM⊥AB
a) c/m tứ giác AMHN là hình chữ nhật
b) Gọ D là điểm đối xứng với H qua M, E đối xứng với H qua N. C/m tứ giác AMNE là hình bình hành
c) c/m A là trung điểm của DE
d) Tính độ dài đường cao AH của tam giác ABC
Theo dõi (0) 1 Trả lời -


Cho hình thang vuông ABCD với góc A bằng góc B bằng 90 độ AD=2BC
a) Kẻ CK vuông góc với AD tại K Tứ giác ABCK là hình gì? Tại sao?
b) Gọi AH là đường cao của tam giác ABC. E và F lần lượt là trung điểm của AH và DH chứng minh rằng tứ giác BCFE là hình bình hành
c) Chứng minh BE vuông góc với AF
Theo dõi (0) 1 Trả lời -


Cho hình bình hành ABCD. Gọi E,F tương ứng là trung điểm của CD và AB.
a) CMR: AECF LÀ HÌNH BÌNH HÀNH
b) AE cắt BD tại I, còn CF cắt BD tại H. CMR DI=IH=HB
c) Gọi J là giao điểm của BE với CF. CMR 4HJ=HC
ĐANG CẦN GẤP MAI NỘP RỒI!!!!
Theo dõi (0) 1 Trả lời -


Cho tứ giác ABCD gọi I,K,M,N lần lượt là trung điểm của AB, BC, CD, DA
a, C/M IKMN là hình bình hành
b, các đường chéo AC, BD của tứ giác ABCD cần có điều kiện gì để IKMN là HCN và hình thoi
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC đường cao AH M là điểm bất kì trên cạnh BC qua M kẻ các đường thẳng song song với AB và AC chúng cắt các cạnh AC và AB theo thứ tự ở E và D
Tứ giác AEMD là hình gì vì sao
2 đường chéo AM và DE cắt nhau tại I . Cm tam giác AIH cân
Tìm điều kiện để tứ giác ADME là hình vuông
Giúp em với ạ
Theo dõi (0) 1 Trả lời -


Cho hình bình hành ABCD có cạnh AD=a và AB =2a
bởi cuc trang
 17/01/2018
17/01/2018
C ho hình bình hành ABCD có cạnh AD=a và AB =2a . Gọi M ,N lần lượt là trunh điểm của AB và CD
1, Chứng minh tam giác ADN cân và AN là phân giác của góc BAD
2, Chứng minh MD//NB
3, Gọi P là giao điểm của AN vs DM , Q là giao điểm của CM với BN . chứng minh tứ giac PMQN là hình chữ nhật
Theo dõi (0) 1 Trả lời -


Cho tam giác nhọn ABC , các đường cao BD , CE cắt nhau tại H . Chứng minh rằng BH . BD + CH . CE = \(BC^2\)
Theo dõi (0) 1 Trả lời -


Tính độ dài cạnh BC và AM biết tam giác ABC vuông tại A có AM là trung tuyến
bởi Nguyễn Trà Long
 17/06/2018
17/06/2018
Cho tam giác ABC (A=90) AM là trung tuyến. Biết AB=3cm,AC=4cm
a) Tính độ dài cạnh BC và AM
b) Gọi D là điểm đối xứng với A qua M. Tứ giác ABDC là hình gì?vì sao?
c) Gọi E là điểm đối xứng với M qua AC. Chứng minh tứ giác AMCE là hình thoi
d) Tìm điều kiện của tam giác ABC để tứ giác AMCE là hình vuông
( cho mình hình vẽ nữa nha )
Theo dõi (0) 1 Trả lời -


Chứng minh AA’ = BB’ + CC’ biết qua trọng tâm tam giác kẻ đường thẳng d sao cho B và C nằm cùng phía với d
bởi het roi
 30/03/2018
30/03/2018
Cho ABC , qua trọng tâm của tam giác kẻ đường thẳng d sao cho B và C nằm cùng phía đối với d. Gọi AA’; BB’; CC’ là các đường vuông góc kẻ từ A, B, C đến đường thẳng d. CMR: AA’ = BB’ + CC’
Theo dõi (0) 1 Trả lời





