Giải bài 17 tr 75 sách GK Toán 8 Tập 1
Hình thang ABCD (AB // CD) có \(\widehat{ACD}=\widehat{BDC}\). Chứng minh rằng ABCD là hình thang cân.
Hướng dẫn giải chi tiết
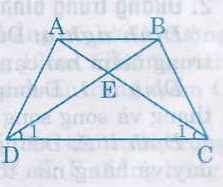
Gọi \(E\) là giao điểm của \(AC\) và \(BD.\)
Xét \(∆ECD\) có: \(\widehat {{C_1}} = \widehat {{D_1}}\) (giả thiết)
\(\Rightarrow \Delta EC{\rm{D}}\) cân tại \(E\) (dấu hiệu nhận biết tam giác cân).
\( \Rightarrow EC = E{\rm{D}}\) (tính chất tam giác cân) (1)
Ta có:
\({\rm{AB//DC}}\left( \text{giả thiết} \right) \)\(\;\Rightarrow \left\{ \begin{array}{l}
\widehat {BA{\rm{E}}} = \widehat {{C_1}}\\
\widehat {AB{\rm{E}}} = \widehat {{D_1}}
\end{array} \right.\left( \text{so le trong} \right)\)
Mà: \(\widehat {{C_1}} = \widehat {{D_1}}\left( \text{giả thiết} \right) \Rightarrow \widehat {BA{\rm{E}}} = \widehat {AB{\rm{E}}}\) \( \Rightarrow \Delta ABE\) cân tại \(E\) (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow AE = BE\) (tính chất tam giác cân) (2)
Lại có:
\(\left\{ \begin{array}{l}
AC = A{\rm{E}} + EC\\
B{\rm{D}} = BE + DE
\end{array} \right.\;\left( 3 \right)\)
Từ (1), (2) và (3) suy ra \(AC = BD.\)
Suy ra hình thang \(ABCD\) là hình thang cân (dấu hiệu nhận biết hình thang).
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 15 trang 75 SGK Toán 8 Tập 1
Bài tập 16 trang 75 SGK Toán 8 Tập 1
Bài tập 18 trang 75 SGK Toán 8 Tập 1
Bài tập 19 trang 75 SGK Toán 8 Tập 1
Bài tập 22 trang 82 SBT Toán 8 Tập 1
Bài tập 23 trang 82 SBT Toán 8 Tập 1
Bài tập 24 trang 83 SBT Toán 8 Tập 1
Bài tập 25 trang 83 SBT Toán 8 Tập 1
Bài tập 26 trang 83 SBT Toán 8 Tập 1
Bài tập 27 trang 83 SBT Toán 8 Tập 1
Bài tập 28 trang 83 SBT Toán 8 Tập 1
Bài tập 29 trang 83 SBT Toán 8 Tập 1
Bài tập 30 trang 83 SBT Toán 8 Tập 1
Bài tập 31 trang 83 SBT Toán 8 Tập 1
Bài tập 32 trang 83 SBT Toán 8 Tập 1
Bài tập 33 trang 83 SBT Toán 8 Tập 1
Bài tập 3.1 trang 83 SBT Toán 8 Tập 1
-


cho hình thang ABCD ( AB//CD) . gọi E là trung điểm của AB , F là trung điểm của CD , O là trung điểm của EF , qua O kẻ đường thẳng // CD , cắt AD và BC theo thứ tự ở M và N
A) cm M là trung điểm của AD
N là trung điểm của BC
b) cm OM = ON
c) tứ giác EMFN là hình gì ? vì saoTheo dõi (0) 1 Trả lời -


Chứng minh nếu 2 tia phân giác xủa góc A và góc B cắt nhau tại điểm K thuộc đáy CD thì AD + BC = DC
bởi Nguyễn Thị Thu Huệ
 31/05/2019
31/05/2019
Cho hình thang ABCD có AB // CD. Chứng minh :
a) Nếu 2 tia phân giác xủa góc A và góc B cắt nhau tại điểm K thuộc đáyCD thì AD + BC = DC
b) Nếu 2 tia phân giác của góc A và góc D cùng đi qua trung điểm F của cạnh bên BC thì cạnh bên AD bằng tổng 2 cạnh đáy
Theo dõi (0) 1 Trả lời -


Chứng minh MNPB là hình bình hành biết ABC có AB
bởi hai trieu
 31/05/2019
31/05/2019
cho tam giác ABC có AB < AC đường cao AH . gọi M ,N , P lần lượt là trung điểm của AB, AC , BC
a) cm MNPB là hình bình hành
b) cm MNPH là hình thang cân
c) gọi K là điểm đối xứng với N qua BC, và I là trung điểm của HP . cm M, I ,K thẳng hàngTheo dõi (0) 1 Trả lời -


Chứng minh EFIK là hình thang cân và KF= 1/2 CD
bởi Bin Nguyễn
 31/05/2019
31/05/2019
trên đoạn thẳng AB lấy M( MA>MB ) trên cừng một nữa mặt phẳng bờ AB vẽ các tam giác đều AMC; BMD. gọi E,F,I,K theo thứ tự là trung điểm của CM,CB,DM,DA. Chứng minh : EFIK là hình thang cân và KF= 1/2 CD
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho hình thang ABCD (AB//CD). Cm góc ACD= góc BDC
Theo dõi (0) 1 Trả lời -


1/ Cho hình thang cân ABCD (AB//CD) 2 đường chéo cắt nhau tại O. CM:
OA=OB, OC=OD
2. Cho hình thang cân ABCD (AB//CD) có góc A= 2 lần góc D. Tính các góc của hình thang
3.Cho tam giác ABC cân tại A, kẻ các đường cao BD, CE. CM: Tứ giác BEDC là hình thanh cân
Theo dõi (0) 1 Trả lời





