Giải bài 24 tr 83 sách BT Toán lớp 8 Tập 1
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN.
a. Tứ giác BMNC là hình gì ? Vì sao ?
b. Tính các góc của tứ giác BMNC biết rằng \(\widehat A = {40^0}\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Hình thang là tứ giác có hai cạnh đối song song.
+) Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Lời giải chi tiết
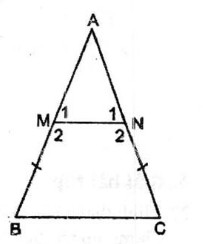
a. ∆ ABC cân tại A
\( \Rightarrow \widehat B = \widehat C = {{{{180}^0} - \widehat A} \over 2}\) (tính chất tam giác cân) (1)
AB = AC (gt)
⇒ AM + BM= AN+ CN
⇒ mà BM = CN (gt)
⇒ suy ra: AM = AN
⇒ ∆ AMN cân tại A
\( \Rightarrow {\widehat M_1} = {\widehat N_1} = {{{{180}^0} - \widehat A} \over 2}\) ( tính chất tam giác cân) (2)
⇒ Từ (1) và (2) suy ra: \({\widehat M_1} = \widehat B\)
⇒MN // BC ( vì có các cặp góc đồng vị bằng nhau)
Tứ giác BCMN là hình thang có \(\widehat B = \widehat C\). Vậy BCMN là hình thang cân.
b. \(\widehat B = \widehat C = {{{{180}^0} - \widehat A} \over 2} = {{{{180}^0} - {{40}^0}} \over 2} = {70^0}\)
Mà \({\widehat M_2} + \widehat B = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow {\widehat M_2} = {180^0} - \widehat B = {180^0} - {70^0} = {110^0}\)
\({\widehat N_2} = {\widehat M_2} = {110^0}\) (tính chất hình thang cân)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 22 trang 82 SBT Toán 8 Tập 1
Bài tập 23 trang 82 SBT Toán 8 Tập 1
Bài tập 25 trang 83 SBT Toán 8 Tập 1
Bài tập 26 trang 83 SBT Toán 8 Tập 1
Bài tập 27 trang 83 SBT Toán 8 Tập 1
Bài tập 28 trang 83 SBT Toán 8 Tập 1
Bài tập 29 trang 83 SBT Toán 8 Tập 1
Bài tập 30 trang 83 SBT Toán 8 Tập 1
Bài tập 31 trang 83 SBT Toán 8 Tập 1
Bài tập 32 trang 83 SBT Toán 8 Tập 1
Bài tập 33 trang 83 SBT Toán 8 Tập 1
Bài tập 3.1 trang 83 SBT Toán 8 Tập 1
-


cho hình thang cân ABCD ( AB//CD) . Gọi M là giao điểm của AC và BD . Chứng minh rằng :
a) MA=MB
b)MC=MD
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A trên tia đối của tia AC lấy điểm D .Trên tia đối của tia AB lấy điểm E sao choAD=AE.Chứng minh DECB là hình thang cân.Giải giùm nha, mơn...
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác BMDC là hình thang cân biết tam giác ABC cân tại A lấy M thuộc AB
bởi Lê Minh Trí
 31/05/2019
31/05/2019
Cho tam giác ABC cân tại A, lấy M bất kì thuộc cạnh AB. Trên tia đối tia CA lấy N sao cho CN=BM. Vẽ ME và NE lần lượt vuông góc với đường thẳng BC. Gọi Ilaf giao điểm của MN và BC. Trên AC lấy diểm D sao cho CD=CN.
a, Chứng minh: IE=IF
b, Chứng minh: tứ giác BMDC là hình thang cân
Theo dõi (0) 1 Trả lời -


Tính các góc của tứ giác BEDE biết tam giác ABC cân tại A có BD, CE là tia phân giác
bởi Nguyễn Hoài Thương
 31/05/2019
31/05/2019
Cho tam giác ABC cân tại A, kẻ phân giác BD, CE
a) BDCE là hình gì?
b) DE=ED=DC
c) biết A=80*. Tính các góc của tứ giác BEDC
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh BFEC là hình thang cân biết tam giác ABC cân tại A có đường cao AH, BE, CF
bởi Co Nan
 31/05/2019
31/05/2019
16 Cho tam giác ABC cân tại A , các đường cao AH,BE,CF. Chứng minh rằng BFEC là hình thang cân
Theo dõi (0) 1 Trả lời -


Chứng minh DB là tia phân giác của góc D biết tứ giác ABCD có D=AB=BC và góc A+góc C=180 độ
bởi thùy trang
 31/05/2019
31/05/2019
Giúp mình bài này với. Cho tứ giác ABCD biết AD=AB=BC và góc A+góc C=180 độ. CMR:
a)DB là tia phân giác của góc D
b)ABCD là hình thang cân
Theo dõi (0) 1 Trả lời






