Giải bài 30 tr 83 sách BT Toán lớp 8 Tập 1
Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.
a. Tứ giác BDEC là hình gì ? Vì sao ?
b. Các điểm D, E ở vị trí nào thì BD = DE = EC ?
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Hình thang là tứ giác có hai cạnh đối song song.
+) Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
Lời giải chi tiết
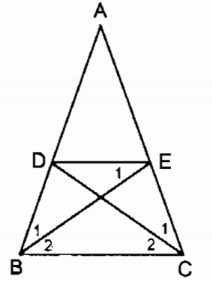
a. AD = AE (gt)
⇒ ∆ ADE cân tại A
\( \Rightarrow \widehat {ADE} = {{{{180}^0} - \widehat A} \over 2}\)
∆ ABC cân tại A
\( \Rightarrow \widehat {ABC} = {{{{180}^0} - \widehat A} \over 2}\)
Suy ra: \(\widehat {ADE} = \widehat {ABC}\)
⇒ DE // BC (vì có cặp góc đồng vị bằng nhau)
Tứ giác BDEC là hình thang
\(\widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)
Hay \(\widehat {DBC} = \widehat {ECB}\). Vậy BDEC là hình thang cân
b. Ta có: BD = DE ⇒ ∆ BDE cân tại D
\( \Rightarrow {\widehat B_1} = {\widehat E_1}\)
Mà \({\widehat E_1} = {\widehat B_2}\) (so le trong)
\( \Rightarrow {\widehat B_1} = {\widehat B_2}\)
DE = EC ⇒∆ DEC cân tại E
\( \Rightarrow {\widehat D_1} = {\widehat C_1}\)
\({\widehat D_1} = {\widehat C_2}\) (so le trong)
\( \Rightarrow {\widehat C_1} = {\widehat C_2}\)
Vậy khi BE là tia phân giác của \(\widehat {ABC}\), CD là tia phân giác của \(\widehat {ACB}\) thì BD = DE = EC.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Chứng minh BEDC là hình thang cân biết tam giác ABC cân tại A có 2 đường phân giác BD, CE
bởi thu phương
 31/05/2019
31/05/2019
Cho \(\Delta ABC\) cân tại A hai đường phân giác BD, CE của \(\widehat{B}\), \(\widehat{C}\)
a ) \(\Delta ADE\) là tam giác gì ? Vì sao ?
b ) Chứng minh BEDC là hình thang cân.
c ) Chứng minh BE = DE = CD
Theo dõi (0) 1 Trả lời -


Cho hình thang cân ABCD(ABsong song CD)AB<CD kẻ các đường cao AE ,BF của hình thang . Chứng minh rằng DE=CF
Theo dõi (0) 1 Trả lời -


Chứng minh BNMC là hình thang cân biết tam giác ABC cân tại  có trung tuyến BM, CN
bởi truc lam
 31/05/2019
31/05/2019
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN. Chứng minh: BNMC là hình thang cân.
Theo dõi (0) 1 Trả lời -


ABCD là hình thang cân ( AB song song CD ), AC cắt BD tại E. CMR:
a) EA= EB; EC= ED
b) Kẻ đường cao AH, BK
CMR: DH= CK
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho \(\Delta\)OMN cân tại O trên các cạnh bên OM, ON lần lượt lấy các điểm Q, P sao cho OQ=OP.
a) Tứ giác MNPQ là hình gì? Vì sao?
Tính các góc của tứ giác MNPQ. Biết góc O=40 độ
Theo dõi (0) 1 Trả lời -


Tính độ dài đường trung bình của hình thang cân biết đường cao 10cm
bởi Nguyễn Thị Thu Huệ
 31/05/2019
31/05/2019
Cho hình thang cân có 2 đường chéo vuông góc và đường cao là 10cm Tính độ dài đường trung bình của hình thang cân
Theo dõi (0) 1 Trả lời






