Bài tập 25 trang 83 SBT Toán 8 Tập 1

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Hình thang là tứ giác có hai cạnh đối song song. 

+) Hình thâng cân là hình thang có hai góc kề một đáy bằng nhau.

Lời giải chi tiết

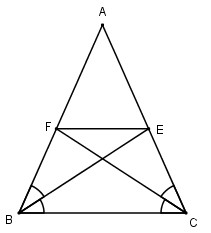
+) \(∆ ABC\) cân tại \(A\) nên \(AB = AC\)  và \(\widehat B=\widehat C\)

+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:

\(\widehat {ABE} =\displaystyle {{\widehat B} \over 2}\) và \(\displaystyle \widehat {ACF}= {{\widehat C} \over 2} \)

Suy ra \(\widehat {ABE}=\displaystyle {{\widehat B} \over 2} = {{\widehat C} \over 2} = \widehat {ACF}\)

Xét hai tam giác \(AEB\) và \(AFC\) có:

\(\widehat A\) là góc chung

\(AB = AC\) (chứng minh trên)

\(\widehat {ABE} = \widehat {ACF}\) (chứng minh trên)

\( \Rightarrow \Delta AEB = \Delta AFC\left( {g.c.g} \right)\)

\( \Rightarrow AE = AF \Rightarrow \Delta AEF\) cân tại \(A\)

\( \Rightarrow \widehat {AFE} =\displaystyle {{{{180}^0} - \widehat A} \over 2}\) 

Trong tam giác  \(\Delta ABC\) cân tại A có: \(\,\,\widehat B = \displaystyle {{{{180}^0} - \widehat A} \over 2}\)

\( \Rightarrow \widehat {AFE} = \widehat B\), mà hai góc ở vị trí đồng vị nên \( FE//BC\) 

\(\Rightarrow\) tứ giác \(BFEC\) là hình thang.

Ta có: \(\widehat B=\widehat C\) (tam giác \(ABC\) là tam giác cân tại \(A\))

\(\Rightarrow\) hình thang \(BFEC\) là hình thang cân.

Vì \(FE//BC\) \(\Rightarrow \widehat {FEB}=\widehat {CBE}\) (hai góc so le trong)

Mà \(\widehat {CBE}=\widehat {FBE}\) (\(BE\) là phân giác góc \(B\))

\(\Rightarrow \widehat {FBE}=\widehat {FEB}\)

\(\Rightarrow \Delta BFE\) là tam giác cân tại \(F\)

\(\Rightarrow EF=BF\) 

Vậy hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.

-- Mod Toán 8 HỌC247