Phß║ºn hã░ß╗øng dß║½n giß║úi b├ái tß║¡p To├ín 11 Chã░ãíng 3 B├ái 2 D├úy sß╗æ sß║¢ gi├║p c├íc em nß║»m ─æã░ß╗úc phã░ãíng ph├íp v├á r├¿n luyß╗çn k─® n─âng c├íc giß║úi b├ái tß║¡p tß╗½ SGK ─Éß║íi sß╗æ v├á Giß║úi t├¡ch 11 Cãí bß║ún-N├óng cao.
-
Bài tập 1 trang 92 SGK Đại số & Giải tích 11
Viß║┐t n─âm sß╗æ hß║íng ─æß║ºu cß╗ºa c├íc d├úy sß╗æ c├│ sß╗æ hß║íng tß╗òng qu├ít un cho bß╗ƒi c├┤ng thß╗®c:
a) \(u_n =\frac{n}{2^{n}-1}\);
b) \(u_n =\frac{2^{n}-1}{2^{n}+1}\)
c) \(u_n =(1+\frac{1}{n})^{n}\);
d) \(u_n =\frac{n}{\sqrt{n^{2}+1}}\)
-
Bài tập 2 trang 92 SGK Đại số & Giải tích 11
Cho dãy số \(U_n\) , biết:
\(u_1 = -1; u_n+1 = u_n +3\) vß╗øi \(n \geq 1\).
a) Viết năm số hạng đầu của dãy số
b) Chß╗®ng minh bß║▒ng phã░ãíng ph├íp quy nß║íp: \(u_n = 3n -4.\)
-
Bài tập 3 trang 92 SGK Đại số & Giải tích 11
Dãy số un cho bởi: \(u_1 = 3; u_n+1 = \sqrt{1+u^{2}_{n}}, n\geq 1\).
a) Viết năm số hạng đầu của dãy số.
b) Dß╗▒ ─æo├ín c├┤ng thß╗®c sß╗æ hß║íng tß╗òng qu├ít v├á chß╗®ng minh c├┤ng thß╗®c ─æ├│ bß║▒ng phã░ãíng ph├íp quy nß║íp
-
Bài tập 4 trang 92 SGK Đại số & Giải tích 11
X├®t t├¡nh t─âng, giß║úm cß╗ºa c├íc d├úy sß╗æ un biß║┐t:
a) \(u_n=\frac{1}{n}-2\);
b) \(u_n =\frac{n-1}{n+1}\);
c) \(u_n = (-1)^n(2^n + 1)\)
d) \(u_n =\frac{2n+1}{5n+2}\).
- VIDEOYOMEDIA
-
Bài tập 5 trang 92 SGK Đại số & Giải tích 11
Trong c├íc d├úy sß╗æ sau, d├úy sß╗æ n├áo bß╗ï chß║Àn dã░ß╗øi, d├úy sß╗æ n├áo bß╗ï chß║Àn tr├¬n, d├úy sß╗æ n├áo bß╗ï chß║Àn?
a) \(u_n = 2n^2 -1\)
b) \(u_n =\frac{1}{n(n+2)}\)
c) \(u_n =\frac{1}{2n^{2}-1}\)
d) \(u_n = sinn + cosn\)
-
Bài tập 3.9 trang 117 SBT Toán 11
Viết năm số hạng đầu và khảo sát tính tăng, giảm của các dãy số (un) biết
a) un = 101 - 2n
b) un = 3n - 7
c) \({u_n} = \frac{{{3^n}\sqrt n }}{{{2^n}}}\)
d) \({u_n} = \frac{{{3^n}\sqrt n }}{{{2^n}}}\)
-
Bài tập 3.10 trang 117 SBT Toán 11
Trong c├íc d├úy sß╗æ (un) cho dã░ß╗øi ─æ├óy, d├úy sß╗æ n├áo bß╗ï chß║Àn dã░ß╗øi, bß╗ï chß║Àn tr├¬n v├á bß╗ï chß║Àn ?
a) \({u_n} = 2n - {n^2}\)
b) \({u_n} = n + \frac{1}{n}\)
c) \({u_n} = \sqrt {{n^2} - 4n + 7} \)
d) \({u_n} = \frac{1}{{{n^2} - 6n + 11}}\)
-
Bài tập 3.11 trang 118 SBT Toán 11
Cho dãy số (un) xác định bởi
\(\left\{ \begin{array}{l}
{u_1} = 5\\
{u_{n + 1}} = {u_n} + 3n - 2,\,\,\,n \ge 1
\end{array} \right.\)a) T├¼m c├┤ng thß╗®c t├¡nh (un) theo n ;
b) Chß╗®ng minh (un) l├á d├úy sß╗æ t─âng.
-
Bài tập 3.12 trang 118 SBT Toán 11
Cho d├úy sß╗æ (un) vß╗øi un = n2 - 4n + 3
a) Viß║┐t c├┤ng thß╗®c truy hß╗ôi cß╗ºa d├úy sß╗æ ;
b) Chß╗®ng minh d├úy sß╗æ bß╗ï chß║Àn dã░ß╗øi ;
c) Tính tổng n số hạng đầu của dãy đã cho.
-
Bài tập 3.13 trang 118 SBT Toán 11
Cho d├úy sß╗æ (un) vß╗øi un = 1 + (n - 1).2n
a) Viết năm số hạng đầu của dãy số ;
b) T├¼m c├┤ng thß╗®c truy hß╗ôi ;
c) Chß╗®ng minh (un) l├á d├úy sß╗æ t─âng v├á bß╗ï chß║Àn dã░ß╗øi.
-
Bài tập 3.14 trang 118 SBT Toán 11
Cho d├úy sß╗æ (un) thoß║ú m├ún ─æiß╗üu kiß╗çn: Vß╗øi mß╗ìi n Ôêê NÔêù th├¼
\(0 < {u_n} < 1\) và \({u_{n + 1}} < 1 - \frac{1}{{4{u_n}}}\)
Chß╗®ng minh d├úy sß╗æ ─æ├ú cho l├á d├úy giß║úm.
-
Bài tập 3.15 trang 118 SBT Toán 11
Cho d├úy sß╗æ (un) x├íc ─æß╗ïnh bß╗ƒi c├┤ng thß╗®c:
\(\left\{ \begin{array}{l}
{u_1} = 1\\
{u_{n + 1}} = {u_n} + 2n - 1,\,\,n \ge 1
\end{array} \right.\)Số hạng u4 là:
A. u3 + 7 B. 10 C. 12 D. u3 + 5
-
Bài tập 3.16 trang 118 SBT Toán 11
H├úy chß╗ìn d├úy sß╗æ bß╗ï chß║Àn trong c├íc d├úy sß╗æ (un) sau:
A. un = n2 + n - 1 B. un = 3n
C. un = sinn + cosn D. un = - 3n2 + 1
-
Bài tập 3.17 trang 118 SBT Toán 11
H├úy chß╗ìn d├úy sß╗æ bß╗ï chß║Àn trong c├íc d├úy sß╗æ (un) sau:
A. \(u_n = -3n + 1\) B. \(u_n = -2n^2 + n\)
C. \({u_n} = n + \frac{1}{n}\) D. \(u_n = \cos n + 1\)
-
Bài tập 9 trang 105 SGK Toán 11 NC
Tìm 5 số hạng đầu của mỗi dãy số sau:
a. D├úy sß╗æ (un) vß╗øi \({u_n} = \frac{{2{n^2} - 3}}{n}\)
b. D├úy sß╗æ (un) vß╗øi \({u_n} = {\sin ^2}\frac{{n\pi }}{4} + \cos \frac{{2n\pi }}{3}\)
c. D├úy sß╗æ (un) vß╗øi \({u_n} = {\left( { - 1} \right)^n}.\sqrt {{4^n}} \)
-
Bài tập 10 trang 105 SGK Toán 11 NC
T├¼m sß╗æ hß║íng thß╗® 3 v├á sß╗æ hß║íng thß╗® 5 cß╗ºa mß╗ùi d├úy sß╗æ sau :
a. Dãy số (un) xác định bởi:
u1 = 0 v├á \({u_n} = \frac{2}{{u_{n - 1}^2 + 1}}\) vß╗øi mß╗ìi n ÔëÑ 2;
b. Dãy số (un) xác định bởi:
u1 = 1, u2 = ÔêÆ2 v├á \({u_n} = {u_{n - 1}} - 2{u_{n - 2}}\) vß╗øi mß╗ìi n ÔëÑ 3.
-
Bài tập 11 trang 106 SGK Toán 11 NC
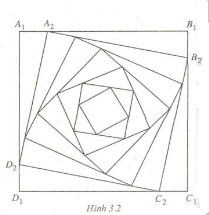
Cho h├¼nh vu├┤ng A1B1C1D1 c├│ c├íc cß║ính bß║▒ng 6cm. Ngã░ß╗Øi ta dß╗▒ng c├íc h├¼nh vu├┤ng A2B2C2D2, A3B3C3D3, ÔǪ, AnBnCnDn,ÔǪ theo c├ích sau: Vß╗øi mß╗ùi n = 2, 3, 4, ÔǪ lß║Ñy c├íc ─æiß╗âm An, Bn, Cn, v├á Dn tã░ãíng ß╗®ng tr├¬n c├íc cß║ính An-1Bn-1, Bn-1Cn-1, Cn-1Dn-1 v├á Dn-1An-1 sao cho An-1An = 1cm v├á AnBnCnDn l├á mß╗Öt h├¼nh vu├┤ng (h.3.2). X├®t d├úy sß╗æ (un) vß╗øi un l├á ─æß╗Ö d├ái cß║ính cß╗ºa h├¼nh vu├┤ng AnBnCnDn.
H├úy cho d├úy sß╗æ (un) n├│i tr├¬n bß╗ƒi hß╗ç thß╗®c truy hß╗ôi.
-
Bài tập 12 trang 106 SGK Toán 11 NC
Cho dãy số (un) xác định bởi :
u1 = 1 v├á un = 2unÔêÆ1+3 vß╗øi mß╗ìi n ÔëÑ 2.
Bß║▒ng phã░ãíng ph├íp quy nß║íp, chß╗®ng minh rß║▒ng vß╗øi mß╗ìi n ÔëÑ 1 ta c├│ un = 2n+1ÔêÆ3 (1)
-
Bài tập 13 trang 106 SGK Toán 11 NC
H├úy x├®t t├¡nh t─âng, giß║úm cß╗ºa c├íc d├úy sß╗æ sau :
a. D├úy sß╗æ (un) vß╗øi un = n3ÔêÆ3n2+5nÔêÆ7;
b. D├úy sß╗æ (xn) vß╗øi \({x_n} = \frac{{n + 1}}{{{3^n}}}\)
c. D├úy sß╗æ (an) vß╗øi \({a_n} = \sqrt {n + 1} - \sqrt n \)
-
Bài tập 14 trang 106 SGK Toán 11 NC
Chß╗®ng minh rß║▒ng d├úy sß╗æ (un) vß╗øi \({u_n} = \frac{{2n + 3}}{{3n + 2}}\) l├á mß╗Öt d├úy sß╗æ giß║úm v├á bß╗ï chß║Àn.
-
Bài tập 25 trang 109 SGK Toán 11 NC
Cho dãy số (un) xác định bởi
u1 = 3 v├á un+1 = un+5 vß╗øi mß╗ìi n ÔëÑ 1.
a. Hãy tính u2, u4 và u6.
b. Chß╗®ng minh rß║▒ng un = 5nÔÇô2 vß╗øi mß╗ìi n ÔëÑ 1.
-
Bài tập 16 trang 109 SGK Toán 11 NC
Cho dãy số (un) xác định bởi
u1 = 1 v├á un+1 = un+(n+1).2n vß╗øi mß╗ìi n ÔëÑ 1
a. Chß╗®ng minh rß║▒ng (un) l├á mß╗Öt d├úy sß╗æ t─âng.
b. Chß╗®ng minh rß║▒ng un = 1+(nÔêÆ1).2n vß╗øi mß╗ìi n ÔëÑ 1.
-
Bài tập 17 trang 109 SGK Toán 11 NC
Cho dãy số (un) xác định bởi
u1 = 1 v├á \({u_{n + 1}} = \frac{2}{{u_n^2 + 1}}\) vß╗øi mß╗ìi n ÔëÑ 1
Chß╗®ng minh rß║▒ng (un) l├á mß╗Öt d├úy sß╗æ kh├┤ng ─æß╗òi (d├úy c├│ tß║Ñt cß║ú c├íc sß╗æ hß║íng ─æß╗üu bß║▒ng nhau).
-
Bài tập 18 trang 109 SGK Toán 11 NC
Cho d├úy sß╗æ (sn) vß╗øi
\({s_n} = \sin \left( {4n - 1} \right)\frac{\pi }{6}\).
a. Chß╗®ng minh rß║▒ng sn = sn+3 vß╗øi mß╗ìi n ÔëÑ 1
b. Hãy tính tổng 15 số hạng đầu tiên của dãy số đã cho.


