Phần hướng dẫn giải bài tập Toán 10 Chương 3 Bài 3 Phương trình và hệ phương trình bậc nhất nhiều ẩn sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Đại số 10 Cơ bản và Nâng cao.
-
Bài tập 1 trang 68 SGK Đại số 10
Cho hệ phương trình \(\left\{\begin{matrix} 7x - 5 y = 9 & \\ 14x - 10y = 10& \end{matrix}\right.\). Tại sao không cần giải ta cũng kết luận được hệ phương trình này vô nghiệm ?
-
Bài tập 2 trang 68 SGK Đại số 10
Giải các hệ phương trình
a) \(\left\{\begin{matrix} 2x - 3y = 1 & \\ x + 2y = 3;& \end{matrix}\right.\)
b) \(\left\{\begin{matrix} 3x + 4y = 5 & \\ 4x - 2y = 2;& \end{matrix}\right.\)
c) \(\left\{ \begin{array}{l}\frac{2}{3}x + \frac{1}{2}y = \frac{2}{3}\\\frac{1}{3}x - \frac{3}{4}y = \frac{1}{2}\end{array} \right.\)
d) \(\left\{ \begin{array}{l}0,3x - 0,2y = 0,5\\0,5x + 0,4y = 1,2.\end{array} \right.\)
-
Bài tập 3 trang 68 SGK Đại số 10
Hai bạn Vân và Lan đến cửa hàng mua trái cây. Bạn Vân mua 10 quả quýt, 7 quả cam với giá tiền là 17 800 đồng. Bạn Lan mua 12 quả quýt, 6 quả cam hết 18 000 đồng. Hỏi giá tiền mỗi quả quýt và mỗi quả cam là bao nhiêu?
-
Bài tập 4 trang 68 SGK Đại số 10
Trong một xí nghiệp may có hai dây chuyền may áo sơ mi. Ngày thứ nhất cả hai dây chuyền may được 930 áo. Ngày thứ hai do dây chuyền thứ nhất tăng năng suất 18%, dây chuyền thứ hai tăng năng suất 15% nên cả hai dây chuyền may được 1083 áo. Hỏi trong ngày thứ nhất mỗi dây chuyền may được bao nhiêu áo sơ mi?
- VIDEOYOMEDIA
-
Bài tập 5 trang 68 SGK Đại số 10
Giải các hệ phương trình
a) \(\left\{\begin{matrix} x + 3y + 2z =8 & \\ 2x + 2y + z =6& \\ 3x +y+z=6;& \end{matrix}\right.\)
b) \(\left\{\begin{matrix} x - 3y + 2z =-7 & \\ -2x + 4y + 3z =8& \\ 3x +y-z=5.& \end{matrix}\right.\)
-
Bài tập 6 trang 68 SGK Đại số 10
Một cửa hàng bán áo sơ mi, quần âu nam và váy nữ. Ngày thứ nhất bán được 12 áo, 21 quần và 18 váy, doanh thu là 5 349 000 đồng. Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu là 5 600 000 đồng. Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu là 5 259 000 đồng. Hỏi giá bán mỗi áo, mỗi quần và mỗi váy là bao nhiêu?
-
Bài tập 7 trang 68 SGK Đại số 10
Giải các hệ phương trình sau bằng máy tính bỏ túi (làm tròn kết quả đến chữ số thập phân thứ hai)
a) \(\left\{\begin{matrix} 3x - 5y = 6 & \\ 4x + 7y =-8;& \end{matrix}\right.\)
b) \(\left\{\begin{matrix} -2x +3y = 5 & \\ 5x +2y = 4.& \end{matrix}\right.\)
c) \(\left\{\begin{matrix} 2x - 3y +4z=-5 & \\ -4x +5y-z=6& \\ 3x+4y-3z=7; & \end{matrix}\right.\)
d) \(\left\{\begin{matrix} -x+2y-3z=2 & \\ 2x +y+2z=-3& \\ -2x-3y+z=5. & \end{matrix}\right.\)
-
Bài tập 3.26 trang 73 SBT Toán 10
Một công ti có 85 xe chở khách gồm hai loại, xe chở được 4 khách và xe chở được 7 khách. Dùng tất cả số xe đó, tối đa công ti chở một lần được 445 khách. Hỏi công ti đó có mấy xe mỗi loại?
-
Bài tập 3.27 trang 73 SBT Toán 10
Giải các hệ phương trình
a) \(\left\{ \begin{array}{l}
x - 2y + z = 12\\
2x - y + 3z = 18\\
- 3x + 3y + 2z = - 9
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
x + y + z = 7\\
3x - 2y + 2z = 5\\
4x - y + 3z = 10
\end{array} \right.\) -
Bài tập 3.28 trang 74 SBT Toán 10
Giải các hệ phương trình sau bằng máy tính bỏ túi.
a) \(\left\{ \begin{array}{l}
\frac{3}{4}x - \frac{7}{3}y = \frac{4}{5}\\
\frac{2}{5}x + \frac{2}{7}y = \frac{2}{9}
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
3,7x + 4,3y = - 2,5\\
- 5,1x + 2,7y = 4,8
\end{array} \right.\) -
Bài tập 3.29 trang 74 SBT Toán 10
Giải các hệ phương trình sau bằng máy tính bỏ túi.
a) \(\left\{ \begin{array}{l}
3{x_1} + 4{x_2} - 5{x_3} = 12\\
- 4{x_1} + 2{x_2} + 7{x_3} = 7\\
5{x_1} + 6{x_2} - 4{x_3} = 12
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
0,3x - 4,7y + 2,3z = 4,9\\
- 2,1x + 3,2y + 4,5z = 7,6\\
4,2x + 2,7y + 3,7z = 5,7
\end{array} \right.\) -
Bài tập 3.30 trang 74 SBT Toán 10
Một chủ cửa hàng bán lẻ mang 1 500 000 đồng đến ngân hàng đổi tiền để trả lại cho người mua. Ông ta đổi được tất cả 1 450 đồng tiền xu các loại 2000 đồng, 1000 đồng và 500 đồng. Biết rằng số tiền xu loại 1 000 đồng bằng hai lần hiệu của số tiền xu loại 500 đồng với số tiền xu loại 2000 đồng. Hỏi mỗi loại có bao nhiêu đồng tiền xu?
-
Bài tập 3.31 trang 74 SBT Toán 10
Tìm giá trị của m để các hệ phương trình sau vô nghiệm:
a) \(\left\{ \begin{array}{l}
3x + 2y = 9\\
mx - 2y = 2
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
2x - my = 5\\
x + y = 7
\end{array} \right.\) -
Bài tập 3.32 trang 74 SBT Toán 10
Hệ phương trình sau có nghiệm là:
\(\left\{ \begin{array}{l}
2x - 5y = - 1\\
3x + 4y = 7
\end{array} \right.\)A. \(x = \frac{{15}}{{23}},y = \frac{{ - 21}}{{23}}\)
B. \(x = - \frac{4}{3},y = - \frac{1}{3}\)
C. \(x = \frac{{31}}{{23}},y = \frac{{17}}{{23}}\)
D. x = 2, y = 1
-
Bài tập 3.33 trang 75 SBT Toán 10
Nghiệm của hệ phương trình sau là:
\(\left\{ \begin{array}{l}
- 0,3x + 0,5y = 2,1\\
0,2x - 0,7y = - 2,5
\end{array} \right.\)A. x = 2, y = -3 B. x = -2, y = 3
C. x = -1, y = -2 D. x = 1, y = 5
-
Bài tập 3.34 trang 75 SBT Toán 10
Hệ phương trình sau vô nghiệm khi tham số m nhận giá trị:
\(\left\{ \begin{array}{l}
4x + y = 7\\
mx - 3y = 2
\end{array} \right.\)A. m = 4 B. m = -3
C. m = 2 D. m = -12
-
Bài tập 3.35 trang 75 SBT Toán 10
Một công ti kinh doanh xe buýt có 35 xe gồm hai loại: loại xe chở được 45 khách và loại xe chở được 12 khách. Nếu dùng tất cả số xe đó tối đa công ti chở một lần được 1113 khách. Vậy công ti có số xe mỗi loại là:
A. 20 xe 45 chỗ, 15 xe 12 chỗ.
B. 17 xe 45 chỗ, 18 xe 12 chỗ.
C. 21 xe 45 chỗ, 14 xe 12 chỗ.
D. 19 xe 45 chỗ, 16 xe 12 chỗ.
-
Bài tập 3.36 trang 75 SBT Toán 10
Hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}
{3x - y - 2z = \frac{1}{2}}\\
{ - 2x + 2y + 3z = \frac{{17}}{6}}\\
{x + 3y - z = \frac{4}{3}}
\end{array}} \right.\) có nghiệm là:A. \(\left( {x;y;z} \right) = \left( {\frac{4}{3};\frac{1}{2};\frac{3}{2}} \right)\)
B. \(\left( {x;y;z} \right) = \left( {\frac{{ - 1}}{3};\frac{4}{3};\frac{1}{2}} \right)\)
C. \(\left( {x;y;z} \right) = \left( {\frac{1}{2};\frac{{ - 1}}{3};\frac{{ - 3}}{2}} \right)\)
D. \(\left( {x;y;z} \right) = \left( {\frac{{ - 4}}{3};\frac{{ - 1}}{2};\frac{2}{3}} \right)\)
-
Bài tập 3.37 trang 75 SBT Toán 10
Một khách sạn có 102 phòng gồm ba loại: phòng 3 người, phòng 2 người và phòng 1 người. Nếu đầy khách tất cả các phòng thì khách sạn đón được 211 khách. Còn nếu cải tạo lại các phòng bằng cách: sửa các phòng 2 người thành 3 người, còn phòng 3 người sửa lại thành phòng 2 người và giữ nguyện phòng 1 người thì tối đa một lần có thể đón 224 khách.
Vậy số phòng từng loại hiện nay của khách sạn là:
A. 50 phòng 3 người, 41 phòng 2 người, 11 phòng 1 người.
B. 32 phòng 3 người, 45 phòng 2 người, 25 phòng 1 người.
C. 41 phòng 3 người, 51 phòng 2 người, 10 phòng 1 người.
D. 25 phòng 3 người, 59 phòng 2 người, 18 phòng 1 người.
-
Bài tập 3.38 trang 76 SBT Toán 10
Một số có ba chữ số. Nếu lấy số đó chia cho tổng các chữ số của nó thì được thương là 17 và dư 5. Nếu đổi hai chữ số hàng chục và hàng trăm cho nhau thì được số mới mà chia cho tổng các chữ số của nó thì được thương là 30 và dư là 4. Nếu đổi hai chữ số hàng chục và hàng đơn vị của số mới này cho nhau thì được một số mà chia cho tổng các chữ số của nó thì được thương là 34 và dư là 3. Vậy số đã cho ban đầu là:
A. 172 B. 296
C. 124 D. 587
-
Bài tập 22 trang 84 SGK Toán 10 NC
Giải các phương trình
a) \(\frac{{2\left( {{x^2} - 1} \right)}}{{2x + 1}} = 2 - \frac{{x + 2}}{{2x + 1}}\)
b) \(\frac{{2x - 5}}{{x - 1}} = \frac{{5x - 3}}{{3x + 5}}\)
-
Bài tập 23 trang 84 SBT Toán 10 NC
Giải phương trình sau \(\frac{{m - 3}}{{x - 4}} = {m^2} - m - 6\) trong mỗi trường hợp sau:
a) m = 3
b) m ≠ 3
-
Bài tập 24 trang 84 SGK Toán 10 NC
Giải và biện luận các phương trình (a và m là những tham số)
a) \(\left| {2ax + 3} \right| = 5\)
b) \(\frac{{2mx - {m^2} + m - 2}}{{{x^2} - 1}} = 1\)
-
Bài tập 25 trang 85 SGK Toán 10 NC
Giải và biện luận các phương trình (m, a và k là tham số)
a) \(\left| {mx - x + 1} \right| = \left| {x + 2} \right|\)b) \(\frac{a}{{x + 2}} + \frac{1}{{x - 2a}} = 1\)
c) \(\frac{{mx - m - 3}}{{x + 1}} = 1\)
d) \(\frac{{3x + k}}{{x - 3}} = \frac{{x - k}}{{x + 3}}\)
-
Bài tập 26 trang 85 SGK Toán 10 NC
Giải và biện luận phương trình sau (m và a là những tham số)
a) \(\left( {2x + m - 4} \right)\left( {2mx - x + m} \right) = 0\)
b) \(\left| {mx + 2x - 1} \right| = \left| x \right|\)
c) \(\left( {mx + 1} \right)\sqrt {x - 1} = 0\)
d) \(\frac{{2a - 1}}{{x - 2}} = a - 2\)
e) \(\frac{{\left( {m + 1} \right)x + m - 2}}{{x + 3}} = m\)
f) \(\left| {\frac{{ax + 1}}{{x - 1}}} \right| = a\)
-
Bài tập 27 trang 85 SGK Toán 10 NC
Bằng cách đặt ẩn phụ, giải các phương trình sau:
a) \(4{x^2} - 12x - 5\sqrt {4{x^2} - 12x + 11} + 15 = 0\)
b) \({x^2} + 4x - 3\left| {x + 2} \right| + 4 = 0\)
c) \(4{x^2} + \frac{1}{{{x^2}}} + \left| {2x - \frac{1}{x}} \right| - 6 = 0\)
-
Bài tập 28 trang 85 SGK Toán 10 NC
Tìm các giá trị của tham số m sao cho phương trình sau có nghiệm duy nhất : |mx – 2| = |x + 4| (*)
-
Bài tập 29 trang 85 SGK Toán 10 NC
Với giá trị của a thì phương trình sau vô nghiệm ?
\(\frac{{x + 1}}{{x - a + 1}} = \frac{x}{{x + a + 2}}\)
-
Bài tập 33 trang 94 SGK Toán 10 NC
Giải và biện luận hệ phương trình
a) \(\left\{ \begin{array}{l}
x - my = 0\\
mx - y = m + 1
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
2ax + 3y = 5\\
\left( {a + 1} \right)x + y = 0
\end{array} \right.\) -
Bài tập 34 trang 94 SGK Toán 10 NC
Giải hệ phương trình sau (có thể dùng máy tính bỏ túi để kiểm tra kết quả - Xem bài đọc thêm trang 94)
\(\left\{ \begin{array}{l}
x + y + z = 11\\
2x - y + z = 5\\
3x + 2y + z = 24
\end{array} \right.\) -
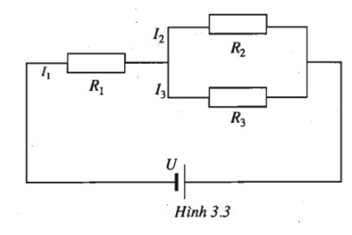
Bài tập 35 trang 94 SGK Toán 10 NC
Cho một mạch điện kín. Biết R1 = 0,250, R2 = 0,360, R3 = 0,450 và U = 0,6V. Gọi I1 là cường độ dòng điện của mạch chính, I2 và I3 là cường độ dòng diện của mạch rẽ. Tính I1, I2, I3 (chính xác đến phần trăm).
-
Bài tập 36 trang 96 SGK Toán 10 NC
Cho một hệ hai phương trình bậc nhất hai ẩn. Biết rằng phương trình thứ hai trong hệ vô nghiệm. Hãy chọn kết luận đúng trong các khẳng định sau:
(A) Hệ đã cho nghiệm đúng với mọi giá trị của ẩn;
(B) Hệ đã cho vô nghiệm;
(C) Tập nghiệm của hệ đã cho trùng với tập nghiệm của phương trình thứ nhất;
(D) Không có kết luận gì.
-
Bài tập 37 trang 97 SGK Toán 10 NC
Tính nghiệm gần đúng của hệ phương trình sau (chính xác đến hàng phần trăm):
a) \(\left\{ \begin{array}{l}
\sqrt 3 x - y = 1\\
5x + \sqrt 2 y = \sqrt 3
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
4x + \left( {\sqrt 3 - 1} \right)y = 1\\
\left( {\sqrt 3 + 1} \right)x + 3y = 5
\end{array} \right.\) -
Bài tập 38 trang 97 SGK Toán 10 NC
Một miếng đất hình chữ nhật có chu vi 2p (mét). Nếu mở rộng miếng đất đó bằng cách tăng một cạnh thêm 3m và cạnh kia thêm 2m thì diện tích miếng đất tăng thêm 246 m2. Tính các kích thước của miếng đất đó (biện luận theo p).
-
Bài tập 39 trang 97 SGK Toán 10 NC
Giải và biện luận các hệ phương trình
a) \(\left\{ \begin{array}{l}
x + my = 1\\
mx - 3my = 2m + 3
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
mx + y = 4 - m\\
2x + \left( {m - 1} \right)y = m
\end{array} \right.\) -
Bài tập 40 trang 97 SGK Toán 10 NC
Với giá trị nào của a thì mỗi hệ phương trình sau có nghiệm?
a) \(\left\{ \begin{array}{l}
\left( {a + 1} \right)x - y = a + 1\\
x + \left( {a - 1} \right)y = 2
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
\left( {a + 2} \right)x + 3y = 3a + 9\\
x + \left( {a + 4} \right)y = 2
\end{array} \right.\) -
Bài tập 41 trang 97 SGK Toán 10 NC
Tìm tất cả các cặp số nguyên (a, b) sao cho hệ phương trình sau vô nghiệm:
\(\left\{ \begin{array}{l}
ax + y = 2\\
6x + by = 4
\end{array} \right.\) -
Bài tập 42 trang 97 SGK Toán 10 NC
Cho hai đường thẳng (d1): x + my = 3 và (d2): mx + 4y = 6.
a) Với giá trị nào của m thì hai đường thẳng đó cắt nhau?
b) Với giá trị nào của m thì hai đường thẳng ấy song song với nhau?
c) Với giá trị nào của m thì hai đường thẳng ấy trùng nhau?
-
Bài tập 43 trang 97 SGK Toán 10 NC
Giải hệ phương trình
\(\left\{ \begin{array}{l}
x - y + z = 7\\
x + y - z = 1\\
- x + y + z = 3
\end{array} \right.\) -
Bài tập 44 trang 97 SGK Toán 10 NC
Bài toán máy bơm nước.
Một gia đình muốn mua một chiếc máy bơm nước. Có hai loại có cùng lưu lượng nước bơm được trong một giờ: loại thứ nhất giá 1,5 triệu đồng, loại thứ hai giá 2 triệu đồng. Tuy nhiên, nếu dùng máy bơm loại thứ nhất thì mồi giờ tiền điện phải trả là 1200 đồng, trong khi dùng máy bơm loại thứ hai thì phải trả 1000 đồng, cho mỗi giờ bơm.
Kí hiệu f(x) và g(x) lần lượt là số tiền (tính bằng nghìn đồng) phải trả khi sử dụng máy bơm loại thứ nhất và loại thứ hai trong X giờ (bao gồm tiền điện và tiền mua máy bơm).
a) Hãy biểu diễn f(x) và g(x) dưới dạng các biểu thức của X.
b) Vẽ đồ thị của y = f(x) và y = g(x) trên cùng một mặt phẳng tọa độ.
c) Xác định tọa độ giao điểm của hai đồ thị ấy. Hãy phân tích ý nghĩa kinh tế của giao điểm đó.
-
Bài tập 45 trang 100 SGK Toán 10 NC
Giải các hệ phương trình
a) \(\left\{ \begin{array}{l}
x - y = 2\\
{x^2} + {y^2} = 164
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
{x^2} - 5xy + {y^2} = 7\\
2x + y = 1
\end{array} \right.\) -
Bài tập 46 trang 100 SGK Toán 10 NC
Giải các hệ phương trình
a) \(\left\{ \begin{array}{l}
{x^2} + {y^2} + x + y = 8\\
xy + x + y = 5
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
{x^2} + {y^2} - x + y = 2\\
xy + x - y = - 1
\end{array} \right.\)c) \(\left\{ \begin{array}{l}
{x^2} - 3x = 2y\\
{y^2} - 3y = 2x
\end{array} \right.\) -
Bài tập 47 trang 100 SGK Toán 10 NC
Tìm quan hệ giữa S và P để hệ phương trình sau có nghiệm:
\(\left\{ \begin{array}{l}
x + y = S\\
xy = P
\end{array} \right.\)(S và P là hai số cho trước)
-
Bài tập 48 trang 100 SGK Toán 10 NC
Giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}
{x^2} + {y^2} = 208\\
xy = 96
\end{array} \right.\)b) \(\left\{ \begin{array}{l}
{x^2} - {y^2} = 55\\
xy = 24
\end{array} \right.\) -
Bài tập 49 trang 100 SGK Toán 10 NC
Tìm hàm số bậc hai y = f(x) thỏa mãn các điều kiện sau :
a) Parabol y = f(x) cắt trục tung tại điểm (0; - 4)
b) f(2) = 6
c) Phương trình f(x) = 0 có hai nghiệm và hiệu giữa nghiệm lớn và nghiệm bé bằng 5





