Bài tập 26 trang 85 SGK Toán 10 NC
Giải và biện luận phương trình sau (m và a là những tham số)
a) \(\left( {2x + m - 4} \right)\left( {2mx - x + m} \right) = 0\)
b) \(\left| {mx + 2x - 1} \right| = \left| x \right|\)
c) \(\left( {mx + 1} \right)\sqrt {x - 1} = 0\)
d) \(\frac{{2a - 1}}{{x - 2}} = a - 2\)
e) \(\frac{{\left( {m + 1} \right)x + m - 2}}{{x + 3}} = m\)
f) \(\left| {\frac{{ax + 1}}{{x - 1}}} \right| = a\)
Hướng dẫn giải chi tiết
a) Ta có \(\left( {2x + m - 4} \right)\left( {2mx - x + m} \right) = 0\)
\(\begin{array}{l}
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{2x + m - 4 = 0}\\
{2mx - x + m = 0}
\end{array}} \right.\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{{4 - m}}{2}}\\
{\left( {2m - 1} \right)x = - m}
\end{array}} \right.
\end{array}\)
+ Với \(m = \frac{1}{2}\) phương trình có nghiệm \(x = \frac{{4 - m}}{2} = \frac{7}{4}\)
+ Với \(m \ne \frac{1}{2}\) phương trình có 2 nghiệm: \(x = \frac{{4 - m}}{2};x = \frac{m}{{1 - 2m}}\)
b) Ta có \(\left| {mx + 2x - 1} \right| = \left| x \right|\)
\(\begin{array}{l}
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{mx + 2x - 1 = x}\\
{mx + 2x - 1 = - x}
\end{array}} \right.\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\left( {m + 1} \right)x = 1}\\
{\left( {m + 3} \right)x = 1}
\end{array}} \right.
\end{array}\)
+ Với m = - 1 phương trình có nghiệm \(x = \frac{1}{2}\)
+ Với m = - 3 phương trình có nghiệm \(x = -\frac{1}{2}\)
+ Với m ≠ - 1 và m ≠ - 3 thì phương trình có 2 nghiệm:
\(x = \frac{1}{{m + 1}};x = \frac{1}{{m + 3}}\)
c) Điều kiện: \(x \ge 1\)
\(\begin{array}{l}
\left( {mx + 1} \right)\sqrt {x - 1} = 0\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 1}\\
{mx + 1 = 0}
\end{array}} \right.{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)
\end{array}\)
+ Với m = 0, phương trình có nghiệm x = 1
+ Với m ≠ 0, \(\left( 1 \right) \Leftrightarrow x = - \frac{1}{m}\)
Kiểm tra điều kiện:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
- \frac{1}{m} \ge 1 \Leftrightarrow - \frac{1}{m} - 1 \ge 0\\
\Leftrightarrow \frac{{ - m - 1}}{m} \ge 0
\end{array}\\
{ \Leftrightarrow \frac{{m + 1}}{m} \le 0 \Leftrightarrow - 1 \le m < 0}
\end{array}\)
d) Điều kiện: \(x \ne 2\)
Ta có
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\frac{{2a - 1}}{{x - 2}} = a - 2\\
\Rightarrow 2a - 1 = \left( {a - 2} \right)\left( {x - 2} \right)
\end{array}\\
{ \Leftrightarrow \left( {a - 2} \right)x = 4a - 5\,\,\left( 1 \right)}
\end{array}\)
+ Với \(a=2\) thì \(S = \emptyset \)
+ Với \(a \ne 2\) thì \(\left( 1 \right) \Leftrightarrow x = \frac{{4a - 5}}{{a - 2}}\)
Kiểm tra điều kiện:
\(\begin{array}{l}
x \ne 2 \Leftrightarrow \frac{{4a - 5}}{{a - 2}} \ne 2\\
\Leftrightarrow 4a - 5 \ne 2a - 4\\
\Leftrightarrow a \ne \frac{1}{2}
\end{array}\)
Vậy:
+ Với \(a=2\) hoặc \(a = \frac{1}{2}:S = \emptyset \)
+ Với \(a \ne 2\) hoặc \(a \ne \frac{1}{2}:S = \left\{ {\frac{{4a - 5}}{{a - 2}}} \right\}\)
e) Điều kiện: \(x \ne - 3\)
Phương trình đã cho tương đương với:
\(\left( {m + 1} \right)x + m - 2 = m\left( {x + 3} \right) \)
\(\Leftrightarrow x = 2m + 2\)
x = 2m + 2 là nghiệm của phương trình
\( \Leftrightarrow 2m + 2 \ne - 3 \Leftrightarrow m \ne - \frac{5}{2}\)
Vậy
+ Với \(m \ne - \frac{5}{2}\) thì phương trình có nghiệm duy nhất x = 2m + 2
+ Với \(m = - \frac{5}{2}\) thì phương trình vô nghiệm
f) Rõ ràng \(a < 0\) thì phương trình vô nghiệm
Với \(a \ge 0\). Điều kiện \(x \ne 1\)
Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\left| {\frac{{ax + 1}}{{x - 1}}} \right| = a \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\frac{{ax + 1}}{{x - 1}} = a}\\
{\frac{{ax + 1}}{{x - 1}} = - a}
\end{array}} \right.\\
\Rightarrow \left[ {\begin{array}{*{20}{l}}
{ax + 1 = ax - a}\\
{ax + 1 = - ax + a}
\end{array}} \right.
\end{array}\\
{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{a = - 1{\mkern 1mu} {\mkern 1mu} \left( l \right)}\\
{2ax = a - 1}
\end{array}} \right.}
\end{array}\)
Vậy
+ Với \(a=0\): \(S = \emptyset \)
+ Với \(a > 0:S = \left\{ {\frac{{a - 1}}{{2a}}} \right\}\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 24 trang 84 SGK Toán 10 NC
Bài tập 25 trang 85 SGK Toán 10 NC
Bài tập 27 trang 85 SGK Toán 10 NC
Bài tập 28 trang 85 SGK Toán 10 NC
Bài tập 29 trang 85 SGK Toán 10 NC
Bài tập 33 trang 94 SGK Toán 10 NC
Bài tập 34 trang 94 SGK Toán 10 NC
Bài tập 35 trang 94 SGK Toán 10 NC
Bài tập 36 trang 96 SGK Toán 10 NC
Bài tập 37 trang 97 SGK Toán 10 NC
Bài tập 38 trang 97 SGK Toán 10 NC
Bài tập 39 trang 97 SGK Toán 10 NC
Bài tập 40 trang 97 SGK Toán 10 NC
Bài tập 41 trang 97 SGK Toán 10 NC
Bài tập 42 trang 97 SGK Toán 10 NC
Bài tập 43 trang 97 SGK Toán 10 NC
Bài tập 44 trang 97 SGK Toán 10 NC
Bài tập 45 trang 100 SGK Toán 10 NC
Bài tập 46 trang 100 SGK Toán 10 NC
Bài tập 47 trang 100 SGK Toán 10 NC
-


Giải và biện luận căn(x+m)-căn(x-m)=m
bởi Nguyễn Trường Giang
 09/11/2019
Giải giúp mình mấy câu này với.Khó quá
09/11/2019
Giải giúp mình mấy câu này với.Khó quá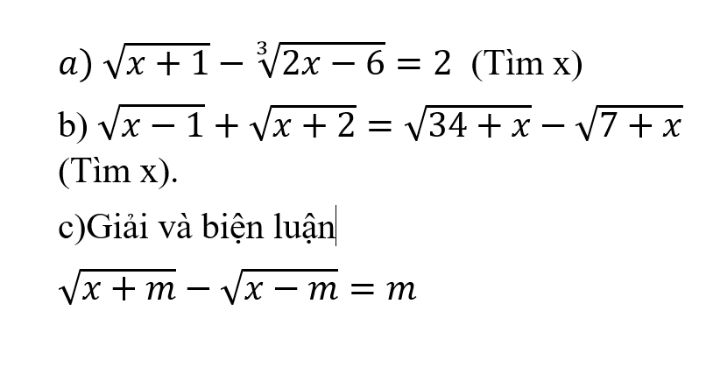 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải hệ phương trình x^2+y^2=13 và 3(x+y)+2xy+9=0
bởi Dololo Trần
 23/10/2019
23/10/2019
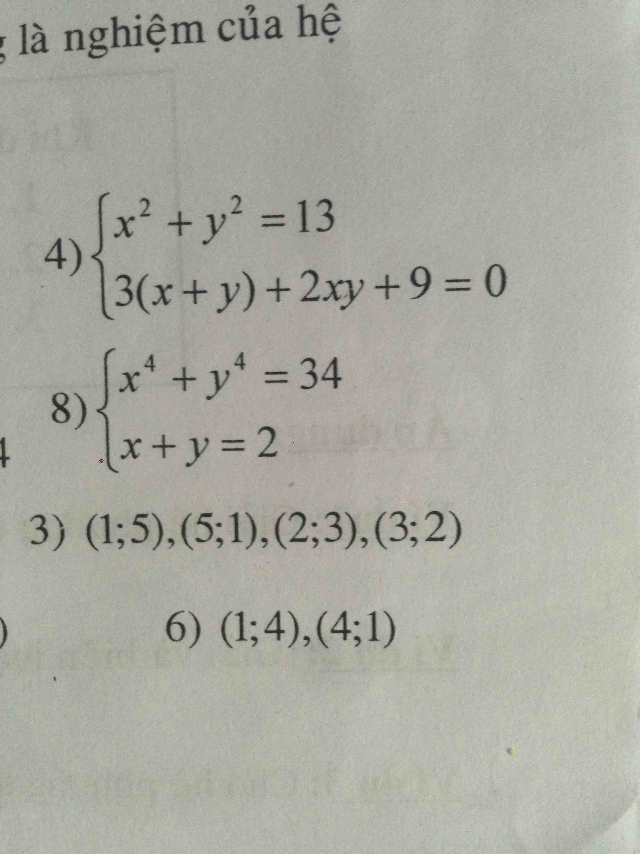 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Giải phương trình căn ((x+1)(2-x))=1+2x-2x^2
bởi Khánh Linh
 07/12/2018
07/12/2018
Giải phương trình căn ((x+1)(2-x))=1+2x-2x^2
Theo dõi (0) 2 Trả lời -


Giải phương trình x+căn(17-x^2)+x căn(17-x^2)=9
bởi Trần Trọng
 22/10/2018
22/10/2018
Giải phương Trình
a)
b)
Theo dõi (0) 1 Trả lời -
ADMICRO


Giải hệ phương trình 3x+y=1/x^2 và 3y+x=1/y^2
bởi Co Nan
 13/10/2018
13/10/2018
giải hệ pt: \(\left\{{}\begin{matrix}3x+y=\dfrac{1}{x^2}\\3y+x=\dfrac{1}{y^2}\end{matrix}\right.\)
Theo dõi (0) 1 Trả lời





