Giải bài 1.18 tr 21 SBT Hình học 10
Cho hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) có điểm đặt O và tạo với nhau góc 600. Tìm cường độ tổng hợp lực của hai lực ấy biết rằng cường độ của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đều là 100N.
Hướng dẫn giải chi tiết
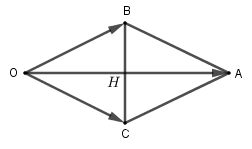
\(\overrightarrow {{F_1}} + {\overrightarrow F _2} = \overrightarrow F = \overrightarrow {OA} \Rightarrow \left| {\overrightarrow {{F_1}} + {{\overrightarrow F }_2}} \right| = OA\)
Xét hình bình hành OBAC có OB = OC = 100 nên là hình thoi.
⇒ OA ⊥ B tại H.
Mà \(\widehat {BOC} = {60^0}\) nên tam giác BOC đều và \(OH = \sqrt {O{B^2} - B{H^2}} = \sqrt {{{100}^2} - {{50}^0}} = 50\sqrt 3 \).
Vậy cường độ của hợp lực là \(OA = 2OH = 100\sqrt 3 N\).
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 1.16 trang 21 SBT Hình học 10
Bài tập 1.17 trang 21 SBT Hình học 10
Bài tập 1.19 trang 21 SBT Hình học 10
Bài tập 6 trang 14 SGK Hình học 10 NC
Bài tập 7 trang 14 SGK Hình học 10 NC
Bài tập 8 trang 14 SGK Hình học 10 NC
Bài tập 9 trang 14 SGK Hình học 10 NC
Bài tập 10 trang 14 SGK Hình học 10 NC
Bài tập 11 trang 14 SGK Hình học 10 NC
Bài tập 12 trang 14 SGK Hình học 10 NC
Bài tập 13 trang 15 SGK Hình học 10 NC
Bài tập 14 trang 17 SGK Hình học 10 NC
Bài tập 15 trang 17 SGK Hình học 10 NC
Bài tập 16 trang 17 SGK Hình học 10 NC
Bài tập 17 trang 17 SGK Hình học 10 NC
Bài tập 18 trang 17 SGK Hình học 10 NC
-
Bài 1.19 trang 23 sách bài tập Hình học 10
bởi hà trang
02/10/2018
Bài 1.19 (STB trang 23)Cho hình bình hành ABCD. Gọi O là một điểm bất kì trên đường chéo AC. Qua O kẻ các đường thẳng song song với các cạnh của hình bình hành. Các đường thẳng này cắt AB và DC lần lượt tại M và N, cắt AD và BC lần lượt tại E và F. Chứng minh rằng :
a) \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
b) \(\overrightarrow{BD}=\overrightarrow{ME}+\overrightarrow{FN}\)
Theo dõi (0) 1 Trả lời -
Bài 1.18 trang 23 sách bài tập Hình học 10
bởi Đan Nguyên
02/10/2018
Bài 1.18 (STB trang 23)Cho hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) có điểm đặt O vào tạo với nhau góc \(60^0\). Tìm cường độ tổng lực của hai lực ấy biết rằng cường độ của hai lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_2}\) đều là 100N
Theo dõi (0) 1 Trả lời -
Bài 1.17 trang 23 sách bài tập Hình học 10
bởi Lê Vinh
02/10/2018
Bài 1.17 (STB trang 23)Cho 3 điểm O, A, B không thẳng hàng. Với điều kiện nào thì vectơ \(\overrightarrow{OA}+\overrightarrow{OB}\) nằm trên đường phân giác của góc \(\widehat{AOB}\) ?
Theo dõi (0) 1 Trả lời
