Bài tập 12 trang 14 SGK Hình học 10 NC

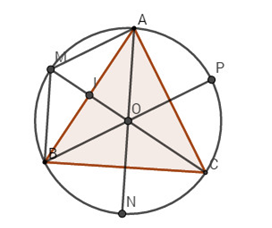
a) Theo quy tắc hình bình hành, ta có AOBM là hình bình hành.

Ta có AB, OM cắt nhau tại trung điểm mỗi đường, gọi I là trung điểm AB thì OI = IM. O là trọng tâm tam giác ABC nên OC = 2OI = OM.

Do đó O là trung điểm của MC, tức là MC là đường kính của đường tròn.

Vậy điểm M là điểm sao cho CM là đường kính của đường tròn tâm O.

Tương tự, ta cũng có N, P thuộc đường tròn (O) sao cho AN, BP là đường kính của đường tròn (O).

b) O là trung điểm của MC

Nên \(\overrightarrow {OM}  + \overrightarrow {OC}  = \overrightarrow 0 \)

Mà \(\overrightarrow {OM}  = \overrightarrow {OA}  + \overrightarrow {OB} \)

Suy ra \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow 0 \)

-- Mod Toán 10 HỌC247