Bài tập 10 trang 14 SGK Hình học 10 NC
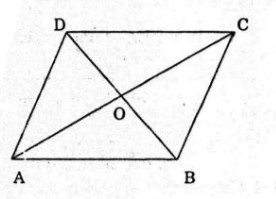
Cho hình bình hành ABCDABCD với tâm O. Hãy điền vào chỗ trống (…) để được đẳng thức đúng
\(\begin{array}{l}
a)\overrightarrow {AB} + \overrightarrow {AD} = ...\\
b)\overrightarrow {AB} + \overrightarrow {CD} = ...\\
c)\overrightarrow {AB} + \overrightarrow {OA} = ...\\
d)\overrightarrow {OA} + \overrightarrow {OC} = ...\\
e)\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = ...
\end{array}\)
Hướng dẫn giải chi tiết
a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (quy tắc hình bình hành)
b) \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AB} + \overrightarrow {BA} = \overrightarrow 0 \)
c) \(\overrightarrow {AB} + \overrightarrow {OA} = \overrightarrow {AB} + \overrightarrow {OB} + \overrightarrow {BA} = \overrightarrow {OB} \) (quy tắc 3 điểm)
d) \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \) (vì O là trung điểm của AC)
e)
\(\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \\
= \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right)\\
= \vec 0 + \vec 0 = \vec 0
\end{array}\)
(vì O là trung điểm của AC, BD)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 8 trang 14 SGK Hình học 10 NC
Bài tập 9 trang 14 SGK Hình học 10 NC
Bài tập 11 trang 14 SGK Hình học 10 NC
Bài tập 12 trang 14 SGK Hình học 10 NC
Bài tập 13 trang 15 SGK Hình học 10 NC
Bài tập 14 trang 17 SGK Hình học 10 NC
Bài tập 15 trang 17 SGK Hình học 10 NC
Bài tập 16 trang 17 SGK Hình học 10 NC
Bài tập 17 trang 17 SGK Hình học 10 NC
Bài tập 18 trang 17 SGK Hình học 10 NC
-


Chứng minh vectoOA+vectoOB+vectoOC+vectoOD+vectoOE=vecto0
bởi Ban Mai
 02/10/2018
02/10/2018
cho ngũ giác đều ABCDE tâm O. Chứng minh rằng vectoOA+vectoOB+vectoOC+vectoOD+vectoOE=vecto0
Theo dõi (0) 1 Trả lời -


Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của AB và CD. Nối AF và CE, 2 đường này cắt đường chéo BD lần lượt tại M và N. Chứng minh vectơ DM = vectơ MN = vectơ NB.
Theo dõi (0) 1 Trả lời -


Chứng minh vt CC'=vt A'B+vt B'A biết tam giác ABC và A'B'C' có trùng trọng tâm
bởi Bánh Mì
 02/10/2018
02/10/2018
Cho mình hỏi : Cho tam giác ABC và A'B'C' có trùng trọng tâm. Chứng minh rằng vec tơ CC' = vec tơ A'B + vec tơ B'A
Theo dõi (0) 1 Trả lời





