Phương pháp giải bài tập về cân bằng của vật rắn không có trục quay môn Vật Lý 10 năm 2021-2022

- Xác định và biểu diễn các lực tác dụng lên vật rắn

- Viết điều kiện cân bằng cho vật rắn: \({{\overrightarrow{F}}_{1}}+{{\overrightarrow{F}}_{2}}+...+{{\overrightarrow{F}}_{n}}=0\)            (*)

- Tìm điểm đồng quy của các lực. Nếu các lực không đồng quy thì trượt các lực trên giá của chúng cho đến khi cùng gặp nhau tại một điểm đồng quy I.

- Giải phương trình (*) theo một trong hai cách sau:

Phân tích và tổng hợp lực theo quy tắc hình bình hành. Tìm hợp lực F theo công thức: \

\(\left\{ \begin{align} & F=\sqrt{F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}c\text{os}\alpha } \\ & \alpha =\left( {{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}} \right) \\ \end{align} \right.\)

Chiếu phương trình (*) lên các trục tọa độ để đưa về dạng đại số.

Chú ý:

- Chương động lực học chất điểm khi biểu diễn lực tác dụng lên vật ta có thể xem vật như chất điểm, rồi biểu diễn các lực lên chất điểm đó.

- Chương tĩnh học vật rắn, vật có kích thước đáng kể so với hệ quy chiếu đang xét nên không thể xem vật như chất điểm, do đó khi biểu diễn lực phải biểu diễn lên vật, tại điểm đặt của lực.

Ví dụ 1: Cho bốn lực đồng quy, đồng phẳng như hình vẽ bên. Biết F₁ = 5N, F₂ = 3N, F₃ = 7N, F₄ = 1N. Tìm hợp lực của bốn lực đó.

Hướng dẫn

+ Ta có: \(\overrightarrow{F}={{\overrightarrow{F}}_{1}}+{{\overrightarrow{F}}_{2}}+{{\overrightarrow{F}}_{3}}+{{\overrightarrow{F}}_{4}}=\left( {{\overrightarrow{F}}_{2}}+{{\overrightarrow{F}}_{4}} \right)+\left( {{\overrightarrow{F}}_{1}}+{{\overrightarrow{F}}_{3}} \right)={{\overrightarrow{F}}_{24}}+{{\overrightarrow{F}}_{13}}\)

+  \({{\overrightarrow{F}}_{24}}\,:\left\{ \begin{align} & {{\overrightarrow{F}}_{24}}\,\uparrow \uparrow \,\,{{\overrightarrow{F}}_{2}}\, \\ & {{F}_{24}}={{F}_{2}}-{{F}_{4}}=2N \\ \end{align} \right.\). Với \({{\overrightarrow{F}}_{13}}\,:\left\{ \begin{align} & {{\overrightarrow{F}}_{13}}\,\uparrow \uparrow \,\,{{\overrightarrow{F}}_{3}}\, \\ & {{F}_{13}}={{F}_{3}}-{{F}_{1}}=2N \\ \end{align} \right.\)

+ Vì \({{\overrightarrow{F}}_{24}}\bot {{\overrightarrow{F}}_{13}}\Rightarrow F=\sqrt{F_{13}^{2}+F_{24}^{2}}=2\sqrt{2}\,N\)

Ví dụ 2: Cho ba lực đồng quy cùng nằm trong một mặt phẳng, có độ lớn bằng nhau và từng đôi một làm thành góc 120⁰. Tìm hợp lực của chúng.

Hướng dẫn

+ Ta có: \({{F}_{1}}={{F}_{2}}={{F}_{3}}=a\)

+ Hợp lực: \(\overrightarrow{F}={{\overrightarrow{F}}_{1}}+{{\overrightarrow{F}}_{2}}+{{\overrightarrow{F}}_{2}}={{\overrightarrow{F}}_{12}}+{{\overrightarrow{F}}_{3}}\)

+ Lại có: \(\left\{ \begin{align} & {{F}_{12}}=\sqrt{F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}\text{cos12}{{\text{0}}^{0}}}=a \\ & \text{cos}\left( \widehat{{{F}_{12}}\text{O}{{\text{F}}_{2}}} \right)\text{=}\frac{F_{1}^{2}-\left( F_{2}^{2}+F_{12}^{2} \right)}{-2{{F}_{2}}{{F}_{12}}}=0,5 \\ \end{align} \right.\)

\(\Rightarrow \widehat{{{F}_{12}}\text{O}{{\text{F}}_{2}}}={{60}^{0}}\Rightarrow \widehat{{{F}_{12}}\text{O}{{\text{F}}_{3}}}={{180}^{0}}\)

+ Do đó: \(\overrightarrow{{{F}_{12}}}\uparrow \downarrow \overrightarrow{{{F}_{3}}}\) và cùng độ lớn nên \(\overrightarrow{{{F}_{12}}}+\overrightarrow{{{F}_{3}}}=0\Rightarrow \overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}+\overrightarrow{{{F}_{3}}}=0\)

Ví dụ 3: Một vật có khối lượng m chịu tác dụng của hai lực lực \({{\overrightarrow{F}}_{1}}\) và \({{\overrightarrow{F}}_{2}}\) như hình. Cho biết \({{F}_{1}}=20\sqrt{3}\)N; \({{F}_{2}}=20\)N; \(\alpha ={{30}^{o}}\) là góc hợp bởi \({{\overrightarrow{F}}_{1}}\) với phương thẳng đứng. Tìm m để vật cân bằng.

Hướng dẫn

+ Gọi \(\overrightarrow{P}\) là trọng lực tác dụng lên vật

+ Để vật cân bằng: \({{\overrightarrow{F}}_{1}}+{{\overrightarrow{F}}_{2}}+\overrightarrow{P}=0\)

+ Gọi \(\overrightarrow{F}\) là hợp lực của hai lực \({{\overrightarrow{F}}_{1}}\) và \({{\overrightarrow{F}}_{2}}\).

+ Ta có: \({{\overrightarrow{F}}_{1}}+{{\overrightarrow{F}}_{2}}+\overrightarrow{P}=0\Leftrightarrow \overrightarrow{F}+\overrightarrow{P}=0\Rightarrow \overrightarrow{F}=-\overrightarrow{P}\)

+ Vậy để vật cân bằng thì hợp của hai lực \({{\overrightarrow{F}}_{1}}\) và \({{\overrightarrow{F}}_{2}}\) phải cùng phương, ngược chiều với \(\overrightarrow{P}\). Do đó ta biểu diễn được các lực như hình vẽ.

+ Từ hình vẽ ta có: \(\frac{{{F}_{2}}}{\sin \alpha }=\frac{{{F}_{1}}}{\sin \beta }\) \(\Rightarrow \sin \beta =\frac{{{F}_{1}}.\sin {{30}^{0}}}{{{F}_{2}}}=\frac{\sqrt{3}}{2}\Rightarrow \left( \begin{align} & \beta ={{60}^{0}} \\ & \beta ={{120}^{0}} \\ \end{align} \right.\)

TH1: \(\beta ={{60}^{0}}\Rightarrow {{\widehat{F}}_{1}}={{90}^{o}}\Rightarrow F=\sqrt{F_{1}^{2}+F_{2}^{2}}=40N\Rightarrow P=40N\Rightarrow m=4kg\)

TH2: \(\beta ={{120}^{0}}\Rightarrow {{\widehat{F}}_{1}}={{30}^{o}}\Rightarrow F={{F}_{2}}=20N\Rightarrow P=20N\Rightarrow m=2kg\)

Vậy có hai trường hợp thoả mãn là m = 2kg hoặc m = 4kg

Ví dụ 4: Một vật có khối lượng m = 3 kg treo vào điểm chính giữa của sợi dây AB. Biết AB = 4 m và CD = 10 cm. Tính lực kéo của mỗi nửa sợi dây. Lấy g = 9,8 m/s2.

Hướng dẫn

+ Các lực được biểu diễn như hình vẽ

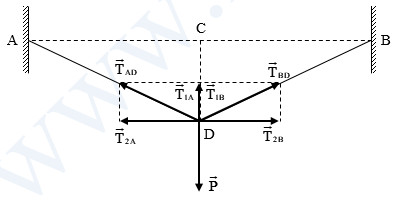
+ Phân tích lực căng của mỗi sợi dây: \(\left\{ \begin{align} & {{\overrightarrow{T}}_{AD}}\,=\,\,{{\overrightarrow{T}}_{1A}}+{{\overrightarrow{T}}_{2A}}\,\,\left( {{\overrightarrow{T}}_{1A}}\uparrow \downarrow \overrightarrow{P},\,{{\overrightarrow{T}}_{2A}}\bot \overrightarrow{P}\, \right)\, \\ & {{\overrightarrow{T}}_{BD}}\,=\,\,{{\overrightarrow{T}}_{1B}}+{{\overrightarrow{T}}_{2B}}\,\,\left( {{\overrightarrow{T}}_{1B}}\uparrow \downarrow \overrightarrow{P},\,{{\overrightarrow{T}}_{2B}}\bot \overrightarrow{P}\, \right) \\ \end{align} \right.\)

Với: \(\left\{ \begin{align} & {{T}_{AD}}={{T}_{BD}}=T \\ & {{T}_{1A}}={{T}_{1B}}={{T}_{1}} \\ & {{T}_{2A}}={{T}_{2B}}={{T}_{2}} \\ \end{align} \right.\)

+ Vì vật nằm cân bằng nên:

\(\overrightarrow{P}+{{\overrightarrow{T}}_{AD}}+{{\overrightarrow{T}}_{BD}}=0\)\(\Leftrightarrow \overrightarrow{P}+{{\overrightarrow{T}}_{1A}}+{{\overrightarrow{T}}_{2A}}+{{\overrightarrow{T}}_{1B}}+{{\overrightarrow{T}}_{2B}}=0\)

+ Vì \(\left\{ \begin{align} & {{\overrightarrow{T}}_{2A}}\uparrow \downarrow {{\overrightarrow{T}}_{2B}} \\ & {{T}_{2A}}={{T}_{2B}} \\ \end{align} \right.\) nên \({{\overrightarrow{T}}_{2A}}+{{\overrightarrow{T}}_{2B}}=0\Rightarrow \overrightarrow{P}+{{\overrightarrow{T}}_{1A}}+{{\overrightarrow{T}}_{1B}}=0\)

+ Mà: \({{\overrightarrow{T}}_{1A}}+{{\overrightarrow{T}}_{1B}}=2\overrightarrow{{{T}_{1}}}\Rightarrow \overrightarrow{P}+2{{\overrightarrow{T}}_{1}}=0\Rightarrow {{T}_{1}}=\frac{P}{2}\Rightarrow {{T}_{1A}}={{T}_{1B}}=\frac{P}{2}\)

+ Từ hình có: \(\sin \alpha =\frac{DC}{\sqrt{A{{C}^{2}}+D{{C}^{2}}}}=\frac{{{T}_{1A}}}{{{T}_{AD}}}=\frac{P}{2T}\Rightarrow T=294N\)

Ví dụ 5: Hai mặt phẳng tạo với mặt nằm ngang các góc 45⁰. Trên hai mặt đó người ta đặt một quả cầu có trọng lượng 20 N. Hãy xác định áp lực của quả cầu lên hai mặt phẳng đỡ.

Hướng dẫn

+ Các lực tác dụng lên quả cầu gồm:

Trọng lực \(\overrightarrow{P}\) có: điểm đặt tại trọng tâm quả cầu, có phương thẳng đứng, có chiều hướng xuống.

Phản lực \({{\overrightarrow{N}}_{1}}\) và \({{\overrightarrow{N}}_{2}}\) của hai mặt phẳng nghiêng có: điểm đặt tại điểm tiếp xúc giữa quả cầu với mặt đỡ, có phương vuông góc với mặt đỡ, có chiều hướng về phía quả cầu.

+ Các lực tác dụng lên quả cầu được biểu diễn như hình vẽ a.

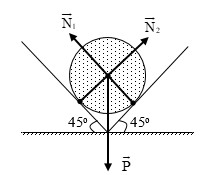
+ Các lực \({{\overrightarrow{N}}_{1}}\), \({{\overrightarrow{N}}_{2}}\) và \(\overrightarrow{P}\) đồng quy tại tâm I của quả cầu nên ta tịnh tiến \({{\overrightarrow{N}}_{1}}\) và \({{\overrightarrow{N}}_{2}}\)lại I  (hình b)

+ Quả cầu nằm cân bằng nên:  \({{\overrightarrow{N}}_{1}}+{{\overrightarrow{N}}_{2}}+\overrightarrow{P}=0\)

+ Gọi \(\overrightarrow{N}\)là lực tổng hợp của hai lực \({{\overrightarrow{N}}_{1}}\) và \({{\overrightarrow{N}}_{2}}\).

\(\Rightarrow \overrightarrow{N}+\overrightarrow{P}=0\Rightarrow N=P=20\left( N \right)\)

+ Vì hai mặt nghiêng tạo với nhau một góc 90^o và N₁ = N₂ nên hình N₁NN_2­I là hình vuông

 \(N={{N}_{1}}\sqrt{2}={{N}_{2}}\sqrt{2}\) \(\Rightarrow {{N}_{1}}={{N}_{2}}=10\sqrt{2}\left( N \right)\)

+ Áp lực \(\overrightarrow{Q}\) cân bằng với phản lực nên áp lực Q do quả cầu đè lên các mặt phẳng nghiêng là: \(Q={{N}_{1}}={{N}_{2}}=10\sqrt{2}\left( N \right)\)

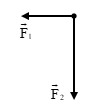
Bài 1: Một vật chịu tác dụng của hai lực \({{\overrightarrow{F}}_{1}}\) và \({{\overrightarrow{F}}_{2}}\) vuông góc với nhau như hình vẽ. Biết \({{F}_{1}}=5N;\text{ }{{F}_{2}}=12N\). Tìm lực \({{\overrightarrow{F}}_{3}}\) tác dụng lên vật để vật cân bằng.

Bài 2: Một vật chịu tác dụng của ba lực \({{\overrightarrow{F}}_{1}}\), \({{\overrightarrow{F}}_{2}}\), \({{\overrightarrow{F}}_{3}}\) như hình vẽ bên thì nằm cân bằng. Biết rằng độ lớn của lực F₃ = \(40\sqrt{3}\)N. Hãy tính độ lớn của lực F₁ và F₂.

Bài 3:Cho ba lực đồng qui (tại điểm O), đồng phẳng \({{\overrightarrow{F}}_{1}},\text{ }{{\overrightarrow{F}}_{2}},\text{ }{{\overrightarrow{F}}_{3}}\) lần lượt hợp với trục Ox những góc \({{0}^{o}},\text{ }{{60}^{o}},\text{ }{{120}^{o}}\) và có độ lớn tương ứng là \({{F}_{1}}={{F}_{3}}=2{{F}_{2}}=10N\) như trên hình vẽ. Tìm hợp lực của ba lực trên.

Bài 4:Hãy dùng quy tắc hình bình hành và quy tắc đa giác lực để tìm hợp lực của ba lực \({{\overrightarrow{F}}_{1}}\), \({{\overrightarrow{F}}_{2}}\) và \({{\overrightarrow{F}}_{3}}\) có độ lớn bằng nhau và bằng F₀. Biết chúng cùng nằm trong cùng một mặt phẳng và \({{\overrightarrow{F}}_{2}}\) làm với hai lực \({{\overrightarrow{F}}_{1}}\) và \({{\overrightarrow{F}}_{3}}\) những góc bằng nhau và bằng 60⁰.

Bài 5:Một chiếc đèn được treo vào tường nhờ một dây AB có không dãn có khối lượng không đáng kể. Muốn cho xa tường, người ta dùng một thanh chống, một đầu tì vào tường, còn đầu kia tì vào điểm B của sợi dây. Biết đèn nặng 40N và dây hợp với tường một góc 45^o. Tính lực căng của dây và phản lực của thanh ?

Bài 6:Một đèn tín hiệu giao thông ba màu được treo ở một ngã tư đường nhờ một dây cáp có trọng lượng không đáng kể. Hai dây cáp được giữ bằng hai cột đèn AB, CD cách nhau 8m. Đèn có khối lượng 6kg được treo vào điểm giữa O của dây cáp, làm dây cáp võng xuống một đoạn 0,5m. Tính lực căng của dây. Lấy g = 10m/s².

Bài 7: Một dây nhẹ căng ngang giữa hai điểm cố định A, B. Treo vào trung điểm O của sợi dây một vật có khối lượng m thì hệ cân bằng, dây hợp với phương ngang góc a. Lấy g = 10 m/s²

a. Tính lực căng dây khi a = 30⁰, m = 10 kg.

b. Khảo sát sự thay đổi độ lớn của lực căng dây theo góc a.

Bài 8: Một chiếc đèn được treo vào tường nhờ một dây AB. Muốn cho đèn ở xa tường, người ta dùng một thanh chống nằm ngang, một đầu tì vào tường, còn đầu kia tì vào điểm B của dây như hình vẽ. Cho biết đèn nặng 4kg và dây hợp với tường một góc 30^o. Tính lực căng của dây và phản lực của thanh. Cho biết phản lực của thanh có phương dọc theo thanh và lấy g = 10 m/s².

Bài 9: Một vật có khối lượng m = 5 kg được treo vào cơ cấu như hình vẽ. Hãy xác định lực do vật nặng m làm căng các dây AC và AB. Lấy g = 10 m/s².

Bài 10: Một ngọn đèn có khối lượng m = 1 kg được treo dưới trần nhà bằng một sợi dây. Dây chỉ chịu được lực căng lớn nhất là 8 N. Lấy g = 9,8 m/s².

a. Chứng minh rằng không thể treo ngọn đèn này vào một đầu dây.

b. Người ta đã treo đèn này bằng cách luồn sợi dây qua một cái móc của đèn và hai đầu dây được gắn chặt lên trần nhà như hình vẽ. Hai nửa sợi dây có chiều dài bằng nhau và hợp với 

---(Nội dung đầy đủ, chi tiết của tài liệu vui lòng xem Online hoặc đăng nhập vào hoc247.net để tải về máy)---

Trên đây là trích dẫn một phần nội dung tài liệu Phương pháp giải bài tập về cân bằng của vật rắn không có trục quay môn Vật Lý 10 năm 2021-2022. Để xem thêm nhiều tư liệu hữu ích khác, các em đăng nhập vào trang hoc247.net để tải tài liệu về máy tính.

Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.

Ngoài ra các em học sinh có thể tham khảo thêm một số tư liệu cùng chuyên mục sau đây:

• Phương pháp giải dạng bài tập về vật rắn có trục quay cố định môn Vật Lý 10 năm 2021-2022