1. KIẾN THỨC CƠ BẢN
Khi giải các bài toán liên quan đến cạnh và đường cao trong tam giác vuông, ngoài việc nắm vững các kiến thức về định lý Talet, về các trường hợp đồng dạng của tam giác, cần phải nắm vững các kiến thức về Hệ thức lượng trong tam giác vuông sau:
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) , ta có:
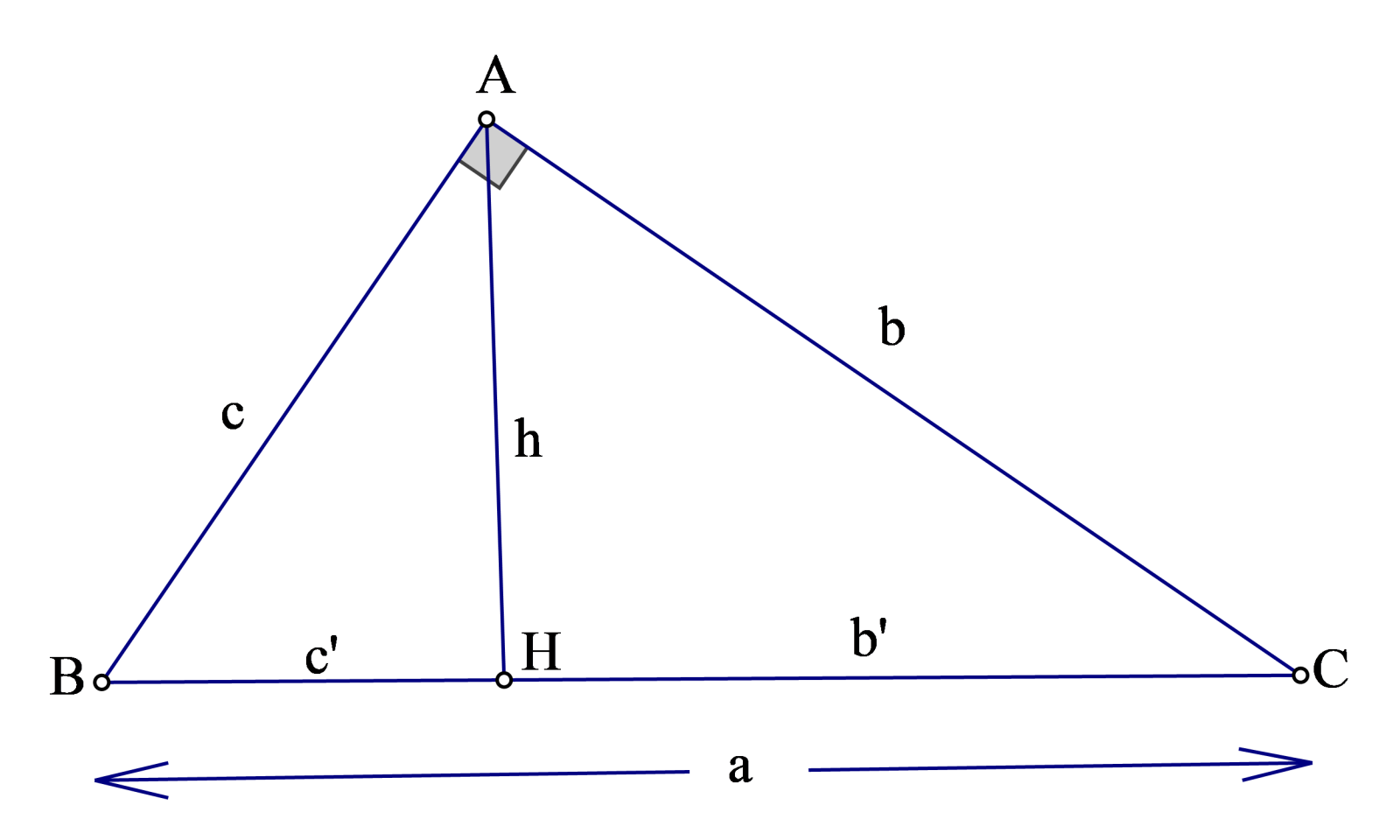
1) \({{a}^{2}}={{b}^{2}}+{{c}^{2}}\)
2) \({{b}^{2}}=a.b';{{c}^{2}}=a.c'\)
3) \({{h}^{2}}=b'.c'\)
4) \(a.h=b.c\)
5) \(\frac{1}{{{h}^{2}}}=\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}\)
6) \(\frac{b'}{a}=\frac{{{b}^{2}}}{{{a}^{2}}}\)
Chú ý: Diện tích tam giác vuông: \(S=\frac{1}{2}ab\)
2. BÀI TẬP ÁP DỤNG
- Ví dụ 1. Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Biết \(AB:AC=3:4\) và \(AB+AC=21cm\).
a) Tính các cạnh của tam giác \(ABC\).
b) Tính độ dài các đoạn \(AH,BH,CH\).
Giải:

a) Theo giả thiết: \(AB:AC=3:4\),
suy ra \(\frac{AB}{3}=\frac{AC}{4}=\frac{AB+AC}{3+4}=3\). Do đó \(AB=3.3=9\)\(\left( cm \right)\); \(AC=3.4=12\left( cm \right)\).
Tam giác \(ABC\) vuông tại \(A\), theo định lý Pythagore ta có:
\(B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}={{9}^{2}}+{{12}^{2}}=225\), suy ra \(BC=15cm\).
b) Tam giác \(ABC\) vuông tại \(A\), ta có \(AH.BC=AB.AC\), suy ra \(AH=\frac{AB.AC}{BC}=\frac{9.12}{15}=7,2\left( cm \right)\).
\(A{{H}^{2}}=BH.HC\). Đặt \(BH=x\left( 0
\({{\left( 7,2 \right)}^{2}}=x\left( 15-x \right)\Leftrightarrow {{x}^{2}}-15x+51,84=0\Leftrightarrow x\left( x-5,4 \right)=9,6\left( x-5,4 \right)=0\)\(\Leftrightarrow \left( x-5,4 \right)\left( x-9,6 \right)=0\Leftrightarrow x=5,4\) hoặc \(x=9,6\) (loại)
Vậy \(BH=5,4cm\). Từ đó \(HC=BC-BH=9,6\left( cm \right)\).
Chú ý: Có thể tính \(BH\) như sau:
\(A{{B}^{2}}=BH.BC\) suy ra \(BH=\frac{A{{B}^{2}}}{BC}=\frac{{{9}^{2}}}{15}=5,4\left( cm \right)\).
- Ví dụ 2: Cho tam giác cân \(ABC\) có đáy \(BC=2a\), cạnh bên bằng \(b\left( b>a \right)\).
a) Tính diện tích tam giác \(ABC\).
b) Dựng \(BK\bot AC\). Tính tỷ số \(\frac{AK}{AC}\).
Giải:
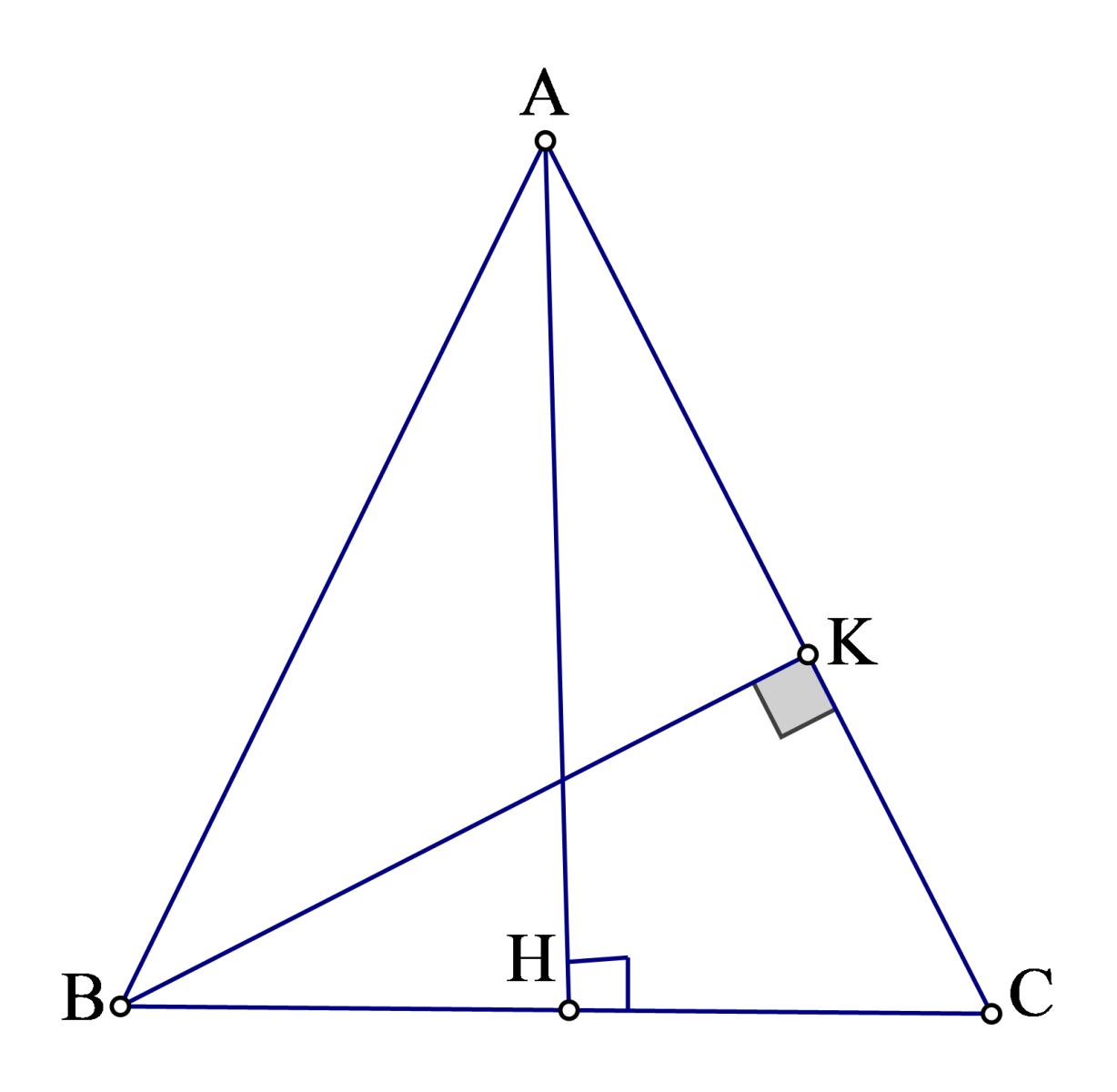
a) Gọi \(H\) là trung điểm của \(BC\). Theo định lý Pitago ta có:
\(A{{H}^{2}}=A{{C}^{2}}-H{{C}^{2}}={{b}^{2}}-{{a}^{2}}\)
Suy ra \({{S}_{ABC}}=\frac{1}{2}BC.AH=\frac{1}{2}a\sqrt{{{b}^{2}}-{{a}^{2}}}\)
\(\Rightarrow AH=\sqrt{{{b}^{2}}-{{a}^{2}}}\)
b) Ta có \(\frac{1}{2}BC.AH=\frac{1}{2}BK.AC={{S}_{ABC}}\)
Suy ra \(BK=\frac{BC.AH}{AC}=\frac{2a}{b}\sqrt{{{b}^{2}}-{{a}^{2}}}\). Áp dụng định lý Pitago trong tam giác vuông \(AKB\) ta có: \(A{{K}^{2}}=A{{B}^{2}}-B{{K}^{2}}={{b}^{2}}-\frac{4{{a}^{2}}}{{{b}^{2}}}\left( {{b}^{2}}-{{a}^{2}} \right)=\frac{{{\left( {{b}^{2}}-2{{a}^{2}} \right)}^{2}}}{{{b}^{2}}}\). Suy ra \(AK=\frac{\left| {{b}^{2}}-2{{a}^{2}} \right|}{b}\) do đó \(\frac{AK}{AC}=\frac{\left| {{b}^{2}}-2{{a}^{2}} \right|}{{{b}^{2}}}\).
- Ví dụ 3: Cho tam giác \(ABC\) với các đỉnh \(A,B,C\) và các cạnh đối diện với các đỉnh tương ứng là: \(a,b,c\).
a) Tính diện tích tam giác \(ABC\) theo \(a\).
b) Chứng minh: \({{a}^{2}}+{{b}^{2}}+{{c}^{2}}\ge 4\sqrt{3}S\).
Giải:
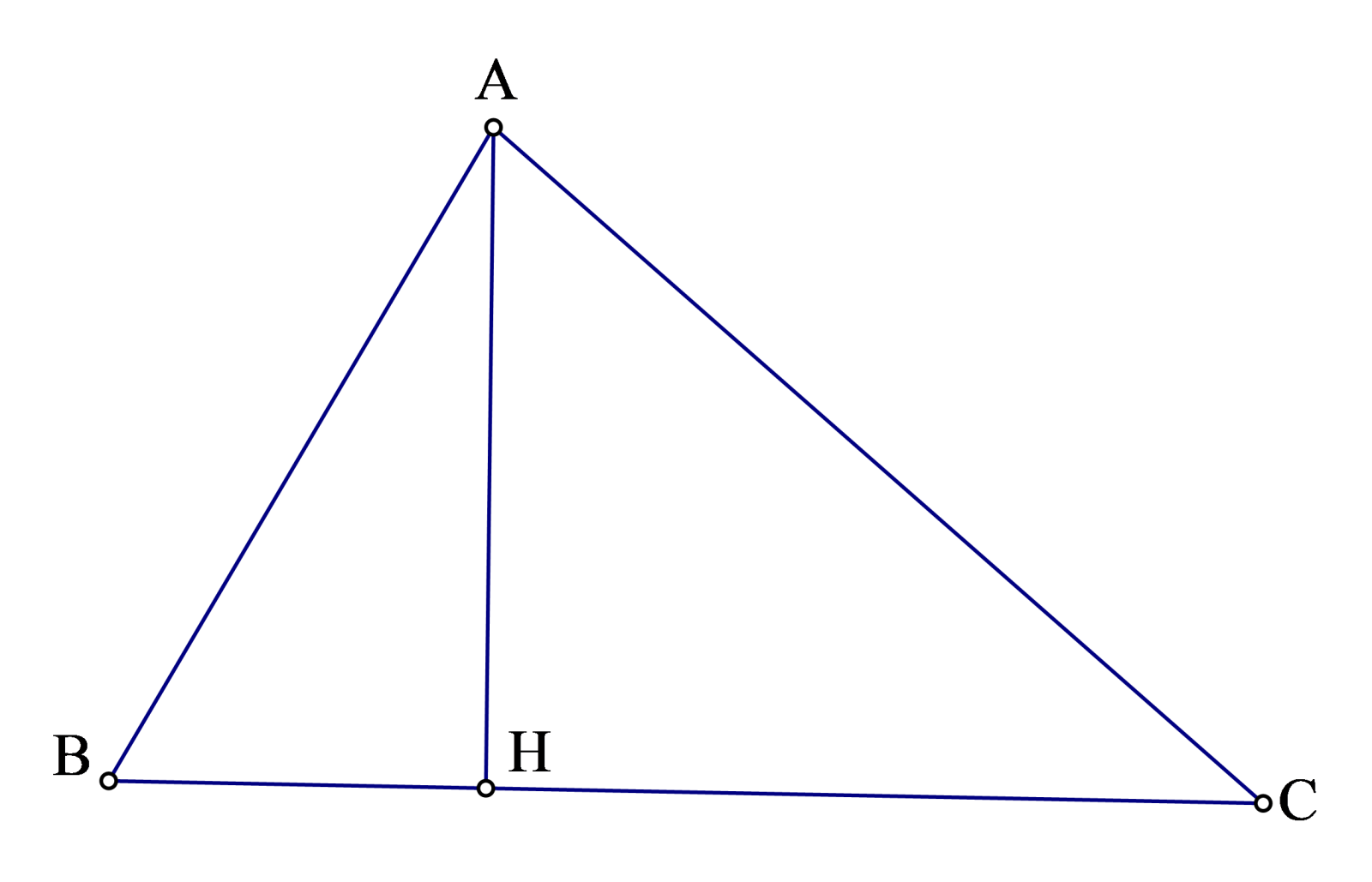
a) Ta giả sử góc \(A\) là góc lớn nhất của tam giác \(ABC\Rightarrow B,C\) là các góc nhọn. Suy ra chân đường cao hạ từ $A$ lên $BC$ là điểm \(H\) thuộc cạnh \(BC\).
Ta có: \(BC=BH+HC\). Áp dụng định lý Pi ta go cho các tam giác vuông \(AHB,AHC\). Ta có: \(A{{B}^{2}}=A{{H}^{2}}+H{{B}^{2}},A{{C}^{2}}=A{{H}^{2}}+H{{C}^{2}}\)
Trừ hai đẳng thức trên ta có:
\({{c}^{2}}-{{b}^{2}}=H{{B}^{2}}-H{{C}^{2}}=\left( HB+HC \right)\left( HB-HC \right)=a.\left( HB-HC \right)\) \(\Rightarrow HB-HC=\frac{{{c}^{2}}-{{b}^{2}}}{a}\)
Ta cũng có: \(HB+HC=a\Rightarrow BH=\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2a}\).
Áp dụng định lý Pitago cho tam giác vuông \(AHB\Rightarrow A{{H}^{2}}={{c}^{2}}-{{\left( \frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2a} \right)}^{2}}=\left( c-\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2a} \right)\left( c+\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2a} \right)\) \(=\left[ \frac{{{\left( a+c \right)}^{2}}-{{b}^{2}}}{2a} \right].\left[ \frac{{{b}^{2}}-{{\left( a-c \right)}^{2}}}{2a} \right]=\frac{\left( a+b+c \right)\left( a+c-b \right)\left( b+a-c \right)\left( b+c-a \right)}{4{{a}^{2}}}\).
Đặt \(2p=a+b+c\) thì \(A{{H}^{2}}=\frac{16p\left( p-a \right)\left( p-b \right)\left( p-c \right)}{4{{a}^{2}}}\Rightarrow AH=2\frac{\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}}{a}\).
Từ đó tính được \(S=\frac{1}{2}BC.AH=\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}\).
b) Từ câu a ta có: \(S=\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}\).
Áp dụng bất đẳng thức Cô si ta có: \(\left( p-a \right)\left( p-b \right)\left( p-c \right)\le {{\left( \frac{p-a+p-b+p-c}{3} \right)}^{3}}=\frac{{{p}^{3}}}{27}\).
Suy ra \(S\le \sqrt{p.\frac{{{p}^{3}}}{27}}=\frac{{{p}^{2}}}{3\sqrt{3}}\).
Hay \(S\le \frac{{{\left( a+b+c \right)}^{2}}}{12\sqrt{3}}\).
Mặt khác ta dễ chứng minh được: \({{\left( a+b+c \right)}^{2}}\le 3\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)\) suy ra \(S\le \frac{3\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)}{12\sqrt{3}}\Leftrightarrow {{a}^{2}}+{{b}^{2}}+{{c}^{2}}\ge 4\sqrt{3}S\)
Dấu bằng xảy ra hki và chỉ khi tam giác \(ABC\) đều.
---(Để xem đầy đủ nội dung chi tiết của tài liệu, các em vui lòng xem online hoặc đăng nhập để tải về máy)---
Trên đây là một phần trích dẫn nội dung Công thức và bài tập áp dụng hệ thức lượng trong tam giác vuông Toán lớp 9 đầy đủ nhất. Để xem toàn bộ nội dung các em đăng nhập vào trang HOC247.net để tải tài liệu về máy tính. Hy vọng tài liệu này sẽ giúp các em học sinh ôn tập tốt và đạt thành tích cao trong học tập.
Chúc các em học tốt!
Tài liệu liên quan
Tư liệu nổi bật tuần
- Xem thêm





