Giải bài tập SGK Bài 4 Chương 3 Hình học 9 Tập 2

Cho đường tròn tâm (O), đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh:

\(\widehat{APO}=\widehat{PBT}\)

Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến A của đường tròn (O') cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O') tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).

Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến kẻ từ A đối với đường tròn (O') cắt (O) tại C đối với đường tròn (O) cắt (O') tại D. Chứng minh rằng:

 \(\widehat{CBA}=\widehat{DBA}\)

Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung, cụ thể là:

Nếu góc BAx (với đỉnh A nằm trên một đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn.

Cho đường tròn (O; R) và dây cung \(BC = R\). Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại A. Tính các góc:

\(\widehat{ABC},\widehat{BAC}\)

Cho đường tròn tâm O đường kính AB. Một tiếp tuyến của đường tròn tại P cắt đường thẳng AB tại T (điểm B nằm giữa O và T).Chứng minh:

\(\widehat{BTP}+ 2.\widehat{TPB}=90^o\)

Cho A, B, C là ba điểm của một đường tròn. At là tiếp  tuyến của đường tròn tại A. Đường thẳng song song với At cắt AB tại M và cắt AC tại N. Chứng minh \(AB. AM = AC . AN\)

Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua điểm M kẻ tiếp tuyến MT và cắt tuyến MAB. Chứng minh \(MT^2 = MA. MB\)

Trên bờ biển có ngọn hải đăng cao 40m. Với khoảng cách bao nhiêu kilomet thì người quan sát trên tàu bắt đầu trông thấy ngọn đèn này biết rằng mắt người quan sát ở độ cao 10 m so với mực nước biển và kính Trái Đất gần bằng 6 400 km (h.30)?

Hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B.\) Qua \(A\) vẽ cát tuyến \(CAD\) với hai đường tròn \((C\in  (O),\) \(D \in (O’)).\)

\(a)\) Chứng minh rằng khi cát tuyến quay xung quang điểm \(A\) thì \(\widehat {CBD}\) có số đo không đổi.

\(b)\) Từ \(C\) và \(D\) vẽ hai tiếp tuyến với đường tròn. Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến \(CAD\) quay xung quanh điểm \(A.\) 

Từ một điểm \(M\) cố định ở bên ngoài đường tròn tâm \(O\) ta kẻ một tiếp tuyến \(MT\) và một cát tuyến \(MAB\) của đường tròn đó.

\(a)\) Chứng minh rằng ta luôn có \(MT^2= MA.MB\) và tích này không phụ thuộc vị trí của cát tuyến \(MAB.\)

\(b)\) Ở hình \(2\) khi cho \(MB =  20 cm,\)\( MB  = 50 cm,\) tính bán kính đường tròn.

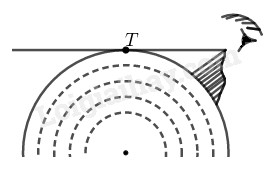
Ngồi trên một đỉnh núi cao \(1km\) thì có thể nhìn thấy một địa điểm \(T\) trên mặt đất với khoảng cách tối đa là bao nhiêu\(?\)  Biết rằng bán kính trái đất gần bằng \(6400km (h.3)\)

Cho tam giác \(ABC\) nội tiếp đường tròn \((O).\) Vẽ tia \(Bx\) sao cho tia \(BC\) nằm giữa hai tia \(Bx;\) \(BA\) và \(\widehat {CBx}= \widehat {BAC}\). Chứng minh rằng \(Bx\) là tiếp tuyến của \((O).\)

Cho đường tròn tâm \(O\) bán kính \(R.\) Lấy ba điểm bất kỳ \(A, B, C\) trên đường tròn \((O).\) Điểm \(E\) bất kỳ thuôc đoạn thẳng \(AB\) (và không trùng với \(A, B\)). Đường thẳng \(d\) đi qua điểm \(E\) và vuông góc với đường thẳng \(OA\) cắt đoạn thẳng \(AC\) tại điểm \(F.\) Chứng minh \(\widehat {BCF} + \widehat {BEF} = {180^o}.\)

Cho tam giác \(ABC\) vuông ở \(A, AH\) và \(AM\) tương ứng là đường cao và đường trung tuyến kẻ từ \(A\) của tam giác đó. Qua điểm \(A\) kẻ đường thẳng \(mn\) vuông góc với \(AM.\) Chứng minh: \(AB\) và \(AC\) tương ứng là tia phân giác của các góc tạo bởi \(AH\) và hai tia \(Am, An\) của đường thẳng \(mn.\)