Bài tập 25 trang 104 SBT Toán 9 Tập 2

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

+) Hai tam giác đồng dạng thì ta có các cạnh tương ứng tỉ lệ.

Lời giải chi tiết

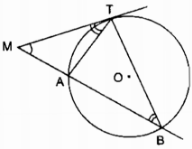
a) Xét ∆MTA và ∆MTB:

Có góc \(\widehat M\) chung

\(\widehat {MTA} = \widehat {TBA}\) (hệ quả góc giữa tia tiếp tuyến và dây)

Hay \(\widehat {MTA} = \widehat {TBM}\)

Suy ra: ∆MAT đồng dạng ∆MTB

\({{MT} \over {MA}} = {{MB} \over {MT}}\)

\( \Rightarrow M{T^2} = MA.MB\)

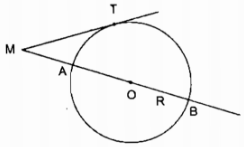
b) Gọi bán kính (O) là R

MB = MA + AB = MA + 2R

\( \Rightarrow MA = MB - 2R\)

\(M{T^2} = MA.MB\)            (chứng minh trên)

\( \Rightarrow M{T^2} = \left( {MB - 2R} \right)MB\)

\( \Rightarrow R = {{M{B^2} - M{T^2}} \over {2MB}}\)

\( = {{2500 - 400} \over {2.50}}\) = 21 (cm)

-- Mod Toán 9 HỌC247