Bài tập 24 tr 103 sách BT Toán lớp 9 Tập 2
Hai đường tròn \((O)\) và \((O’)\) cắt nhau tại \(A\) và \(B.\) Qua \(A\) vẽ cát tuyến \(CAD\) với hai đường tròn \((C\in (O),\) \(D \in (O’)).\)
\(a)\) Chứng minh rằng khi cát tuyến quay xung quang điểm \(A\) thì \(\widehat {CBD}\) có số đo không đổi.
\(b)\) Từ \(C\) và \(D\) vẽ hai tiếp tuyến với đường tròn. Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến \(CAD\) quay xung quanh điểm \(A.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Trong một đường tròn, góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
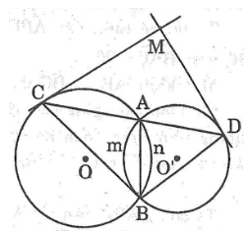
\(a)\) Ta có:
\(\widehat{ACB}=\dfrac{1}{2}sđ \overparen{AnB}\) (góc nội tiếp trong đường tròn \((O))\)
\(\widehat{ADB}=\dfrac{1}{2}sđ \overparen{AmB}\) (góc nội tiếp trong đường tròn \((O'))\)
Vì điểm \(A, B\) cố định nên \(sđ \overparen{AnB},\) \(sđ \overparen{AmB}\) không thay đổi
Vì vậy \(\widehat {ACB},\widehat {ADB}\) có số đo không đổi.
Ta có:\(\widehat {CBD} = {180^o} - \left( {\widehat {ACB} + \widehat {ADB}} \right)\) không đổi do \(\widehat {ACB},\widehat {ADB}\) có số đo không đổi.
Vậy số đo \(\widehat {CBD}\) luôn không đổi khi cát tuyến \(CAD\) thay đổi .
\(b)\) Trong \((O)\) ta có
\(\widehat {ABC} = \widehat {MCA}\) (hệ quả góc giữa tia tiếp tuyến và dây cung) \((1)\)
Trong \((O’)\) ta có: \(\widehat {ABD} = \widehat {MDA}\) (hệ quả góc giữa tia tiếp tuyến và dây cung) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \(\widehat {MCA} + \widehat {MDA} = \widehat {ABC} + \widehat {ABD}\)\( = \widehat {CBD}\)
Hay \(\widehat {MCD} + \widehat {MDC} = \widehat {CBD}\) (không đổi do câu a)
Trong \(∆MCD\) ta có: \(\widehat {CMD} = {180^o} - \left( {\widehat {MCD} + \widehat {MDC}} \right)\)
\(={180^o} - \widehat {CBD}\)
Nên \(\widehat {CMD} \) không đổi do \(\widehat {CBD}\) không đổi.
Vậy \(\widehat {CMD} \) không đổi.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Bài 25 trang 104 sách bài tập toán 9 tập 2
bởi Lê Tường Vy
 10/10/2018
10/10/2018
Bài 25 (Sách bài tập - tập 2 - trang 104)
Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
a) Chứng minh rằng ta luôn có \(MT^2=MA.MB\) và tích này không phụ thuộc vị trí của cát tuyến MAB
b) Ở hình 2, khi cho MT = 20 cm, MB = 50 cm, tính bán kính đường tròn ?
Theo dõi (0) 1 Trả lời -


Bài 24 trang 103 sách bài tập toán 9 tập 2
bởi Ha Ku
 10/10/2018
10/10/2018
Bài 24 (Sách bài tập - tập 2 - trang 103)
Hai đường tròn (O) và (O') cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai đường tròn \(\left(C\in\left(O\right),D\in\left(O'\right)\right)\)
a) Chứng minh rằng khi cát tuyến quay xung quanh điểm A thì \(\widehat{CBD}\) có số đo không đổi
b) Từ C và D vẽ hai tiếp tuyến với đường tròn. Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến CAD quay xung quanh điểm A
Theo dõi (0) 1 Trả lời -


Tìm min A=x^2+xy+y^2-2x-3y+2014
bởi Hoa Hong
 22/02/2019
22/02/2019
Tìm min A=\(x^2+xy+y^2-2x-3y+2014\)
Theo dõi (0) 1 Trả lời





