Bài tập 72 tr 113 sách BT Toán lớp 9 Tập 2
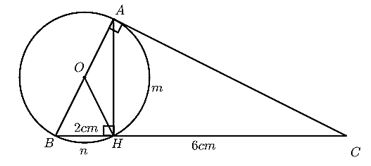
Cho tam giác \(ABC\) vuông ở \(A\) và đường cao \(AH.\) Vẽ đường tròn tâm \(O\) đường kính \(AB.\) Biết \(BH = 2cm\) và \(HC = 6cm.\) Tính:
\(a)\) Diện tích hình tròn \((O).\)
\(b)\) Tổng diện tích hai hình viên phân \(AmH\) và \(BnH\) (ứng với các cung nhỏ).
\(c)\) Diện tích hình quạt tròn \(AOH\) (ứng với cung nhỏ \(AH\)).
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong tam giác vuông, bình phương một cạnh góc vuông bằng tích cạnh huyền với hình chiếu của cạnh góc vuông đó trên cạnh huyền.
+) Diện tích \(S\) của một hình tròn bán kính \(R\) được tính theo công thức: \(S=\pi.R^2\)
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
Lời giải chi tiết
\(a)\) \(∆ABC\) có \(\widehat A = {90^0}\)
Theo hệ thức lượng trong tam giác vuông ta có:
\(A{B^2} = BH.BC \)\(\Rightarrow A{B^2} = 2.\left( {2 + 6} \right) = 16\)
Suy ra \(AB = 4\, (cm)\)
Diện tích hình tròn tâm \(O\) là:
\(S = \displaystyle \pi {\left( {{{AB} \over 2}} \right)^2} \)\(= \displaystyle \pi {\left( {{4 \over 2}} \right)^2} = 4\pi \) \( (cm^2)\)
\(b)\) Trong tam giác vuông \(ABC\) ta có:
\(A{H^2} = HB.HC = 2.6 = 12\)
Suy ra \(AH = 2\sqrt 3 \) \((cm)\)
\(S_{\Delta AHB}= \displaystyle {1 \over 2}AH.BH \)\(= \displaystyle {1 \over 2}.2.2\sqrt 3 = 2\sqrt 3 \) \( (cm^2)\)
Tổng diện tích hai hình viên phân \(AmH\) và \(BnH\) bằng diện tích nửa hình tròn tâm \(O\) trừ diện tích \(∆AHB\) nên tổng diện tích hai hình viên phân là:
\(S = 2\pi - 2\sqrt 3 = 2\left( {\pi - \sqrt 3 } \right)\) \( (cm^2)\)
\(c)\) \(∆BOH\) có \(OB = OH = BH = 2 cm\)
\( \Rightarrow \Delta BOH\) đều
\( \Rightarrow \widehat B = {60^0}\)
\(\widehat B = \displaystyle {1 \over 2} sđ \overparen{AmH}\) (tính chất góc nội tiếp)
\( \Rightarrow sđ \overparen{AmH}\) \( = 2\widehat B = {120^0}\)
\(S_{qAOH}=\displaystyle {{\pi {{.2}^2}.120} \over {360}} = \displaystyle {{4\pi } \over 3}\) \( (cm^2)\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Tính diện tích hoa bốn cánh
bởi Nguyễn Quang Minh Tú
 08/09/2017
08/09/2017
mọi người giải giúp mình bài này với ạ
Cho hình vuông ABCD cạnh là 3 cm, dựng các cung tròn như hình vé tính diện tích của phần hoa 4 cánh được tạo thành(phần màu xanh)
.png) Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời