Bài tập 70 tr 112 sách BT Toán lớp 9 Tập 2
Cho tam giác \(ABC\) nội tiếp đường tròn \((O; R)\) có \(\widehat C = {45^\circ}\).
\(a)\) Tính diện tích hình quạt tròn \(AOB\) (ứng với cung nhỏ \(AB\))
\(b)\) Tính diện tích hình viên phân \(AmB\) (ứng với cung nhỏ \(AB\))
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức: Diện tích hình quạt tròn bán kính \(R,\) cung \(n^\circ\) được tính theo công thức: \(S=\dfrac{\pi R^2n}{360}\).
Lời giải chi tiết
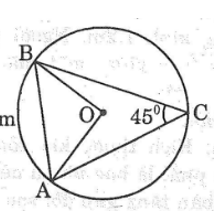
\(a)\) Xét đường tròn \((O)\) có \(\widehat C = {45^\circ }\) \((gt)\) là góc nội tiếp chắn \(\overparen{AmB} \)
\( \Rightarrow sđ \overparen{AmB}= 2.\widehat C\)\(=2.45^0= {90^\circ}\)
Diện tích hình quạt \(AOB\) là:
\(S =\displaystyle {{\pi {R^2}.90} \over {360}} =\displaystyle {{\pi {R^2}} \over 4}\) (đơn vị diện tích)
\(b)\) \(\widehat {AOB} = sđ \overparen{AmB} = {90^0}\)
\( \Rightarrow OA \bot OB\)
Diện tích tam giác \(OAB\) là: \(S =\displaystyle {1 \over 2}OA.OB = \displaystyle {{{R^2}} \over 2}\)
Diện tích hình viên phân \(AmB\) là:
\(S_{qAOB}-S_{AOB}=\displaystyle {{\pi {R^2}} \over 4} - {{{R^2}} \over 2}\)\( =\displaystyle {{{R^2}\left( \displaystyle {\pi - 2} \right)} \over 4}\) (đơn vị diện tích)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Tính diện tích hình tròn biết chu vi của nó là C
bởi Nguyễn Minh Hải
 08/10/2018
08/10/2018
Bài 65 (Sách bài tập - tập 2 - trang 111)
Tính diện tích hình tròn biết chu vi của nó là C ?
Theo dõi (0) 2 Trả lời





