PhαΚßn hΤΑαΜ¦ng dαΚΪn giαΚΘi bΟ†i tαΚ≠p ToΟΓn 8 ChΟΔn trαΜùi sΟΓng tαΚΓo ChΤΑΤΓng 8 BΟ†i 2 CΟΓc trΤΑαΜùng hαΜΘp ΡëαΜ™ng dαΚΓng cαΜßa hai tam giΟΓc sαΚΫ giΟΚp cΟΓc em nαΚ·m ΡëΤΑαΜΘc phΤΑΤΓng phΟΓp vΟ† rΟ®n luyαΜ΅n kΡ© nΡÉng, giαΚΘi bΟ†i tαΚ≠p tαΜΪ SGK ToΟΓn 8 TαΚ≠p 2 ChΟΔn trαΜùi sΟΓng tαΚΓo.
-
KhαΜüi ΡëαΜông trang 67 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
CΟΓc trΤΑαΜùng hαΜΘp ΡëαΜ™ng dαΚΓng cαΜßa hai tam giΟΓc cΟ≥ ΡëiαΜ¹u gΟ§ khΟΓc vαΜ¦i cΟΓc trΤΑαΜùng hαΜΘp bαΚ±ng nhau cαΜßa hai tam giΟΓc?
-
KhΟΓm phΟΓ 1 trang 67 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
Cho tam giΟΓc ABC vΟ† tam giΟΓc A'B'C' cΟ≥ cΟΓc kΟ≠ch thΤΑαΜ¦c nhΤΑ HΟ§nh 1. TrΟΣn cαΚΓnh AB vΟ† AC cαΜßa tam giΟΓc ABC lαΚßn lΤΑαΜΘt lαΚΞy hai ΡëiαΜÉm M, N sao cho AM = 2 cm, AN = 3 cm.
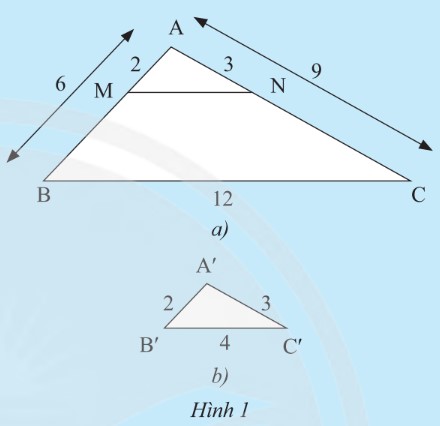
a) So sΟΓnh cΟΓc tαΜâ sαΜë \(\frac{A'B'}{AB},\frac{A'C'}{AC},\frac{B'C'}{BC}\)?
b) TΟ≠nh ΡëαΜô dΟ†i ΡëoαΚΓn thαΚ≥ng MN?
c) Em cΟ≥ nhαΚ≠n xΟ©t gΟ§ vαΜ¹ mαΜëi quan hαΜ΅ giαΜ·a cΟΓc tam giΟΓc ABC, AMN vΟ† A'B'C'?
-
ThαΜ±c hΟ†nh 1 trang 68 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
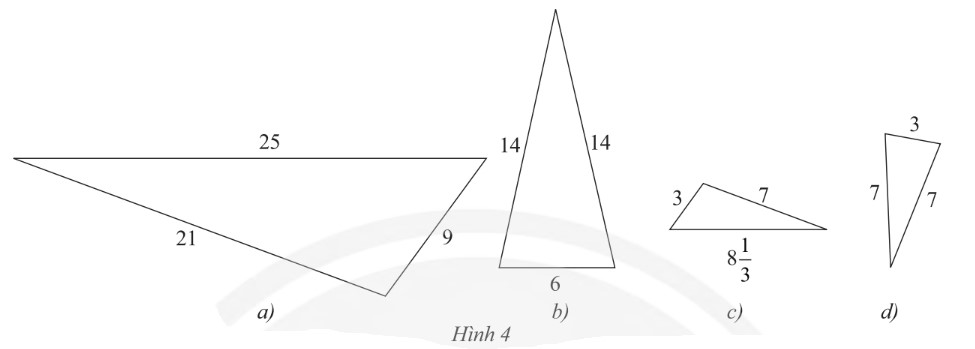
TΟ§m trong HΟ§nh 4 cΟΓc cαΚΖp tam giΟΓc ΡëαΜ™ng dαΚΓng?
-
KhΟΓm phΟΓ 2 trang 68 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
Cho tam giΟΓc DEF vΟ† ABC cΟ≥ \(DE=\frac{1}{3}AB, DF=\frac{1}{3}AC,\widehat{D}=\widehat{A}\) (HΟ§nh 5). TrΟΣn tia AB, lαΚΞy ΡëiαΜÉm M sao cho \(AM = DE\). Qua M kαΚΜ MN // BC (\(N\in AC\)).
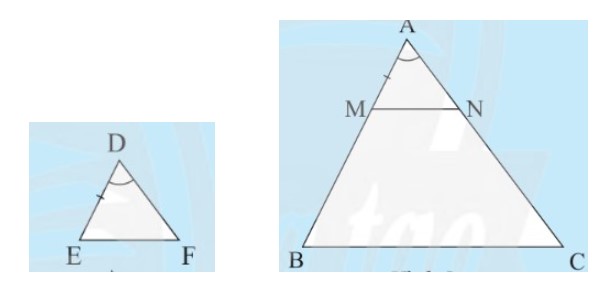
a) So sΟΓnh cΟΓc tαΜâ sαΜë \(\frac{AM}{AB}\) vΟ† \(\frac{AN}{AC}\)?
b) So sΟΓnh AN vΟ† DF?
c) Tam giΟΓc AMN cΟ≥ ΡëαΜ™ng dαΚΓng vαΜ¦i tam giacsc ABC khΟ¥ng?
d) DαΜ± ΡëoΟΓn sαΜ± ΡëαΜ™ng dαΚΓng cαΜßa hai tam giΟΓc DEF vΟ† ABC?
- VIDEOYOMEDIA
-
ThαΜ±c hΟ†nh 2 trang 69 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
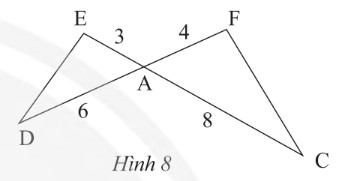
Cho tam giΟΓc ADE vΟ† tam giΟΓc ACF cΟ≥ cΟΓc kΟ≠ch thΤΑαΜ¦c nhΤΑ trong HΟ§nh 8.
ChαΜ©ng minh rαΚ±ng \(\Delta ADEαîï\Delta ACF\)?
-
KhΟΓm phΟΓ 3 trang 69 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
Cho hai tam giΟΓc ABC vΟ† A'B'C' cΟ≥ \(\widehat{A}=\widehat{A'},\widehat{C}=\widehat{C'}\) (HΟ§nh 9).
TrΟΣn cαΚΓnh AC, LαΚΞy ΡëiαΜÉm D sao cho DC = A'C'. Qua D kαΚΜ ΡëΤΑαΜùng thαΚ≥ng song song vαΜ¦i AB cαΚ·t cαΚΓnh BC tαΚΓi E.
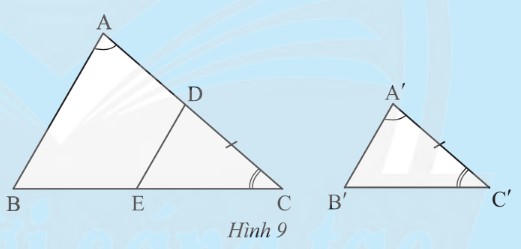
a) Tam giΟΓc DEC cΟ≥ ΡëαΜ™ng dαΚΓng vαΜ¦i tam giΟΓc ABC khΟ¥ng?
b) NhαΚ≠n xΟ©t vαΜ¹ mαΜëi quan hαΜ΅ giαΜ·a tam giΟΓc A'B'C' vΟ† tam giΟΓc DEC?
c) DαΜ± ΡëoΟΓn vαΜ¹ sαΜ± ΡëαΜ™ng dαΚΓng cαΜßa hai tam giΟΓc A'B'C' vΟ† ABC?
-
ThαΜ±c hΟ†nh 3 trang 70 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
Quan sΟΓt HΟ§nh 12.
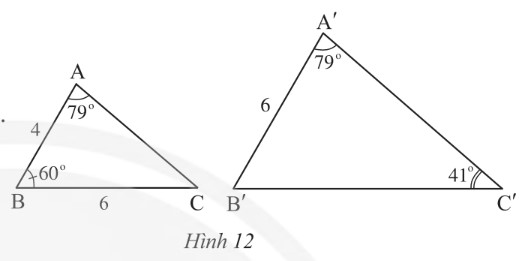
a) ChαΜ©ng minh rαΚ±ng ΈîABCαîïΈîAβÄ≤BβÄ≤CβÄ≤?
b) TΟ≠nh ΡëαΜô dΟ†i B'C'?
-
VαΚ≠n dαΜΞng 1 trang 70 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
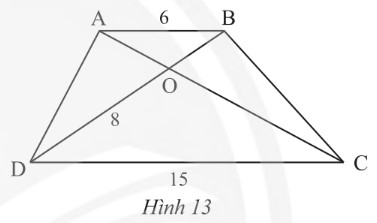
Cho hΟ§nh thang ABCD (AB // CD) cΟ≥ AB = 6m, CD = 15 m, OD = 8 m (HΟ§nh 13). TΟ≠nh ΡëαΜô dΟ†i ΡëoαΚΓn thαΚ≥ng OB?
-
VαΚ≠n dαΜΞng 2 trang 70 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
Qua cΟΓc trΤΑαΜùng hαΜΘp ΡëαΜ™ng dαΚΓng cαΜßa hai tam giΟΓc, hΟΘy trαΚΘ lαΜùi cΟΔu hαΜèi αΜü phΟΔΧÄn KhαΜüi ΡëαΜông (trang 67)?
-
BΟ†i tαΚ≠p 1 trang 70 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
TrΤΑαΜùng hαΜΘp ΡëαΜ™ng dαΚΓng thαΜ© nhαΚΞt (c.c.c)
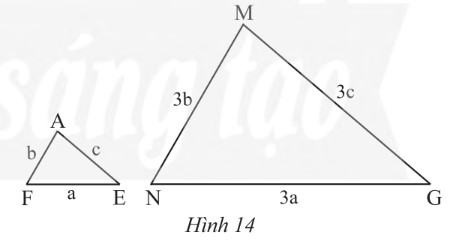
a) Tam giΟΓc AFE vΟ† MNG αΜü HΟ§nh 14 cΟ≥ ΡëαΜ™ng dαΚΓng vαΜ¦i nhau khΟ¥ng? VΟ§ sao?
b) BiαΚΩt tam giΟΓc AFE cΟ≥ chu vi bαΚ±ng 15 cm. TΟ≠nh chu vi tam giΟΓc MNG?
-
BΟ†i tαΚ≠p 2 trang 70 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
Tam giΟΓc ABC cΟ≥ ΡëαΜô dΟ†i \(AB = 4 cm, AC = 6 cm, BC = 9 cm\). Tam giΟΓc A'B'C' ΡëαΜ™ng dαΚΓng vαΜ¦i tam giΟΓc ABC vΟ† cΟ≥ chu vi bαΚ±ng 66,5 cm. HΟΘy tΟ≠nh ΡëαΜô dΟ†i cΟΓc cαΚΓnh cαΜßa tam giΟΓc A'B'C'?
-
BΟ†i tαΚ≠p 3 trang 70 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
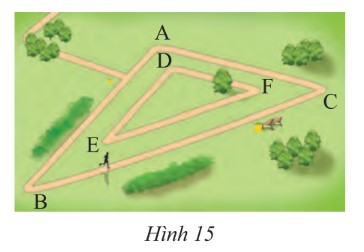
MαΜôt cΟ¥ng viΟΣn cΟ≥ hai ΡëΤΑαΜùng chαΚΓy bαΜô hΟ§nh tam giΟΓc ΡëαΜ™ng dαΚΓng nhΤΑ HΟ§nh 15. KΟ≠ch thΤΑαΜ¦c cαΜßa con ΡëΤΑαΜùng bΟΣn trong lαΚßn lΤΑαΜΘt lΟ† \(300~m, 350~m\) vΟ† \(550~m\). CαΚΓnh ngαΚ·n nhαΚΞt cαΜßa con ΡëΤΑαΜùng bΟΣn ngoΟ†i lΟ† \(660~m\). Nam chαΚΓy bαΜën vΟ≤ng trΟΣn con ΡëΤΑαΜùng bΟΣn trong, HΟΙng chαΚΓy hai vΟ≤ng trΟΣn con ΡëΤΑαΜùng bΟΣn ngoΟ†i. So sΟΓnh quΟΘng ΡëΤΑαΜùng chαΚΓy ΡëΤΑαΜΘc cαΜßa hai bαΚΓn?
-
BΟ†i tαΚ≠p 4 trang 71 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
TrΤΑαΜùng hαΜΘp ΡëαΜ™ng dαΚΓng thαΜ© hai (c.g.c)
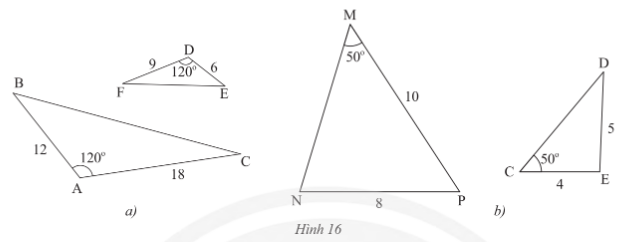
XΟ©t xem cαΚΖp tam giΟΓc nΟ†o trong cΟΓc HΟ§nh 16a, 16b ΡëαΜ™ng dαΚΓng?
-
BΟ†i tαΚ≠p 5 trang 71 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
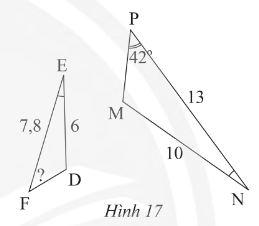
Trong HΟ§nh 17, cho biαΚΩt \(DE = 6~cm, EF= 7,8~cm, NP = 13~cm, NM = 10~cm\), \(\widehat{E}=\widehat{N}\) vΟ† \(\widehat{P}=42^{\circ}\). TΟ≠nh \(\widehat{F}\)?
-
BΟ†i tαΚ≠p 6 trang 71 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
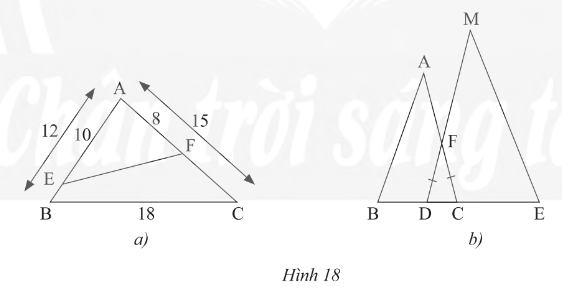
a) Cho tam giΟΓc ABC cΟ≥ AB = 12 cm, AC = 15 cm, BC = 18 cm. TrΟΣn cαΚΓnh AB, lαΚΞy ΡëiαΜÉm E sao cho AE = 10 cm. TrΟΣn cαΚΓnh AC, lαΚΞy ΡëiαΜÉm F sao cho AF = 8 cm (HΟ§nh 18a). TΟ≠nh ΡëαΜô dΟ†i ΡëoαΚΓn thαΚ≥ng EF?
b) Trong HΟ§nh 18b, cho biαΚΩt FD = FC, BC = 9 dm, DE = 12 dm, AC = 15 dm, MD = 20 dm. ChαΜ©ng minh rαΚ±ng ΈîABCαîïΈîMED?
-
BΟ†i tαΚ≠p 7 trang 71 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
Trong HΟ§nh 19, cho biαΚΩt MN // BC, MB // AC.
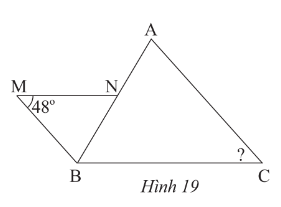
a) ChαΜ©ng minh \(\Delta BNMαîï\Delta ABC\)?
b) TΟ≠nh \(\widehat{C}\)?
-
BΟ†i tαΚ≠p 8 trang 72 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
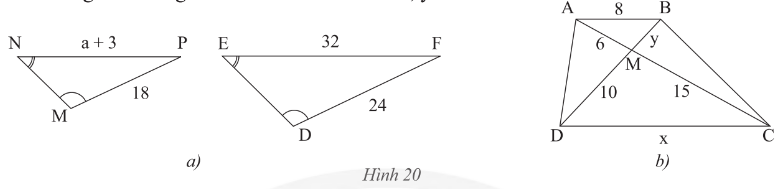
a) Trong HΟ§nh 20a, cho biαΚΩt \(\widehat{N}=\widehat{E},\widehat{M}=\widehat{D}\), MP = 18 m, DF = 24 m, EF = 32 m, NP = a + 3 (m). TΟ§m a?
b) Cho ABCD lφ hϧnh thang (AB // CD) (Hϧnh 20b).
ChαΜ©ng minh rαΚ±ng \(\Delta AMBαîï\Delta CMD\). TΟ§m x, y?
-
BΟ†i tαΚ≠p 9 trang 72 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
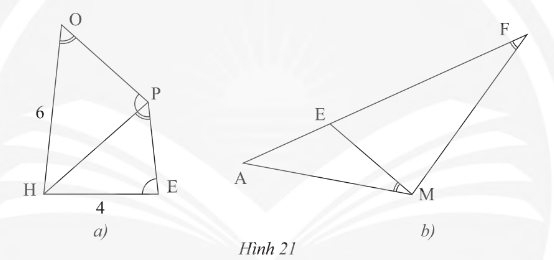
a) Trong HΟ§nh 21a, cho biαΚΩt \(\widehat{HOP}=\widehat{HPE},~\widehat{HPO}=\widehat{HEP},~OH=6~cm\) vΟ† \(HE = 4~cm\). TΟ≠nh ΡëαΜô dΟ†i ΡëoαΚΓn thαΚ≥ng HP?
b) Trong HΟ§nh 21b, cho biαΚΩt \(\widehat{AME}=\widehat{AFM}\). ChαΜ©ng minh rαΚ±ng \(AM^{2}=AE.AF\)?
-
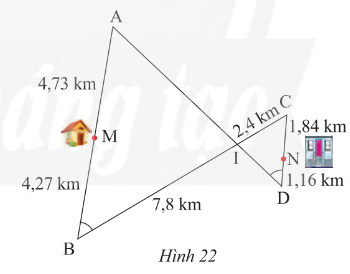
BΟ†i tαΚ≠p 10 trang 72 SGK ToaΧ¹n 8 ChΟΔn trΤΓΧÄi saΧ¹ng taΧΘo TΟΔΧΘp 2 - CTST
ΡêΤΑαΜùng Ρëi vΟ† khoαΚΘng cΟΓch tαΜΪ nhΟ† anh Thanh (ΡëiαΜÉm M) ΡëαΚΩn cΟ¥ng ty (ΡëiαΜÉm N) ΡëΤΑαΜΘc thαΜÉ hiαΜ΅n trong HΟ§nh 22. HΟΘy tΟ§m con ΡëΤΑαΜùng ngαΚ·n nhαΚΞt ΡëαΜÉ Ρëi tαΜΪ nhΟ† cαΜßa anh Thanh ΡëαΚΩn cΟ¥ng ty?